Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T07:01:31.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Statistical properties of particle segregation in homogeneous isotropic turbulence

Published online by Cambridge University Press:  03 October 2011

Elena Meneguz  and
Michael W. Reeks
Elena Meneguz*
Affiliation:
School of Mechanical and Systems Engineering, University of Newcastle, Stephenson Building, Claremont Road, Newcastle upon Tyne NE1 7RU, UK
Michael W. Reeks
Affiliation:
School of Mechanical and Systems Engineering, University of Newcastle, Stephenson Building, Claremont Road, Newcastle upon Tyne NE1 7RU, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A full Lagrangian method (FLM) is used in direct numerical simulations (DNS) of incompressible homogeneous isotropic and statistically stationary turbulent flow to measure the statistical properties of the segregation of small inertial particles advected with Stokes drag by the flow. Qualitative good agreement is observed with previous kinematic simulations (KS) (IJzermans, Meneguz & Reeks, J. Fluid Mech., vol. 653, 2010, pp. 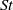99–136): in particular, the existence of singularities in the particle concentration field and a threshold value for the particle Stokes number above which the net compressibility of the particle concentration changes sign (from compression to dilation). A further KS analysis is carried out by examining the distribution in time of the compression of an elemental volume of particles, which shows that it is close to Gaussian as far as the third and fourth moments but non-Gaussian (within the uncertainties of the measurements) for higher-order moments when the contribution of singularities in the tails of the distribution increasingly dominates the statistics. Measurements of the rate of occurrence of singularities show that it reaches a maximum at 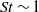, with the distribution of times between singularities following a Poisson process. Following the approach used by Fevrier, Simonin & Squires (J. Fluid Mech., vol. 553, 2005, pp. 1–46), we also measured the random uncorrelated motion (RUM) and mesoscopic components of the compression for 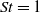and show that the non-Gaussian highly intermittent part of the distribution of the compression is associated with the RUM component and ultimately with the occurrence of singularities. This result is consistent with the formation of caustics (Wilkinson et al. Phys. Fluids, vol. 19, 2007, p. 113303), where the activation of singularities precedes the crossing of trajectories (RUM).

JFM classification

Turbulent Flows: Homogeneous turbulence Multiphase and Particle-laden Flows: Particle/fluid flow Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 686 , 10 November 2011 , pp. 338 - 351
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abou El-Azm Aly, A. & Nicolleau, F. 2008 Dispersion of heavy particle sets in isotropic turbulence using kinematic simulation. Phys. Rev. E 78, 016310.CrossRefGoogle ScholarPubMed
2. Canuto, C., Hussaini, M. Y., Quarteroni, A. & Zang, T. 1991 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
3. Chen, L., Goto, S. & Vassilicos, J. C. 2006 Turbulent clustering of stagnation points and inertial particles. J. Fluid Mech. 553, 143–154.CrossRefGoogle Scholar
4. Coleman, S. W. & Vassilicos, J. C. 2009 A unified sweep-stick mechanism to explain particle clustering in two- and three-dimensional homogeneous isotropic turbulence. Phys. Fluids 21, 113301–113310.CrossRefGoogle Scholar
5. Crowe, C. T., Chung, J. N. & Troutt, T. R. 1993 Particulate Two-Phase Flow, vol. 626. Heinemamm.Google Scholar
6. Ducasse, L. & Pumir, A. 2009 Inertial particle collisions in turbulent synthetic flows: quantifying the sling effect. Phys. Rev. E 80, 066312.CrossRefGoogle ScholarPubMed
7. Falkovich, G. & Pumir, A. 2004 Intermittent distribution of heavy particles in a turbulent flow. Phys. Fluids 16 (7), L47–L50.CrossRefGoogle Scholar
8. Falkovich, G. & Pumir, A. 2007 Sling effect in collisions of water droplets in turbulent clouds. Am. Meteorol. Soc. 64, 4497–4505.Google Scholar
9. Fevrier, P., Simonin, O. & Squires, K. D. 2005 Partitioning of particle velocity in gas–solid turbulent flows into a continuous field and a spatially uncorrelated random distribution; theoretical formalism and numerical study. J. Fluid Mech. 553, 1–46.Google Scholar
10. Goto, S. 2008 A physical mechanism of the energy cascade in homogeneous isotropic turbulence. J. Fluid Mech. 605, 355–366.CrossRefGoogle Scholar
11. Healy, D. P. & Young, J. B. 2005 Full Lagrangian methods for calculating particle concentration fields in dilute gas-particle flows. Proc. R. Soc. Lond. A 461, 2197–2225.Google Scholar
12. IJzermans, R. H. A., Meneguz, E. & Reeks, M. W. 2010 Segregation of particles in incompressible random flows: singularities, intermittency and random uncorrelated motion (RUM). J. Fluid Mech. 653, 99–136.CrossRefGoogle Scholar
13. IJzermans, R. H. A., Reeks, M. W., Meneguz, E., Picciotto, M. & Soldati, A. 2009 Measuring segregation of inertial particles in turbulence by a full Lagrangian approach. Phys. Rev. E 80, 015302.CrossRefGoogle ScholarPubMed
14. Masi, E., Riber, E., Sierra, P., Simonin, O. & Gicquel, L. Y. M. 2010 Modelling the random uncorrelated velocity stress tensor for unsteady particle eulerian simulation in turbulent flows. In 7th International Conference on Multiphase Flows, Tampa, FL. University of Florida.Google Scholar
15. Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.CrossRefGoogle Scholar
16. Monchaux, R., Bourgoin, M. & Cartellier, A. 2010 Preferential concentration of heavy particles: a Voronoï analysis. Phys. Fluids 22, 103304.CrossRefGoogle Scholar
17. Osiptsov, A. N. 2000 Lagrangian modelling of dust admixture in gas flows. Astrophys. Space Sci. 274, 377–386.CrossRefGoogle Scholar
18. Reeks, M. W. 2004 Simulation of particle diffusion, segregation, and intermittency in turbulent flows. In Proceedings of IUTAM Symposium on Computational Modelling of Disperse Multiphase Flow (ed. S. Balachandar & A. Prosperetti) pp. 21–30. Elsevier.CrossRefGoogle Scholar
19. Shaw, R. A. 2003 Particle–turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 35, 183–227.CrossRefGoogle Scholar
20. Taylor, G. I. 1922 Diffusion by continuous movements. Proc. Lond. Math. Soc. s2 20 (1), 196–212.CrossRefGoogle Scholar
21. Wang, L. P. & Maxey, M. R. 1993 Settling velocities and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.CrossRefGoogle Scholar
22. Wilkinson, M. & Mehlig, B. 2005 Caustics in turbulent aerosols. Europhys. Lett. 71, 186–192.CrossRefGoogle Scholar
23. Wilkinson, M., Mehlig, B., Ostlund, S. & Duncan, K. P. 2007 Unmixing in random flows. Phys. Fluids 19, 113303.CrossRefGoogle Scholar