Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-05T15:08:53.770Z Has data issue: false hasContentIssue false
  • English
  • Français

Stationary plume induced by carbon dioxide dissolution

Published online by Cambridge University Press:  19 February 2013

F. Nadal ,
P. Meunier ,
B. Pouligny  and
E. Laurichesse
F. Nadal
Affiliation:
Commissariat à l’Énergie Atomique (CEA), 33314 Le Barp, France
P. Meunier*
Affiliation:
IRPHE UMR 7342, CNRS, Aix Marseille Université, Centrale Marseille, 13013 Marseille, France
B. Pouligny
Affiliation:
CRPP UPR 8641, CNRS, Université Bordeaux I, 33600 Pessac, France
E. Laurichesse
Affiliation:
CRPP UPR 8641, CNRS, Université Bordeaux I, 33600 Pessac, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, laminar convection flows induced by carbon dioxide absorption are addressed from experimental, numerical and theoretical points of view. A vertical glass tube (of centimetre scale) filled with distilled water is subjected to a sudden increase in the partial pressure of carbon dioxide. As a result of the diffusion of the gas into the unsaturated solution, a thin layer of fluid located underneath the surface becomes heavier. This initial density gradient first destabilizes to form a plume, which goes downwards through the entire cell. After a first transient pulsating regime (periodic succession of such Rayleigh–Bénard plumes), a stationary flow settles in the tube, which is maintained by the constant supply of gas at the surface. At late stages, this stationary regime is followed by an aperiodic regime, which lasts until the complete saturation of the solution (thermodynamic equilibrium). The present study only focuses on the stationary regime, whose characteristics appear to be almost independent of the Bond number and the aspect ratio but strongly dependent on the chemical Rayleigh number. Three decades of Rayleigh numbers are explored using particle image velocimetry measurements, which allows for a precise determination of the scaling exponents for the vertical velocity amplitude and the plume width. The assumption that gravity and a constant pressure gradient balance the viscous effects enables us to derive an analytic expression for the stationary vertical velocity on the axis, which scales as 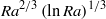${\mathit{Ra}}^{2/ 3} \mathop{(\ln \mathit{Ra})}\nolimits ^{1/ 3} $. As a consequence, the width of the plume scales as 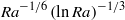${\mathit{Ra}}^{- 1/ 6} \mathop{(\ln \mathit{Ra})}\nolimits ^{- 1/ 3} $ and the mass Nusselt number as 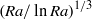$\mathop{(\mathit{Ra}/ \ln \mathit{Ra})}\nolimits ^{1/ 3} $. These scalings are in excellent agreement with the experimental and numerical results. The multiplicative constants of these scalings can also be calculated and show a fairly good agreement if a rigid boundary condition (no-slip) is assumed at the free surface.

JFM classification

Convection: Buoyancy-driven instability Convection: Convection Convection: Plumes/thermals
Type
Papers
Information
Journal of Fluid Mechanics , Volume 719 , 25 March 2013 , pp. 203 - 229
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, E. E., Golomb, D., Zhang, X. Y. & Herzog, H. J. 1995 Confined release of ${\mathrm{CO} }_{2} $ into shallow seawater. In Direct Ocean Disposal of Carbon Dioxide (ed. Handa, N. & Ohsumi, T.), pp. 153–164. Terra Scientific.Google Scholar
Alendal, G., Drange, H. & Haugan, P. M. 1994 Modelling of deep-sea gravity currents using an integrated plume model. In The Polar Oceans and Their Role in Shaping the Global Environment (ed. Johannessen, O. M., Muench, R.D. & Overland, J.E.), pp. 237–246. American Geophysical Union.Google Scholar
Anderson, D. 1975 Chemical plumes in the mantle. Geol. Soc. Am. Bull. 86, 1593–1600.2.0.CO;2>CrossRefGoogle Scholar
Aya, I., Yamane, K. & Shiozaki, K. 1999 Proposal of self sinking ${\mathrm{CO} }_{2} $ sending system: COSMOS. In Greenhouse Gas Control Technologies (ed. Eliasson, B., Riemer, P. W. F. & Wokaun, A.), pp. 269–274. Pergamon.Google Scholar
Batchelor, G. K. 1954 Heat convection and buoyancy effects in fluids. Q. J. R. Meteorol. Soc. 80, 339–358.Google Scholar
Caulfield, J. A. 1996 Environmental impacts of carbon dioxide ocean disposal: plume predictions and time dependent organism experience. Master’s degree report, Massachussets Institute of Technology.Google Scholar
Concus, P. 1968 Static menisci in a vertical right cylinder. J. Fluid Mech. 34, 481–495.Google Scholar
Cussler, E. 1997 Diffusion: Mass Transfer in Fluid Systems. Cambridge University Press.Google Scholar
Dombrowski, C., Lewellyn, B., Pesci, A. I., Restrepo, J. M., Kessler, J. O. & Goldstein, R. E. 2005 Coiling, entrainment, and hydrodynamic coupling of decelerated fluid jets. Phys. Rev. Lett. 95, 184501.Google Scholar
Duda, J. & Vrentas, J. 1971 Steady flow in the region of closed streamlines in a cylindrical cavity. J. Fluid Mech. 45, 247–260.Google Scholar
Frank, M. J. W., Kuipers, J. A. M. & van Swaaij, W. P. M. 1996 Diffusion coefficients of ${\mathrm{CO} }_{2} + {\mathrm{H} }_{2} \mathrm{O} $ , ${\mathrm{CO} }_{2} + {\mathrm{CH} }_{3} \mathrm{OH} , {\mathrm{NH} }_{3} + {\mathrm{H} }_{2} \mathrm{O} $ , and ${\mathrm{NH} }_{3} + {\mathrm{CH} }_{3} \mathrm{OH} $ liquid mixtures. J. Chem. Eng. Data 41, 297–302.CrossRefGoogle Scholar
Fujii, T. 1963 Theory of the steady laminar natural convection above a horizontal line heat source and a point heat source. Intl J. Heat Mass Transfer 6, 597.CrossRefGoogle Scholar
Hebach, A., Oberhof, A. & Dahmen, N. 2004 Density of water $~+ $ carbon dioxide at elevated pressures: measurements and correlation. J. Chem. Eng. Data 49 (5), 950–953.CrossRefGoogle Scholar
List, E. J. 1982 Turbulent jets and plumes. Annu. Rev. Fluid Mech. 14, 189–212.Google Scholar
Lombardi, M., Caulfield, C. P., Cossu, C., Pesci, A. I. & Goldstein, R. E. 2011 Growth and instability of a laminar plume in a strongly stratified environment. J. Fluid Mech. 671, 184–206.Google Scholar
Meunier, P. & Leweke, T. 2003 Analysis and optimization of the error caused by high velocity gradients in particle image velocimetry. Exp. Fluids 35 (5), 408–421.Google Scholar
Morgan, W. 1971 Convection plumes in the lower mantle. Nature 20, 42–43.CrossRefGoogle Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Moses, E., Zocchi, G. & Libchaber, A. 1993 An experimental study of laminar plumes. J. Fluid Mech. 251, 581–601.CrossRefGoogle Scholar
Olson, P., Schubert, G. & Anderson, C. 1993 Structure of axisymmetric mantle plumes. J. Geophys. Res. 98, 6829–6844.Google Scholar
Pera, L. & Gebhart, G. 1971 On the stability of laminar plumes: some numerical solutions and experiments. Intl J. Heat Mass Transfer 14, 975–984.Google Scholar
Pesci, A. I., Porter, M. A. & Goldstein, M. A. 2003 Inertially driven buckling and overturning of jets in a Hele-Shaw cell. Phys. Rev. E 68, 056305.Google Scholar
Roberts, G. O. 1977 Fast viscous convection. Geophys. Astrophys. Fluid Dyn. 8, 197–233.CrossRefGoogle Scholar
Schlien, D. & Boxman, R. 1979 Temperature field measurement in an axisymmetric laminar plume. Phys. Fluids 22, 631–634.CrossRefGoogle Scholar
Schofield, S. P. & Restrepo, J. M. 2010 Stability of planar buoyant jets in stratified fluids. Phys. Fluids 22, 053602.Google Scholar
Turner, J. S. 1969 Buoyant plumes and thermals. Annu. Rev. Fluid Mech. 1, 29–44.Google Scholar
Umemura, A. & Busse, F. H. 1989 Axisymmetric convection at large Rayleigh and infinite Prandtl number. J. Fluid Mech. 208, 459–478.CrossRefGoogle Scholar
Whittaker, R. & Lister, J. 2006a Steady axisymmetric creeping plumes above a planar boundary. Part 1. A point source. J. Fluid Mech. 567, 361–378.Google Scholar
Whittaker, R. & Lister, J. 2006b Steady axisymmetric creeping plumes above a planar boundary. Part 2. A distributed source. J. Fluid Mech. 567, 379–397.Google Scholar
Woods, A. W. 2010 Turbulent plumes in nature. Annu. Rev. Fluid Mech. 42, 391–412.Google Scholar
Worster, M. G. 1986 The axisymmetric laminar plume: asymptotic solution for large Prandtl number. Stud. Appl. Math. 75, 139–152.Google Scholar
Ybert, C. 1998 Stabilisation des mousses aqueuses par des protéines. PhD thesis, Université Louis Pasteur (Strasbourg I).Google Scholar
Yih, C. S. 1951 Free convection due to a point source of heat. In Proceedings of the First U.S. National Congress of Applied Mechanics, pp. 941–947.Google Scholar

Nadal et al. supplementary movie

Temporal evolution of a plume created by carbone dioxide dissolution at the surface with Ra=1.9 106, h=3 and Bo=4.9, corresponding to P=4bars, H=18mm and Rc=6mm. The movie is accelerated 16 times.

Download Nadal et al. supplementary movie(Video)
Video 16.8 MB