Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T11:02:58.199Z Has data issue: false hasContentIssue false
  • English
  • Français

Statics and dynamics of liquid barrels in wedge geometries

Published online by Cambridge University Press:  06 March 2018

Élfego Ruiz-Gutiérrez Open the ORCID record for Élfego Ruiz-Gutiérrez [Opens in a new window] ,
Ciro Semprebon ,
Glen McHale  and
Rodrigo Ledesma-Aguilar Open the ORCID record for Rodrigo Ledesma-Aguilar [Opens in a new window]
Élfego Ruiz-Gutiérrez
Affiliation:
Smart Materials and Surfaces Laboratory, Department of Mathematics, Physics and Electrical Engineering, Ellison Place, Northumbria University, Newcastle upon Tyne, NE1 8ST, UK
Ciro Semprebon
Affiliation:
Smart Materials and Surfaces Laboratory, Department of Mathematics, Physics and Electrical Engineering, Ellison Place, Northumbria University, Newcastle upon Tyne, NE1 8ST, UK
Glen McHale
Affiliation:
Smart Materials and Surfaces Laboratory, Department of Mathematics, Physics and Electrical Engineering, Ellison Place, Northumbria University, Newcastle upon Tyne, NE1 8ST, UK
Rodrigo Ledesma-Aguilar*
Affiliation:
Smart Materials and Surfaces Laboratory, Department of Mathematics, Physics and Electrical Engineering, Ellison Place, Northumbria University, Newcastle upon Tyne, NE1 8ST, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

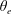We present a theoretical study of the statics and dynamics of a partially wetting liquid droplet, of equilibrium contact angle $\unicode[STIX]{x1D703}_{e}$, confined in a solid wedge geometry of opening angle 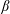$\unicode[STIX]{x1D6FD}$. We focus on a mostly non-wetting regime, given by the condition 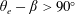$\unicode[STIX]{x1D703}_{e}-\unicode[STIX]{x1D6FD}>90^{\circ }$, where the droplet forms a liquid barrel – a closed shape of positive mean curvature. Using a quasi-equilibrium assumption for the shape of the liquid–gas interface, we compute the changes to the surface energy and pressure distribution of the liquid upon a translation along the symmetry plane of the wedge. Our model is in good agreement with numerical calculations of the surface energy minimisation of static droplets deformed by gravity. Beyond the statics, we put forward a Lagrangian description of the droplet dynamics. We focus on the overdamped limit, where the driving capillary force is balanced by the frictional forces arising from the bulk hydrodynamics, the corner flow near the contact lines and the contact-line friction. Our results provide a theoretical framework to describe the motion of partially wetting liquids in confinement, and can be used to gain further understanding on the relative importance of dissipative processes that span from microscopic to macroscopic length scales.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Contact lines Interfacial Flows (free surface): Liquid bridges
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 842 , 10 May 2018 , pp. 26 - 57
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Al-Housseiny, T. T., Tsai, P. A. & Stone, H. A. 2012 Control of interfacial instabilities using flow geometry. Nat. Phys. 8 (10), 747–750.Google Scholar
Andrews, M. 2006 Alternative separation of Laplace’s equation in toroidal coordinates and its application to electrostatics. J. Electrostat. 64 (10), 664–672.Google Scholar
Baratian, D., Cavalli, A., van den Ende, D. & Mugele, F. 2015 On the shape of a droplet in a wedge: new insight from electrowetting. Soft Matt. 11, 7717–7721.CrossRefGoogle Scholar
Blake, T. D. & Haynes, J. M. 1969 Kinetics of liquid–liquid displacement. J. Colloid Interf. Sci. 30 (3), 421–423.Google Scholar
Bocquet, L. & Charlaix, É. 2010 Nanofluidics, from bulk to interfaces. Chem. Soc. Rev. 39 (3), 1073–1095.Google Scholar
Bocquet, L., Charlaix, É. & Restagno, F. 2002 Physics of humid granular media. C. R. Phys. 3 (2), 207–215.Google Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81 (2), 739–805.CrossRefGoogle Scholar
Brakke, K. A. 1992 The surface evolver. Exp. Maths 1 (2), 141–165.Google Scholar
Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10 (2), 166–188.Google Scholar
Brinkmann, M. & Blossey, R. 2004 Blobs, channels and ‘cigars’: morphologies of liquids at a step. Eur. Phys. J. E 14 (1), 79–89.Google Scholar
Concus, P. & Finn, R. 1969 On the behavior of a capillary surface in a wedge. Proc. Natl Acad. Sci. USA 63 (2), 292.Google Scholar
Concus, P. & Finn, R. 1998 Discontinuous behavior of liquids between parallel and tilted plates. Phys. Fluids 10 (1), 39–43.Google Scholar
Concus, P., Finn, R. & McCuan, J. 2001 Liquid bridges, edge blobs, and Scherk-type capillary surfaces. Indiana Univ. Math. J. 50 (1), 411–441.CrossRefGoogle Scholar
Cox, R. G. 1986 The dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. J. Fluid Mech. 168, 169–194.Google Scholar
Dangla, R., Kayi, S. C. & Baroud, C. N. 2013 Droplet microfluidics driven by gradients of confinement. Proc. Natl Acad. Sci. USA 110 (3), 853–858.Google Scholar
Galley, C. R. 2013 Classical mechanics of nonconservative systems. Phys. Rev. Lett. 110, 174301.CrossRefGoogle ScholarPubMed
de Gennes, P.-G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863.Google Scholar
de Gennes, P.-G., Brochard-Wyart, F. & Quéré, D. 2004 Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls and Waves. Springer.CrossRefGoogle Scholar
Goldstein, H., Poole, C. P. & Safko, J. L. 2001 Classical Mechanics. Addison-Wesley.Google Scholar
Grof, Z., Lawrence, C. J. & Štěpánek, F. 2008 The strength of liquid bridges in random granular materials. J. Colloid Interf. Sci. 319 (1), 182–192.Google Scholar
Hamel, G. 1917 Spiralförmige bewegungen zäher Flüssigkeiten. Jahresbericht der Deutschen Mathematiker-Vereinigung 25, 34–60.Google Scholar
Hauksbee, F. 1710 An account of an experiment touching the direction of a drop of oil of oranges, between two glass planes, towards any side of them that is nearest press’d together. By Mr. Fr. Hauksbee, F. R. S. Phil. Trans. R. Soc. Lond. 27 (325–336), 395–396.Google Scholar
Huh, C. & Scriven, L. E. 1971 Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid Interf. Sci. 35 (1), 85–101.Google Scholar
Jeffery, G. B. 1915 The two-dimensional steady motion of a viscous fluid. Phil. Mag.: Ser. 6 29 (172), 455–465.Google Scholar
Keiser, L., Herbaut, R., Bico, J. & Reyssat, E. 2016 Washing wedges: capillary instability in a gradient of confinement. J. Fluid Mech. 790, 619–633.CrossRefGoogle Scholar
Kohonen, M. M., Geromichalos, D., Scheel, M., Schier, C. & Herminghaus, S. 2004 On capillary bridges in wet granular materials. Physica A 339 (1–2), 7–15.Google Scholar
Kusumaatmaja, H. & Lipowsky, R. 2010 Equilibrium morphologies and effective spring constants of capillary bridges. Langmuir 26 (24), 18734–18741.CrossRefGoogle ScholarPubMed
Landau, L. D. & Lifshitz, E. M. 2013 Fluid Mechanics: Landau and Lifshitz: Course of Theoretical Physics. Elsevier.Google Scholar
Luo, C. & Heng, X. 2014 Separation of oil from a water/oil mixed drop using two nonparallel plates. Langmuir 30 (33), 10002–10010.Google Scholar
Miller, C. A. & Scriven, L. E. 1968 The oscillations of a fluid droplet immersed in another fluid. J. Fluid Mech. 32, 417–435.Google Scholar
Moon, P. & Spencer, D. E. 2012 Field Theory Handbook: Including Coordinate Systems, Differential Equations and their Solutions. Springer.Google Scholar
Morse, P. M. & Feshbach, H. 1953 Methods of Theoretical Physics. McGraw-Hill.Google Scholar
Moulinet, S., Guthmann, C. & Rolley, E. 2002 Roughness and dynamics of a contact line of a viscous fluid on a disordered substrate. Eur. Phys. J. E 8 (4), 437–443.Google ScholarPubMed
Park, C. W., Gorell, S. & Homsy, G. M. 1984 Two-phase displacement in Hele-Shaw cells: experiments on viscously driven instabilities. J. Fluid Mech. 141, 257–287.CrossRefGoogle Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.CrossRefGoogle Scholar
Prakash, M., Quéré, D. & Bush, J. W. M. 2008 Surface tension transport of prey by feeding shorebirds: the capillary ratchet. Science 320 (5878), 931–934.Google Scholar
Ranabothu, S. R., Karnezis, C. & Dai, L. L. 2005 Dynamic wetting: hydrodynamic or molecular-kinetic? J. Colloid Interf. Sci. 288 (1), 213–221.Google Scholar
Renvoisé, P., Bush, J. W. M., Prakash, M. & Quéré, D. 2009 Drop propulsion in tapered tubes. Europhys. Lett. 86 (6), 64003.Google Scholar
Reyssat, E. 2014 Drops and bubbles in wedges. J. Fluid Mech. 748, 641–662.Google Scholar
Rosenhead, L. 1940 The steady two-dimensional radial flow of viscous fluid between two inclined plane walls. Proc. R. Soc. Lond. A 175 (963), 436–467.Google Scholar
de Ruijter, M. J., De Coninck, J. & Oshanin, G. 1999 Droplet spreading: partial wetting regime revisited. Langmuir 15 (6), 2209–2216.Google Scholar
Ruiz-Gutiérrez, É., Guan, J. H., Xu, B., Mchale, G., Wells, G. G. & Ledesma-Aguilar, R. 2017 Energy invariance in capillary systems. Phys. Rev. Lett. 118, 218003.Google Scholar
S̆ikalo, S̆., Tropea, C. & Ganić, E. N. 2005 Dynamic wetting angle of a spreading droplet. Exp. Therm. Fluid Sci. 29 (7), 795–802.Google Scholar
Snoeijer, J. H. 2006 Free-surface flows with large slopes: beyond lubrication theory. Phys. Fluids 18 (2), 021701.CrossRefGoogle Scholar
Snoeijer, J. H. & Andreotti, B. 2013 Moving contact lines: scales, regimes, and dynamical transitions. Annu. Rev. Fluid. Mech. 45, 269–292.Google Scholar
Voinov, O. V. 1976 Hydrodynamics of wetting. Fluid Dyn. 11 (5), 714–721.Google Scholar
Zhong-Can, O.-Y. & Helfrich, W. 1987 Instability and deformation of a spherical vesicle by pressure. Phys. Rev. Lett. 59, 2486–2488.CrossRefGoogle ScholarPubMed