Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Riedinger, Xavier
and
Gilbert, Andrew D.
2014.
Critical layer and radiative instabilities in shallow-water shear flows.
Journal of Fluid Mechanics,
Vol. 751,
Issue. ,
p.
539.
Leclercq, Colin
Nguyen, Florian
and
Kerswell, Rich R.
2016.
Connections between centrifugal, stratorotational, and radiative instabilities in viscous Taylor-Couette flow.
Physical Review E,
Vol. 94,
Issue. 4,
Rüdiger, G.
Seelig, T.
Schultz, M.
Gellert, M.
Egbers, Ch.
and
Harlander, U.
2017.
The stratorotational instability of Taylor-Couette flows with moderate Reynolds numbers.
Geophysical & Astrophysical Fluid Dynamics,
Vol. 111,
Issue. 6,
p.
429.
Park, Junho
Billant, Paul
and
Baik, Jong-Jin
2017.
Instabilities and transient growth of the stratified Taylor–Couette flow in a Rayleigh-unstable regime.
Journal of Fluid Mechanics,
Vol. 822,
Issue. ,
p.
80.
Mougel, J.
Fabre, D.
Lacaze, L.
and
Bohr, T.
2017.
On the instabilities of a potential vortex with a free surface.
Journal of Fluid Mechanics,
Vol. 824,
Issue. ,
p.
230.
Park, Junho
Billant, Paul
Baik, Jong-Jin
and
Seo, Jaemyeong Mango
2018.
Competition between the centrifugal and strato-rotational instabilities in the stratified Taylor–Couette flow.
Journal of Fluid Mechanics,
Vol. 840,
Issue. ,
p.
5.
Wang, Chen
and
Balmforth, Neil J.
2018.
Strato-rotational instability without resonance.
Journal of Fluid Mechanics,
Vol. 846,
Issue. ,
p.
815.
Facchini, Giulio
Favier, Benjamin
Le Gal, Patrice
Wang, Meng
and
Le Bars, Michael
2018.
The linear instability of the stratified plane Couette flow.
Journal of Fluid Mechanics,
Vol. 853,
Issue. ,
p.
205.
Lopez, Juan M.
and
Marques, Francisco
2020.
Impact of centrifugal buoyancy on strato-rotational instability.
Journal of Fluid Mechanics,
Vol. 890,
Issue. ,
Robins, Luke J. M.
Kersalé, Evy
and
Jones, Chris A.
2020.
Viscous and inviscid strato-rotational instability.
Journal of Fluid Mechanics,
Vol. 894,
Issue. ,
Le Gal, P.
Harlander, U.
Borcia, I. D.
Le Dizès, S.
Chen, J.
and
Favier, B.
2021.
Instability of vertically stratified horizontal plane Poiseuille flow.
Journal of Fluid Mechanics,
Vol. 907,
Issue. ,
Park, J.
Prat, V.
Mathis, S.
and
Bugnet, L.
2021.
Horizontal shear instabilities in rotating stellar radiation zones.
Astronomy & Astrophysics,
Vol. 646,
Issue. ,
p.
A64.
Meletti, G.
Abide, S.
Viazzo, S.
Krebs, A.
and
Harlander, U.
2021.
Experiments and long-term high-performance computations on amplitude modulations of strato-rotational flows.
Geophysical & Astrophysical Fluid Dynamics,
Vol. 115,
Issue. 3,
p.
297.
Lopez, Juan M.
and
Marques, Francisco
2022.
Stratified Taylor–Couette flow: nonlinear dynamics.
Journal of Fluid Mechanics,
Vol. 930,
Issue. ,
Labarbe, J.
Le Gal, P.
Harlander, U.
Le Dizès, S.
and
Favier, B.
2023.
Localized layers of turbulence in stratified horizontally sheared Poiseuille flow.
Journal of Fluid Mechanics,
Vol. 963,
Issue. ,
Lopez, Jose M.
Lopez, Juan M.
and
Marques, Francisco
2023.
Stably stratified Taylor–Couette flows.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 381,
Issue. 2246,
Meletti, G.
Abide, S.
Viazzo, S.
and
Harlander, U.
2023.
A parameter study of strato-rotational low-frequency modulations: impacts on momentum transfer and energy distribution.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 381,
Issue. 2246,
Dandoy, V.
Park, J.
Augustson, K.
Astoul, A.
and
Mathis, S.
2023.
How tidal waves interact with convective vortices in rapidly rotating planets and stars.
Astronomy & Astrophysics,
Vol. 673,
Issue. ,
p.
A6.
Khandelwal, Manish K.
Khan, A.
and
Bera, P.
2024.
Modal stability analysis of the density-stratified plane Couette–Poiseuille flow.
Physics of Fluids,
Vol. 36,
Issue. 4,
Oxley, William
and
Kerswell, Rich R.
2024.
Linear stability of stratified, rotating, viscous plane Couette–Poiseuille flow.
Journal of Fluid Mechanics,
Vol. 991,
Issue. ,
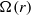 $\Omega (r)$ increases along the radial direction, a regime never explored before. The instability is highly non-axisymmetric and involves the resonance of two families of inertia–gravity waves like for the strato-rotational instability. The growth rate is maximum when only the outer cylinder is rotating and goes to zero when
$\Omega (r)$ increases along the radial direction, a regime never explored before. The instability is highly non-axisymmetric and involves the resonance of two families of inertia–gravity waves like for the strato-rotational instability. The growth rate is maximum when only the outer cylinder is rotating and goes to zero when 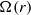 $\Omega (r)$ is constant. The sufficient condition for linear, inviscid instability derived previously,
$\Omega (r)$ is constant. The sufficient condition for linear, inviscid instability derived previously, 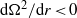 $\mathrm{d} {\Omega }^{2} / \mathrm{d} r\lt 0$, is therefore extended to
$\mathrm{d} {\Omega }^{2} / \mathrm{d} r\lt 0$, is therefore extended to 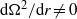 $\mathrm{d} {\Omega }^{2} / \mathrm{d} r\not = 0$, meaning that only the regime of solid-body rotation is stable in stratified fluids. A Wentzel–Kramers–Brillouin–Jeffreys (WKBJ) analysis in the inviscid limit, confirmed by the numerical results, shows that the instability occurs only when the Froude number is below a critical value and only for a particular band of azimuthal wavenumbers. It is also demonstrated that the instability originates from a reversal of the radial group velocity of the waves, or equivalently from a wave over-reflection phenomenon. The instability persists in the presence of viscous effects.
$\mathrm{d} {\Omega }^{2} / \mathrm{d} r\not = 0$, meaning that only the regime of solid-body rotation is stable in stratified fluids. A Wentzel–Kramers–Brillouin–Jeffreys (WKBJ) analysis in the inviscid limit, confirmed by the numerical results, shows that the instability occurs only when the Froude number is below a critical value and only for a particular band of azimuthal wavenumbers. It is also demonstrated that the instability originates from a reversal of the radial group velocity of the waves, or equivalently from a wave over-reflection phenomenon. The instability persists in the presence of viscous effects.