Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-10T06:11:16.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of two-dimensional collapsible-channel flow at high Reynolds number

Published online by Cambridge University Press:  16 February 2012

Ramesh B. Kudenatti ,
N. M. Bujurke  and
T. J. Pedley
Ramesh B. Kudenatti
Affiliation:
Department of Mathematics, Bangalore University, Bangalore-560 001, India Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
N. M. Bujurke
Affiliation:
Department of Mathematics, Karnatak University, Dharwad-580 003, India
T. J. Pedley*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the linear stability of two-dimensional high-Reynolds-number flow in a rigid parallel-sided channel, of which part of one wall has been replaced by a flexible membrane under longitudinal tension 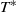. Far upstream the flow is parallel Poiseuille flow at Reynolds number 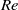; the width of the channel is and the length of the membrane is 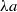, where 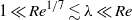. Steady flow was studied using interactive boundary-layer theory by Guneratne & Pedley (J. Fluid Mech., vol. 569, 2006, pp. 151–184) for various values of the pressure difference 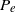across the membrane at its upstream end. Here unsteady interactive boundary-layer theory is used to investigate the stability of the trivial steady solution for 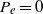. An unexpected finding is that the flow is always unstable, with a growth rate that increases with 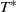. In other words, the stability problem is ill-posed. However, when the pressure difference is held fixed (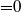) at the downstream end of the membrane, or a little further downstream, the problem is well-posed and all solutions are stable. The physical mechanisms underlying these findings are explored using a simple inviscid model; the crucial factor in the fluid dynamics is the vorticity gradient across the incoming Poiseuille flow.

JFM classification

Instability: Instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 705: Special issue dedicated to Professor T. J. Pedley on his 70th birthday , 25 August 2012 , pp. 371 - 386
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Abramowitz, M. & Stegun, I. A. 1970 Handbook of Mathematical Functions. Dover.Google Scholar
2. Bertram, C. D., Raymond, C. J. & Pedley, T. J. 1991 Application of nonlinear dynamics concepts to the analysis of self-excited oscillations of a collapsible tube conveying flow. J. Fluids Struct. 5, 391–426.CrossRefGoogle Scholar
3. Bogdanova, E. V. & Ryzhov, O. S. 1983 Free and induced oscillations in Poiseuille flow. Q. J. Mech. Appl. Maths 36, 271–287.CrossRefGoogle Scholar
4. Conrad, W. A. 1969 Pressure flow relationships in collapsible tubes. IEEE Trans. Bio-Med. Engng 16, 284–295.CrossRefGoogle ScholarPubMed
5. Fabijonas, B. R., Lozier, D. W. & Olver, F. W. J. 2004 Computation of complex Airy functions and their zeros using asymptotics and the differential equations. ACM Trans. Math. Softw. 30, 471–490.CrossRefGoogle Scholar
6. Gil, A., Segura, J. & Temme, N. M. 2002 Algorithm 822: GIZ, HIZ: Two Fortran 77 routines for the computation of complex Scorer functions. ACM Trans. Math. Softw. 28, 436–447.CrossRefGoogle Scholar
7. Guneratne, J. C. & Pedley, T. J. 2006 High-Reynolds-number steady flow in a collapsible channel. J. Fluid Mech. 569, 151–184.CrossRefGoogle Scholar
8. Jensen, O. E. 1990 Instabilities of flow in a collapsed tube. J. Fluid Mech. 220, 623–659.CrossRefGoogle Scholar
9. Jensen, O. E. & Heil, M. 2003 High-frequency self-excited oscillations in a collapsible-channel flow. J. Fluid Mech. 481, 235–268.CrossRefGoogle Scholar
10. Katz, A. I., Chen, Y. & Moreno, A. H. 1969 Flow through a collapsible tube. Biophys. J. 9, 1261–1279.CrossRefGoogle ScholarPubMed
11. Luo, X. Y., Cai, Z. X., Li, W. G. & Pedley, T. J. 2008 The cascade structure of linear instability in collapsible channel flow. J. Fluid Mech. 600, 45–76.CrossRefGoogle Scholar
12. Luo, X. Y. & Pedley, T. J. 1996 A numerical simulation of unsteady flows in a two-dimensional collapsible channel. J. Fluid Mech. 314, 191–225.CrossRefGoogle Scholar
13. Luo, X. Y. & Pedley, T. J. 1998 The effects of wall inertia on flow in a two-dimensional collapsible channel. J. Fluid Mech. 363, 253–280.CrossRefGoogle Scholar
14. Pedley, T. J. 1980 The Fluid Mechanics of Large Blood Vessels. Cambridge University Press.CrossRefGoogle Scholar
15. Pedley, T. J. 2000 Blood flow in arteries and veins. In Perspectives in Fluid Dynamics (ed. Batchelor, G. K., Moffatt, H. K. & Worster, M. G. ), pp. 105–158. Cambridge University Press.Google Scholar
16. Pedley, T. J. & Stephanoff, K. D. 1985 Flow along a channel with a time-dependent indentation in one wall. J. Fluid Mech. 160, 337–367.CrossRefGoogle Scholar
17. Pihler-Puzovic, D. 2011 PhD thesis, University of Cambridge, Cambridge.Google Scholar
18. Shapiro, A. H. 1977 Steady flow in collapsible tubes. Trans ASME: J. Biomech. Engng 99, 126–147.Google Scholar
19. Smith, F. T. 1976a Flow through constricted or dilated pipes and channels. Part I. Q. J. Mech. Appl. Maths 29, 343–364.CrossRefGoogle Scholar
20. Smith, F. T. 1976b Flow through constricted or dilated pipes and channels. Part II. Q. J. Mech. Appl. Maths 29, 365–376.CrossRefGoogle Scholar
21. Stewart, P. S., Heil, M., Waters, S. L. & Jensen, O. E. 2010 Sloshing and slamming oscillations in collapsible channel flow. J. Fluid Mech. 662, 288–319.CrossRefGoogle Scholar
22. Stewart, P. S., Waters, S. L. & Jensen, O. E. 2009 Local and global instabilities of flow in a flexible-walled channel. Eur. J. Mech. B 28, 541–557.CrossRefGoogle Scholar