Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-25T16:36:45.591Z Has data issue: false hasContentIssue false
  • English
  • Français

Stability of Taylor–Couette flow with oscillatory radial throughflow

Published online by Cambridge University Press:  19 December 2024

Cheng-Cheng Wang ,
Peng Gao Open the ORCID record for Peng Gao [Opens in a new window]  and
Xi-Yun Lu Open the ORCID record for Xi-Yun Lu [Opens in a new window]
Cheng-Cheng Wang
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Peng Gao*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Xi-Yun Lu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

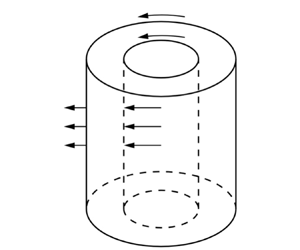
The stability of Taylor–Couette flow modulated by oscillatory wall suction/blowing is investigated using Floquet linear stability analysis. The growth rate and stability mode are obtained by numerical calculation and asymptotic expansion. By calculating the effect of wall suction/blowing on the critical mode of steady Taylor–Couette flow, it is found that for most suction/blowing parameters, the maximum disturbance growth rate of the critical mode decreases and the flow becomes more stable. Only in a very small parameter region, wall suction/blowing increases the maximum disturbance growth rate of the critical mode, resulting in flow instability when the gap between the cylinders is large. The asymptotic results for small suction/blowing amplitudes indicate that the change of flow instability is mainly due to the steady correction of the basic flow induced by the modulation. A parametric study of the critical inner Reynolds number and the associated critical wavenumber is performed. It is found that the flow is stabilized by the modulation for most of the parameter ranges considered. For a wide gap between the cylinders, it is possible for the system to be mildly destabilized by weak suction/blowing.

JFM classification

Flow Control: Instability control Instability: Shear-flow instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 1001 , 25 December 2024 , A57
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andereck, C.D., Liu, S.S. & Swinney, H.L. 1986 Flow regimes in a circular Couette system with independently rotating cylinders. J. Fluid Mech. 164, 155–183.CrossRefGoogle Scholar
Avila, M., Belisle, M.J., Lopez, J.M., Marques, F. & Saric, W.S. 2008 Mode competition in modulated Taylor–Couette flow. J. Fluid Mech. 601, 381–406.CrossRefGoogle Scholar
Bahl, S.K. 1970 Stability of viscous flow between two concentric rotating porous cylinders. Def. Sci. J. 20, 89–96.Google Scholar
Bewley, T.R. & Liu, S. 1998 Optimal and robust control and estimation of linear paths to transition. J. Fluid Mech. 365, 305–349.CrossRefGoogle Scholar
Bewley, T.R., Moin, P. & Temam, R. 2001 DNS-based predictive control of turbulence: an optimal benchmark for feedback algorithms. J. Fluid Mech. 447, 179–225.CrossRefGoogle Scholar
Chang, T.S. & Sartory, W.K. 1967 Hydromagnetic stability of dissipative flow between rotating permeable cylinders. J. Fluid Mech. 27 (1), 65–79.CrossRefGoogle Scholar
Chang, T.S. & Sartory, W.K. 1969 Hydromagnetic stability of dissipative flow between rotating permeable cylinders. Part 2. Oscillatory critical modes and asymptotic results. J. Fluid Mech. 36 (1), 193–206.CrossRefGoogle Scholar
Chung, K.C. & Astill, K.N. 1977 Hydrodynamic instability of viscous flow between rotating coaxial cylinders with fully developed axial flow. J. Fluid Mech. 81 (4), 641–655.CrossRefGoogle Scholar
Coles, D. 1965 Transition in circular Couette flow. J. Fluid Mech. 21 (3), 385–425.CrossRefGoogle Scholar
Cotrell, D.L. & Pearlstein, A.J. 2004 The connection between centrifugal instability and Tollmien–Schlichting-like instability for spiral Poiseuille flow. J. Fluid Mech. 509, 331–351.CrossRefGoogle Scholar
Davis, S.H. 1976 The stability of time-periodic flows. Annu. Rev. Fluid Mech. 8, 57–74.CrossRefGoogle Scholar
Donnelly, R.J. & Schwarz, K.W. 1965 Experiments on the stability of viscous flow between rotating cylinders-VI. Finite-amplitude experiments. Proc. R. Soc. Lond. A 283 (1395), 531–556.Google Scholar
Dubrulle, B., Dauchot, O., Daviaud, F., Longaretti, P.-Y., Richard, D. & Zahn, J.-P. 2005 Stability and turbulent transport in Taylor–Couette flow from analysis of experimental data. Phys. Fluids 17 (9), 095103.CrossRefGoogle Scholar
Floryan, J.M. 1997 Stability of wall-bounded shear layers in the presence of simulated distributed surface roughness. J. Fluid Mech. 335, 29–55.CrossRefGoogle Scholar
Fuentes, F., Goluskin, D. & Chernyshenko, S. 2022 Global stability of fluid flows despite transient growth of energy. Phys. Rev. Lett. 128, 204502.CrossRefGoogle ScholarPubMed
Gallet, B., Doering, C.R. & Spiegel, E.A. 2010 Destabilizing Taylor–Couette flow with suction. Phys. Fluids 22 (3), 034105.CrossRefGoogle Scholar
Gao, P. & Lu, X.Y. 2006 a Effects of wall suction/injection on the linear stability of flat Stokes layers. J. Fluid Mech. 551, 303–308.CrossRefGoogle Scholar
Gao, P. & Lu, X.Y. 2006 b Instability of channel flow with oscillatory wall suction/blowing. Phys. Fluids 18 (3), 034102.CrossRefGoogle Scholar
Heise, M., Hoffmann, C., Abshagen, J., Pinter, A., Pfister, G. & Lücke, M. 2008 Stabilization of domain walls between traveling waves by nonlinear mode coupling in Taylor–Couette flow. Phys. Rev. Lett. 100 (6), 064501.CrossRefGoogle ScholarPubMed
Heise, M., Hoffmann, C., Will, C., Altmeyer, S., Abshagen, J. & Pfister, G. 2013 Co-rotating Taylor–Couette flow enclosed by stationary disks. J. Fluid Mech. 716, R4.CrossRefGoogle Scholar
Hoffmann, C., Altmeyer, S., Heise, M., Abshagen, J. & Pfister, G. 2013 Axisymmetric propagating vortices in centrifugally stable Taylor–Couette flow. J. Fluid Mech. 728, 458–470.CrossRefGoogle Scholar
Hristova, H., Roch, S., Schmid, P.J. & Tuckerman, L.S. 2002 Transient growth in Taylor–Couette flow. Phys. Fluids 14 (10), 3475–3484.CrossRefGoogle Scholar
Ilin, K. & Morgulis, A. 2013 Instability of an inviscid flow between porous cylinders with radial flow. J. Fluid Mech. 730, 364–378.CrossRefGoogle Scholar
Ilin, K. & Morgulis, A. 2017 Inviscid instability of an incompressible flow between rotating porous cylinders to three-dimensional perturbations. Eur. J. Mech. (B/Fluids) 61, 46–60.CrossRefGoogle Scholar
Johnson, E.C. & Lueptow, R.M. 1997 Hydrodynamic stability of flow between rotating porous cylinders with radial and axial flow. Phys. Fluids 9 (12), 3687–3696.CrossRefGoogle Scholar
Joshi, S.S., Speyer, J.L. & Kim, J. 1997 A systems theory approach to the feedback stabilization of infinitesimal and finite-amplitude disturbances in plane Poiseuille flow. J. Fluid Mech. 332, 157–184.CrossRefGoogle Scholar
Joslin, R.D. 1998 Aircraft laminar flow control. Annu. Rev. Fluid Mech. 30 (1), 1–29.CrossRefGoogle Scholar
Khapko, T., Schlatter, P., Duguet, Y. & Henningson, D.S. 2016 Turbulence collapse in a suction boundary layer. J. Fluid Mech. 795, 356–379.CrossRefGoogle Scholar
Kolyshkin, A.A. & Vaillancourt, R 1997 Convective instability boundary of Couette flow between rotating porous cylinders with axial and radial flows. Phys. Fluids 9 (4), 910–918.CrossRefGoogle Scholar
Krueger, E.R., Gross, A. & Diprima, R.C. 1966 On the relative importance of Taylor–vortex and non-axisymmetric modes in flow between rotating cylinders. J. Fluid Mech. 24 (3), 521–538.CrossRefGoogle Scholar
Langford, W.F., Tagg, R., Kostelich, E., Swinney, H. & Golubitsky, M. 1988 Primary instabilities and bicriticality in flow between counter-rotating cylinders. Phys. Fluids 31 (4), 776.CrossRefGoogle Scholar
Lee, S. & Lueptow, R.M. 2004 Rotating reverse osmosis for water recovery in space: influence of operational parameters on RO performance. Desalination 169 (2), 109–120.CrossRefGoogle Scholar
Lee, S. & Lueptow, R.M. 2005 Model predictions and experiments for rotating reverse osmosis for space mission water reuse. Sep. Sci. Technol. 39 (3), 539–561.CrossRefGoogle Scholar
Lueptow, R.M. & Hajiloo, A. 1995 Flow in a rotating membrane plasma separator. ASAIO J. 41 (2), 182–188.CrossRefGoogle Scholar
Maretzke, S., Hof, B. & Avila, M. 2014 Transient growth in linearly stable Taylor–Couette flows. J. Fluid Mech. 742, 254–290.CrossRefGoogle Scholar
Marques, F. & Lopez, J.M. 1997 Taylor–Couette flow with axial oscillations of the inner cylinder: Floquet analysis of the basic flow. J. Fluid Mech. 348, 153–175.CrossRefGoogle Scholar
Martinand, D., Serre, E. & Lueptow, R.M. 2009 Absolute and convective instability of cylindrical Couette flow with axial and radial flows. Phys. Fluids 21 (10), 104102.CrossRefGoogle Scholar
Martinand, D., Serre, E. & Lueptow, R.M. 2017 Linear and weakly nonlinear analyses of cylindrical Couette flow with axial and radial flows. J. Fluid Mech. 824, 438–476.CrossRefGoogle Scholar
Messing, R. & Kloker, M.J. 2010 Investigation of suction for laminar flow control of three-dimensional boundary layers. J. Fluid Mech. 658, 117–147.CrossRefGoogle Scholar
Min, K. & Lueptow, R.M. 1994 Hydrodynamic stability of viscous flow between rotating porous cylinders with radial flow. Phys. Fluids 6 (1), 144–151.CrossRefGoogle Scholar
Mochalin, I., Cai, J., Shiju, E., Brazhenko, V. & Wang, D. 2022 Numerical study of the flow through an annular gap with filtration by a rotating porous cylinder. Engng Appl. Comput. Fluid Mech. 16 (1), 469–483.Google Scholar
Morón, D., Feldmann, D. & Avila, M. 2022 Effect of waveform on turbulence transition in pulsatile pipe flow. J. Fluid Mech. 948, A20.CrossRefGoogle Scholar
Or, A.C. 1997 Finite-wavelength instability in a horizontal liquid layer on an oscillating plane. J. Fluid Mech. 335, 213–232.CrossRefGoogle Scholar
Pearlstein, A.J. 1981 Effect of rotation on the stability of a doubly diffusive fluid layer. J. Fluid Mech. 103, 389–412.CrossRefGoogle Scholar
Schmid, P.J. & Henningson, D.S. 2001 Eigensolutions to the viscous problem. In Stability and Transition in Shear Flows (ed. J.E. Marsden & L. Sirovich), pp. 55–98. Applied Mathematical Sciences, vol. 142. Springer.CrossRefGoogle Scholar
Schwille, J.A., Mitra, D. & Lueptow, R.M. 2002 Design parameters for rotating cylindrical filtration. J. Membr. Sci. 204 (1-2), 53–65.CrossRefGoogle ScholarPubMed
Van Gils, D.P., Huisman, S.G., Bruggert, G.W., Sun, C. & Lohse, D. 2011 Torque scaling in turbulent Taylor–Couette flow with co-and counterrotating cylinders. Phys. Rev. Lett. 106 (2), 024502.CrossRefGoogle ScholarPubMed
Wang, B., Ayats, R., Deguchi, K., Mellibovsky, F. & Meseguer, A. 2022 Self-sustainment of coherent structures in counter-rotating Taylor–Couette flow. J. Fluid Mech. 951, A21.CrossRefGoogle Scholar
Weisberg, A.Y., Kevrekidis, I.G. & Smits, A.J. 1997 Delaying transition in Taylor–Couette flow with axial motion of the inner cylinder. J. Fluid Mech. 348, 141–151.CrossRefGoogle Scholar
Xu, D., Varshney, A., Ma, X., Song, B., Riedl, M., Avila, M. & Hof, B. 2020 Nonlinear hydrodynamic instability and turbulence in pulsatile flow. Proc. Natl Acad. Sci. USA 117 (21), 11233–11239.CrossRefGoogle ScholarPubMed
Zheng, J., Cai, J., Wang, D. & Mochalin, I. 2019 Suspended particle motion close to the surface of rotating cylindrical filtering membrane. Phys. Fluids 31 (5), 053302.CrossRefGoogle Scholar