Published online by Cambridge University Press: 23 November 2015
We investigate mechanisms through which energy cascades from the mesoscale, 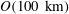 $O(100~\text{km})$, to the submesoscale,
$O(100~\text{km})$, to the submesoscale, 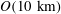 $O(10~\text{km})$, for oceanic fronts in a reduced gravity shallow water model using two different profiles. The first idealization of an ocean front has an interfacial depth that is a smooth hyperbolic tangent profile and is an extension of the piecewise constant potential vorticity profile studied in Boss et al. (J. Fluid Mech., vol. 315, 1996, pp. 65–84). By considering a range of minimum depths, all of which have the same velocity profile, we are better able to isolate the effect of vanishing layer depths. We find that the most unstable mode exists in a one-layer model and does not need two layers, as previously speculated. Moreover, we find that even without a vanishing layer depth there are other modes that appear at both larger and smaller length scales that have a gravity wave structure. The second profile is the parabolic double front from Scherer & Zeitlin (J. Fluid Mech., vol. 613, 2008, pp. 309–327). We find more unstable modes than previously presented and also categorize them based on the mode number. In particular, we find there are pairs of unstable modes that have equal growth rates. We also study the nonlinear evolution of these oceanic fronts. It is determined that vanishing layer depths have significant effects on the unstable dynamics that arise. First, stronger gravity wave fields are generated. Second, cyclonic fluid that moves into the deeper waters is stretched preferentially more in comparison to the deep water scenario and destabilizes more easily. This results in smaller scale vortices, both cyclones and anticyclones, that have length scales in the submesoscale regime. Our results suggest that the nonlinear dynamics of a front can be very efficient at generating submesoscale motions.
$O(10~\text{km})$, for oceanic fronts in a reduced gravity shallow water model using two different profiles. The first idealization of an ocean front has an interfacial depth that is a smooth hyperbolic tangent profile and is an extension of the piecewise constant potential vorticity profile studied in Boss et al. (J. Fluid Mech., vol. 315, 1996, pp. 65–84). By considering a range of minimum depths, all of which have the same velocity profile, we are better able to isolate the effect of vanishing layer depths. We find that the most unstable mode exists in a one-layer model and does not need two layers, as previously speculated. Moreover, we find that even without a vanishing layer depth there are other modes that appear at both larger and smaller length scales that have a gravity wave structure. The second profile is the parabolic double front from Scherer & Zeitlin (J. Fluid Mech., vol. 613, 2008, pp. 309–327). We find more unstable modes than previously presented and also categorize them based on the mode number. In particular, we find there are pairs of unstable modes that have equal growth rates. We also study the nonlinear evolution of these oceanic fronts. It is determined that vanishing layer depths have significant effects on the unstable dynamics that arise. First, stronger gravity wave fields are generated. Second, cyclonic fluid that moves into the deeper waters is stretched preferentially more in comparison to the deep water scenario and destabilizes more easily. This results in smaller scale vortices, both cyclones and anticyclones, that have length scales in the submesoscale regime. Our results suggest that the nonlinear dynamics of a front can be very efficient at generating submesoscale motions.
Animation of the divergence of the mass flux for the nonlinear simulation of the parabolic double front.
Animation of the layer depth for the nonlinear simulation of the parabolic double front.
Animation of the vorticity for the nonlinear simulation of the parabolic double front.
Animation of the divergence of the mass flux for the nonlinear simulation of the Bickley jet with d = 0.
Animation of the layer depth for the nonlinear simulation of the Bickley jet with d = 0.
Animation of the vorticity for the nonlinear simulation of the Bickley jet with d = 0
Animation of the divergence of the mass flux for the nonlinear simulation of the Bickley jet with d = 150.