Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T04:04:15.689Z Has data issue: false hasContentIssue false
  • English
  • Français

Spontaneous radiation of sound by instability of a highly cooled hypersonic boundary layer

Published online by Cambridge University Press:  16 September 2016

Pavel V. Chuvakhov Open the ORCID record for Pavel V. Chuvakhov [Opens in a new window]  and
Alexander V. Fedorov
Pavel V. Chuvakhov*
Affiliation:
Central Aerodynamic Institute, 1 Zhukovskogo Str., Zhukovsky, Moscow reg., 140180, Russian Federation Moscow Institute of Physics and Technology, 9 Institutsky per., Dolgoprudny, Moscow reg., 141700, Russian Federation
Alexander V. Fedorov
Affiliation:
Moscow Institute of Physics and Technology, 9 Institutsky per., Dolgoprudny, Moscow reg., 141700, Russian Federation
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The linear stability analysis predicts that the Mack second mode propagating in the boundary layer on a sufficiently cold plate can radiate acoustic waves into the outer inviscid flow. This effect, which is called as a spontaneous radiation (or emission) of sound, is associated with synchronization of the second mode with slow acoustic waves of the continuous spectrum. 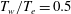The theoretical predictions are confirmed by direct numerical simulations of wave trains and wave packets propagating in the boundary layer on a flat plate at free-stream Mach number 6 and wall-to-edge temperature ratio $T_{w}/T_{e}=0.5$. A non-uniform distribution of the wave packet components and the interference between the radiated acoustic waves result in an intricate pattern of the outer acoustic field. The spontaneous radiation of sound, in turn, strongly affects the wave packet in the boundary layer causing its elongation and modulation. This phenomenon may alter the downstream development of instability and delay the transition onset.

JFM classification

Boundary Layers: Boundary layer stability Boundary Layers: Boundary Layers Aerodynamics: High-speed flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 805 , 25 October 2016 , pp. 188 - 206
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balakumar, P. & Malik, M. R. 1992 Discrete modes and continuous spectra in supersonic boundary layers. J. Fluid Mech. 239, 631–656.CrossRefGoogle Scholar
Bitter, N. P. & Shepherd, J. E. 2015 Stability of highly cooled hypervelocity boundary layers. J. Fluid Mech. 778, 586–620.CrossRefGoogle Scholar
Brès, G. A., Inkman, M., Colonius, T. & Fedorov, A. V. 2013 Second-mode attenuation and cancellation by porous coatings in a high-speed boundary layer. J. Fluid Mech. 726, 312–337.CrossRefGoogle Scholar
Chang, C.-L., Malik, M. & Hussaini, M. 1990 Effects of shock on the stability of hypersonic boundary layers. In 21st Fluid Dynamics, Plasma Dynamics and Lasers Conference, American Institute of Aeronautics and Astronautics; AIAA Paper 90-1448.Google Scholar
Chang, C.-L., Vinh, H. & Malik, M. 1997 Hypersonic boundary-layer stability with chemical reactions using PSE. In 28th Fluid Dynamics Conference, American Institute of Aeronautics and Astronautics; AIAA Paper 97-2012.Google Scholar
Egorov, I. V., Fedorov, A. V. & Soudakov, V. G. 2006 Direct numerical simulation of disturbances generated by periodic suction-blowing in a hypersonic boundary layer. Theor. Comput. Fluid Dyn. 20 (1), 41–54.CrossRefGoogle Scholar
Egorov, I. V., Fedorov, A. V. & Soudakov, V. G. 2008 Receptivity of a hypersonic boundary layer over a flat plate with a porous coating. J. Fluid Mech. 601, 165–187.CrossRefGoogle Scholar
Fedorov, A., Brès, G., Inkman, M. & Colonius, T. 2011 Instability of hypersonic boundary layer on a wall with resonating micro-cavities. In 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, American Institute of Aeronautics and Astronautics; AIAA Paper 2011-373.Google Scholar
Fedorov, A. & Tumin, A. 2003 Initial-value problem for hypersonic boundary-layer flows. AIAA J. 41 (3), 379–389.CrossRefGoogle Scholar
Fedorov, A. V. 2011 Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 43, 79–95.CrossRefGoogle Scholar
Fedorov, A. V. 2013 Receptivity of a supersonic boundary layer to solid particulates. J. Fluid Mech. 737, 105–131.CrossRefGoogle Scholar
Fedorov, A. V. & Khokhlov, A. P. 2001 Prehistory of instability in a hypersonic boundary layer. Theor. Comput. Fluid Dyn. 14 (6), 359–375.CrossRefGoogle Scholar
Fedorov, A. V., Ryzhov, A. A., Soudakov, V. G. & Utyuzhnikov, S. V. 2013 Receptivity of a high-speed boundary layer to temperature spottiness. J. Fluid Mech. 722, 533–553.CrossRefGoogle Scholar
Fedorov, A. V., Soudakov, V. & Leyva, I. A. 2014 Stability analysis of high-speed boundary-layer flow with gas injection. In 7th AIAA Theoretical Fluid Mechanics Conference, American Institute of Aeronautics and Astronautics; AIAA Paper 2014-2498.Google Scholar
Jiang, G.-S. & Shu, C.-W. 1996 Efficient implementation of weighted ENO schemes. J. Comput. Phys. 126 (1), 202–228.CrossRefGoogle Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid Mechanics, 2nd edn. Course of Theoretical Physics, vol. 6. Pergamon; second English Edition, Revised.Google Scholar
Mack, L. M. 1987 Review of linear compressible stability theory. In Stability of Time Dependent and Spatially Varying Flows, pp. 164–187. Springer.CrossRefGoogle Scholar
Morkovin, M. V., Reshotko, E. & Herbert, Th. 1994 Transition in open flow systems: a reassessment. Bull. Am. Phys. Soc. 39 (9), 1–31.Google Scholar
Nakamura, T. & Sherman, M. M. 1970 Flight test measurements of boundary-layer transition on a nonablating 22 deg cone. J. Spacecr. Rockets 7 (2), 137–142.Google Scholar
Nayfeh, A. H. 1980 Stability of three-dimensional boundary layers. AIAA J. 18 (4), 406–416.CrossRefGoogle Scholar
Tumin, A. M. & Fedorov, A. V. 1983 Spatial growth of disturbances in a compressible boundary layer. J. Appl. Mech. Tech. Phys. 24 (4), 548–554.CrossRefGoogle Scholar
Wright, R. & Zoby, E. 1977 Flight boundary layer transition measurements on a slender cone at mach 20. In 10th Fluid and Plasmadynamics Conference, American Institute of Aeronautics and Astronautics; AIAA Paper 77-719.Google Scholar

Chuvakhov Supplementary Material

Movie 1. Wave packet dynamics on the nearly-adiabatic wall, Tw/Te=7: pressure disturbance field (top) and wall pressure disturbance distribution (bottom)

Download Chuvakhov Supplementary Material(Video)
Video 285.5 KB

Chuvakhov Supplementary Material

Movie 2. LF wave packet dynamics, Tw/Te=0.5: pressure disturbance field (top) and wall pressure disturbance distribution (bottom)

Download Chuvakhov Supplementary Material(Video)
Video 717.9 KB