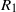We conduct a series of laboratory experiments to study the mixing of an initially linear stratification in turbulent Taylor–Couette flow. We vary the inner radius, ${R}_{1} $, and rotation rate, 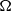$\Omega $, relative to the fixed outer cylinder, of radius 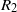${R}_{2} $, as well as the initial buoyancy frequency 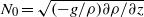${N}_{0} = \sqrt{(- g/ \rho )\partial \rho / \partial z} $. We find that a linear stratification spontaneously splits into a series of layers and interfaces. The characteristic height of these layers is proportional to 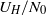${U}_{H} / {N}_{0} $, where 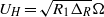${U}_{H} = \sqrt{{R}_{1} { \mathrm{\Delta} }_{R} } \Omega $ is a horizontal velocity scale, with 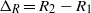${ \mathrm{\Delta} }_{R} = {R}_{2} - {R}_{1} $ the gap width of the annulus. The buoyancy flux through these layers matches the equivalent flux through a two-layer stratification, independently of the height or number of layers. For a strongly stratified flow, the flux tends to an asymptotic constant value, even when multiple layers are present, consistent with Woods et al. (J. Fluid Mech., vol. 663, 2010, pp. 347–357). For smaller stratification the flux increases, reaching a maximum just before the layers disappear due to overturning of the interfaces.