Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T04:37:58.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Spin-up of a two-component superfluid: analytic theory in arbitrary geometry

Published online by Cambridge University Press:  18 July 2013

Cornelis A. van Eysden  and
A. Melatos
Cornelis A. van Eysden*
Affiliation:
School of Physics, University of Melbourne, Parkville, VIC 3010, Australia
A. Melatos
Affiliation:
School of Physics, University of Melbourne, Parkville, VIC 3010, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The impulsive spin-up of a two-component superfluid and its container is solved analytically for the first time in arbitrary geometry, generalizing the extensively studied case of single-fluid spin-up. The superfluid is modelled by the Hall–Vinen–Bekarevich–Khalatnikov (HVBK) two-fluid equations, neglecting non-hydrodynamic processes like vortex tension and pinning, which are weak in certain applications (e.g. neutron stars) and confined to boundary layers in the inviscid HVBK component in other applications (e.g. helium II spin-up in smooth-walled containers). Both components of the flow are found to be columnar. The spin-up time depends on the geometry, mutual friction coefficients, $B$, 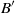${B}^{\prime } $, the Ekman number 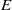$E$, and the superfluid density fraction 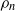${\rho }_{n} $. For 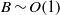$B\sim O(1)$, the inviscid component undergoes Ekman pumping due to strong coupling to the viscous component, and the azimuthal velocities are ‘locked together’ during the spin-up. For 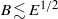$B\lesssim {E}^{1/ 2} $, there is no Ekman pumping in the inviscid component and the inviscid azimuthal velocity spins up via mutual friction on a combination of the mutual friction and Ekman time scales. The spin-up process is studied in spheres, cylinders (with co- and counter-rotating lids), and cones, and occurs faster in spheres and cones. Ekman pumping is (anti-) clockwise adjacent to the (lower-) upper-right boundary, and mirrored about the rotation axis. The solution obtained by Reisenegger (J. Low Temp. Phys., vol. 92, 1993, p. 77) between slowly accelerating parallel plates is recovered in the associated limit. The hydrodynamic torque on the container decays dual-exponentially with time in a cylinder but not in a sphere or cone, where it is a superposition of exponentials whose time scales vary with latitude. The torque is a good diagnostic of the flow; e.g. it is steepest initially in a sphere with strong mutual friction.

JFM classification

Complex Fluids: Complex Fluids Complex Fluids: Quantum fluids
Type
Papers
Information
Journal of Fluid Mechanics , Volume 729 , 25 August 2013 , pp. 180 - 213
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abney, M. & Epstein, R. I. 1996 Ekman pumping in compact astrophysical bodies. J. Fluid Mech. 312, 327–340.CrossRefGoogle Scholar
Adams, P. W., Cieplak, M. & Glaberson, W. I. 1985 Spin-up problem in superfluid 4He. Phys. Rev. B 32, 171–177.CrossRefGoogle ScholarPubMed
Amberg, G. & Ungarish, M. 1993 Spin-up from rest of a mixture: numerical simulation and asymptotic theory. J. Fluid Mech. 246, 443–464.CrossRefGoogle Scholar
Anderson, P. W. & Itoh, N. 1975 Pulsar glitches and restlessness as a hard superfluidity phenomenon. Nature 256, 25–27.CrossRefGoogle Scholar
Anderson, P. W., Pines, D., Ruderman, M. & Shaham, J. 1978 Questions about rotating superfluid dynamics: problems of pulsar astrophysics accessible in the laboratory. J. Low Temp. Phys. 30, 839–847.CrossRefGoogle Scholar
Andersson, N., Sidery, T. & Comer, G. L. 2006 Mutual friction in superfluid neutron stars. Mon. Not. R. Astron. Soc. 368, 162–170.CrossRefGoogle Scholar
Barenghi, C. F. 1992 Vortices and the Couette flow of helium II. Phys. Rev. B 45, 2290–2293.CrossRefGoogle ScholarPubMed
Barenghi, C. F., Donnelly, R. J. & Vinen, W. F. 1983 Friction on quantized vortices in helium II. A review. J. Low Temp. Phys. 52, 189–247.CrossRefGoogle Scholar
Barenghi, C. F. & Jones, C. A. 1988 The stability of the Couette flow of helium II. J. Fluid Mech. 197, 551–569.CrossRefGoogle Scholar
Baym, G. & Chandler, E. 1983 The hydrodynamics of rotating superfluids. Part 1. Zero-temperature, nondissipative theory. J. Low Temp. Phys. 50, 57–87.Google Scholar
Baym, G., Epstein, R. I. & Link, B. 1992 Dynamics of vortices in neutron stars. Phys. B Condens. Matter 178, 1–12.CrossRefGoogle Scholar
Baym, G., Pethick, C. & Pines, D. 1969 Superfluidity in neutron stars. Nature 224, 673–674.CrossRefGoogle Scholar
Benton, E. R. & Clark, A. 1974 Spin-up. Annu. Rev. Fluid Mech. 6, 257–280.CrossRefGoogle Scholar
Benton, E. R. & Loper, D. E. 1969 On the spin-up of an electrically conducting fluid. Part 1. The unsteady hydromagnetic Ekman–Hartmann boundary-layer problem. J. Fluid Mech. 39, 561–586.CrossRefGoogle Scholar
Bondi, H. & Lyttleton, R. A. 1948 On the dynamical theory of the rotation of the earth. Proc. Camb. Phil. Soc. 44, 345–359.CrossRefGoogle Scholar
Campbell, L. J. & Krasnov, Y. K. 1982 Transient behavior of rotating superfluid helium. J. Low Temp. Phys. 49, 377–396.CrossRefGoogle Scholar
Chandler, E. & Baym, G. 1986 The hydrodynamics of rotating superfluids. Part 2. Finite temperature, dissipative theory. J. Low Temp. Phys. 62, 119–142.Google Scholar
Cutler, C. & Lindblom, L. 1987 The effect of viscosity on neutron star oscillations. Astrophys. J. 314, 234–241.CrossRefGoogle Scholar
Donnelly, R. J. 2005 Quantized Vortices in Helium II. Cambridge University Press.Google Scholar
Donnelly, R. J. 2012 URL: http://darkwing.uoregon.edu/~rjd/vapor1.htm.Google Scholar
Drew, D. A. & Passman, S. L. 1999 Theory of Multicomponent Fluids. Springer.CrossRefGoogle Scholar
Easson, I. 1979 Postglitch behavior of the plasma inside neutron stars. Astrophys. J. 228, 257–267.CrossRefGoogle Scholar
Eltsov, V. B., de Graaf, R., Heikkinen, P. J., Hosio, J. J., Hänninen, R., Krusius, M. & L’Vov, V. S. 2010 Stability and dissipation of laminar vortex flow in superfluid 3He-B. Phys. Rev. Lett. 105 (12), 125301.CrossRefGoogle ScholarPubMed
Finne, A. P., Araki, T., Blaauwgeers, R., Eltsov, V. B., Kopnin, N. B., Krusius, M., Skrbek, L., Tsubota, M. & Volovik, G. E. 2003 An intrinsic velocity-independent criterion for superfluid turbulence. Nature 424, 1022–1025.CrossRefGoogle ScholarPubMed
Geurst, J. A. 1988 Drift mass, multifluid modelling of two-phase bubbly flow and superfluid hydrodynamics. Phys. A Stat. Mech. Appl. 152, 1–28.CrossRefGoogle Scholar
Glaberson, W. I., Johnson, W. W. & Ostermeier, R. M. 1974 Instability of a vortex array in He II. Phys. Rev. Lett. 33, 1197–1200.CrossRefGoogle Scholar
Glampedakis, K., Andersson, N. & Samuelsson, L. 2011 Magnetohydrodynamics of superfluid and superconducting neutron star cores. Mon. Not. R. Astron. Soc. 410, 805–829.CrossRefGoogle Scholar
Gravitational Wave International Committee, 2012 URL: https://gwic.ligo.org/.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge Monographs on Mechanics and Applied Mathematics, Cambridge University Press, xii+328 pp.Google Scholar
Greenspan, H. P. & Howard, L. N. 1963 On a time-dependent motion of a rotating fluid. J. Fluid Mech. 17, 385–404.Google Scholar
Henderson, K. L. & Barenghi, C. F. 2000 The anomalous motion of superfluid helium in a rotating cavity. J. Fluid Mech. 406, 199–219.CrossRefGoogle Scholar
Henderson, K. L. & Barenghi, C. F. 2004 Superfluid Couette flow in an enclosed annulus. Theor. Comput. Fluid Dyn. 18, 183–196.CrossRefGoogle Scholar
Henderson, K. L., Barenghi, C. F. & Jones, C. A. 1995 Nonlinear Taylor–Couette flow of helium II. J. Fluid Mech. 283, 329–340.CrossRefGoogle Scholar
Hills, R. N. & Roberts, P. H. 1977 Superfluid mechanics for a high density of vortex lines. Arch. Rat. Mech. Anal. 66, 43–71.CrossRefGoogle Scholar
Hollerbach, R. 2003 Instabilities of the Stewartson layer. Part 1. The dependence on the sign of Ro . J. Fluid Mech. 492, 289–302.CrossRefGoogle Scholar
Hollerbach, R. 2009 Instabilities of Taylor columns in a rotating stratified fluid. Phys. Lett. A 373, 3775–3778.CrossRefGoogle Scholar
Ishii, M. & Mishima, K. 1984 Two fluid model and hydrodynamic constitutive relations. Nucl. Engng Des. 82, 107–126.CrossRefGoogle Scholar
Khalatnikov, I. M. 1965 Introduction to the Theory of Superfluidity. Benjamin.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1959 Fluid mechanics. In Course of Theoretical Physics. Pergamon.Google Scholar
Link, B., Epstein, R. I. & van Riper, K. A. 1992 Pulsar glitches as probes of neutron star interiors. Nature 359, 616–618.Google Scholar
Loper, D. E. 1971 Hydromagnetic spin-up of a fluid confined by two flat electrically conducting boundaries. J. Fluid Mech. 50, 609–623.CrossRefGoogle Scholar
Lyne, A. G., Shemar, S. L. & Smith, F. G. 2000 Statistical studies of pulsar glitches. Mon. Not. R. Astron. Soc. 315, 534–542.CrossRefGoogle Scholar
Melatos, A., Peralta, C. & Wyithe, J. S. B. 2008 Avalanche dynamics of radio pulsar glitches. Astrophys. J. 672, 1103–1118.CrossRefGoogle Scholar
Mendell, G. 1991a Superfluid hydrodynamics in rotating neutron stars. Part 1. Nondissipative equations. Astrophys. J. 380, 515–529.CrossRefGoogle Scholar
Mendell, G. 1991b Superfluid hydrodynamics in rotating neutron stars. Part 2. Dissipative effects. Astrophys. J. 380, 530–540.CrossRefGoogle Scholar
Onsager, L. 1931 Reciprocal relations in irreversible processes. Part 1. Phys. Rev. 37, 405–426.CrossRefGoogle Scholar
Paoletti, M. S. & Lathrop, D. P. 2011 Quantum turbulence. Annu. Rev. Condens. Matter Phys. 2, 213–234.CrossRefGoogle Scholar
Pedlosky, J. 1967 The spin up of a stratified fluid. J. Fluid Mech. 28, 463–479.CrossRefGoogle Scholar
Peradzynski, Z., Filipkowski, S. & Fiszdon, W. 1990 Spin-up of He II in a cylindrical vessel of finite height. Eur. J. Mech. B 9, 259–272.Google Scholar
Peralta, C., Melatos, A., Giacobello, M. & Ooi, A. 2005 Global three-dimensional flow of a neutron superfluid in a spherical shell in a neutron star. Astrophys. J. 635, 1224–1232.Google Scholar
Peralta, C., Melatos, A., Giacobello, M. & Ooi, A. 2006 Transitions between turbulent and laminar superfluid vorticity states in the outer core of a neutron star. Astrophys. J. 651, 1079–1091.CrossRefGoogle Scholar
Peralta, C., Melatos, A., Giacobello, M. & Ooi, A. 2008 Superfluid spherical Couette flow. J. Fluid Mech. 609, 221–274.Google Scholar
Reisenegger, A. 1993 The spin-up problem in Helium II. J. Low Temp. Phys. 92, 77–106.CrossRefGoogle Scholar
Skrbek, L. & Sreenivasan, K. R. 2012 Developed quantum turbulence and its decay. Phys. Fluids 24 (1), 011301.Google Scholar
Tsakadze, J. S. & Tsakadze, S. J. 1972 Relaxation phenomena at acceleration of rotation of a spherical vessel with helium II and relaxation in pulsars. Phys. Lett. A 41, 197–199.CrossRefGoogle Scholar
Tsakadze, J. S. & Tsakadze, S. J. 1973 Measurement of the relaxation time on acceleration of vessels with helium II and superfluidity in pulsars. Sov. J. Expl Theoret. Phys. 37, 918–921.Google Scholar
Tsakadze, J. S. & Tsakadze, S. J. 1974 On the problem of relaxation time determination in superfluids when their rotation is accelerated. Phys. Lett. A 47, 477–478.CrossRefGoogle Scholar
Tsakadze, J. S. & Tsakadze, S. J. 1980 Properties of slowly rotating helium II and the superfluidity of pulsars. J. Low Temp. Phys. 39, 649–688.CrossRefGoogle Scholar
Tsubota, M. 2009 Quantum turbulence: from superfluid helium to atomic Bose–Einstein condensates. J. Phys.: Condens. Matter 21 (16), 164207.Google ScholarPubMed
Tsubota, M., Barenghi, C. F., Araki, T. & Mitani, A. 2004 Instability of vortex array and transitions to turbulence in rotating helium II. Phys. Rev. B 69 (13), 134515.Google Scholar
Ungarish, M. 1990 Spin-up from rest of a mixture. Phys. Fluids 2, 160–166.Google Scholar
van Eysden, C. A. & Melatos, A. 2008 Gravitational radiation from pulsar glitches. Class. Quant. Grav. 25 (22), 225020.CrossRefGoogle Scholar
van Eysden, C. A. & Melatos, A. 2010 Pulsar glitch recovery and the superfluidity coefficients of bulk nuclear matter. Mon. Not. R. Astron. Soc. 409, 1253–1268.Google Scholar
van Eysden, C. A. & Melatos, A. 2011 Spin down of superfluid-filled vessels: theory versus experiment. J. Low Temp. Phys. 165, 1–14.Google Scholar
van Eysden, C. A. & Melatos, A. 2012 Interpreting superfluid spin up through the response of the container. J. Low Temp. Phys. 166, 151–170.Google Scholar
Vinen, W. F. 2010 Quantum turbulence: achievements and challenges. J. Low Temp. Phys. 161, 419–444.CrossRefGoogle Scholar
Vinen, W. F. & Niemela, J. J. 2002 Quantum turbulence. J. Low Temp. Phys. 128, 167–231.Google Scholar
Walin, G. 1969 Some aspects of time-dependent motion of a stratified rotating fluid. J. Fluid Mech. 36, 289–307.Google Scholar
Walmsley, P. M., Golov, A. I., Hall, H. E., Levchenko, A. A. & Vinen, W. F. 2007 Dissipation of quantum turbulence in the zero temperature limit. Phys. Rev. Lett. 99 (26), 265302.Google Scholar
Wang, N., Manchester, R. N., Pace, R. T., Bailes, M., Kaspi, V. M., Stappers, B. W. & Lyne, A. G. 2000 Glitches in southern pulsars. Mon. Not. R. Astron. Soc. 317, 843–860.CrossRefGoogle Scholar
Warszawski, L. & Melatos, A. 2013 Knock-on processes in superfluid vortex avalanches and pulsar glitch statistics. Mon. Not. R. Astron. Soc. 428, 1911–1926.Google Scholar
Warszawski, L., Melatos, A. & Berloff, N. G. 2012 Unpinning triggers for superfluid vortex avalanches. Phys. Rev. B 85 (10), 104503.CrossRefGoogle Scholar
Wedemeyer, E. H. 1964 The unsteady flow within a spinning cylinder. J. Fluid Mech. 20, 383–399.Google Scholar
Zwillinger, D. 1989 Handbook of Differential Equations. Academic.Google Scholar