Published online by Cambridge University Press: 02 December 2022
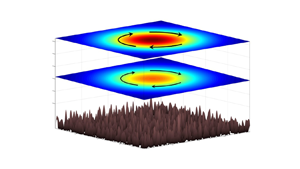
This study explores the impact of small-scale variability in the bottom relief on the dynamics and evolution of broad baroclinic flows in the ocean. The analytical model presented here generalizes the previously reported barotropic ‘sandpaper’ theory of flow–topography interaction to density-stratified systems. The multiscale asymptotic analysis leads to an explicit representation of the large-scale effects of irregular bottom roughness. The utility of the multiscale model is demonstrated by applying it to the problem of topography-induced spin-down of an axisymmetric vortex. We find that bathymetry affects vortices by suppressing circulation in their deep regions. As a result, vortices located above rough topography tend to be more stable than their flat-bottom counterparts. The multiscale theory is validated by comparing corresponding topography-resolving and parametric simulations.