Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T15:39:08.446Z Has data issue: false hasContentIssue false
  • English
  • Français

Spatio-temporal proper orthogonal decomposition of turbulent channel flow

Published online by Cambridge University Press:  11 February 2019

Srikanth Derebail Muralidhar ,
Bérengère Podvin Open the ORCID record for Bérengère Podvin [Opens in a new window] ,
Lionel Mathelin Open the ORCID record for Lionel Mathelin [Opens in a new window]  and
Yann Fraigneau
Srikanth Derebail Muralidhar
Affiliation:
LIMSI, CNRS, Université Paris-Saclay, 91403 Orsay CEDEX, France
Bérengère Podvin*
Affiliation:
LIMSI, CNRS, Université Paris-Saclay, 91403 Orsay CEDEX, France
Lionel Mathelin
Affiliation:
LIMSI, CNRS, Université Paris-Saclay, 91403 Orsay CEDEX, France Department of Applied Mathematics, University of Washington, Seattle, WA 98105, USA
Yann Fraigneau
Affiliation:
LIMSI, CNRS, Université Paris-Saclay, 91403 Orsay CEDEX, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

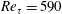An extension of proper orthogonal decomposition is applied to the wall layer of a turbulent channel flow ($Re_{\unicode[STIX]{x1D70F}}=590$), so that empirical eigenfunctions are defined in both space and time. Due to the statistical symmetries of the flow, the eigenfunctions are associated with individual wavenumbers and frequencies. Self-similarity of the dominant eigenfunctions, consistent with wall-attached structures transferring energy into the core region, is established. The most energetic modes are characterized by a fundamental time scale in the range 200–300 viscous wall units. The full spatio-temporal decomposition provides a natural measure of the convection velocity of structures, with a characteristic value of 12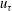$u_{\unicode[STIX]{x1D70F}}$ in the wall layer. Finally, we show that the energy budget can be split into specific contributions for each mode, which provides a closed-form expression for nonlinear effects.

JFM classification

Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 864 , 10 April 2019 , pp. 614 - 639
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alamo, J. C. D. & Jimenez, J. 2009 Estimation of turbulent convection velocities and corrections to Taylor’s approximation. J. Fluid Mech. 640, 5–26.Google Scholar
Alamo, J. C. D., Jimenez, J., Zandonade, P. & Moser, R. D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.Google Scholar
Arndt, R. E. A., Long, D. F. & Glauser, M. N. 1997 The proper orthogonal decomposition of pressure surrounding a turbulent jet. J. Fluid Mech. 340, 1–33.Google Scholar
Aubry, N., Holmes, P., Lumley, J. L. & Stone, E. 1988 The dynamics of coherent structures in the wall region of the wall boundary layer. J. Fluid Mech. 192, 115–173.10.1017/S0022112088001818Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.10.1146/annurev.fl.25.010193.002543Google Scholar
Blackwelder, R. F. & Haritodinis, J. H. 1983 Scaling of the bursting frequency in turbulent boundary layers. J. Fluid Mech. 132, 87–103.Google Scholar
Chen, K. K., Tu, J. H. & Rowley, C. W. 2012 Variants of dynamic mode decomposition: boundary condition, Koopman, and Fourier analyses. J. Nonlinear Sci. 22 (6), 887–915.10.1007/s00332-012-9130-9Google Scholar
Choi, K. S., Debisschop, J. R. & Clayton, B. R. 1998 Turbulent boundary layer control by means of spanwise wall oscillations. AIAA J. 36 (7), 1157–1163.10.2514/2.526Google Scholar
Citriniti, J. & George, W. 2000 Reconstruction of the global velocity field in the axisymmetric mixing layer utilizing the proper orthogonal decomposition. J. Fluid Mech. 418, 137–166.Google Scholar
Corino, E. R. & Brodkey, R. S. 1969 A visual investigation of the wall region in turbulent flow. J. Fluid Mech. 37, 1–30.10.1017/S0022112069000395Google Scholar
Delville, J., Ukeiley, L., Cordier, L., Bonnet, J. P. & Glauser, M. 1999 Examination of large-scale structures in a turbulent plane mixing layer. Part 1. Proper orthogonal decomposition. J. Fluid Mech. 391, 91–122.Google Scholar
Dennis, D. J. C. 2015 Coherent structures in wall-bounded turbulence. Anais da Academia Brasileira de Ciencias 87, 1161–1193.Google Scholar
Frisch, U. 1995 Turbulence. Cambridge University Press.Google Scholar
Gatski, M. & Glauser, M. 1992 Proper orthogonal decomposition based turbulence modeling. In Instability, Transition and Turbulence (ed. Hussaini, M. Y., Kumar, A. & Streett, C. L.), Springer.Google Scholar
George, W. K. 2017 A 50-year retrospective and the future. In Whither Turbulence and Big Data in the 21st Century? pp. 13–43. Springer.Google Scholar
Glauser, M. N. & George, W. K. 1987 An orthogonal decomposition of the axisymmetric jet mixing layer utilizing cross-wire measurements. In Proceedings of the Sixth Symposium on Turbulent Shear Flow, Springer.Google Scholar
Glauser, M. N., Leib, S. J. & George, W. K. 1983 An application of Lumley’s orthogonal decomposition to the axisymmetric jet mixing layer. In Bulletin of American Physical Society, DFD Annual Meeting, American Physical Society.Google Scholar
Halko, N., Martinsson, P. G. & Tropp, J. A. 2011 Finding structure with randomness: probabilistic algorithms for constructing approximate matrix decompositions. SIAM Rev. 53 (2), 217–288.Google Scholar
Hamilton, J. M., Kim, J. & Waleffe, F. 1995 Regeneration mechanisms of near-wall turbulence structures. J. Fluid Mech. 287, 317–348.Google Scholar
Hong, S. K. & Rubesin, M. W.1985 Application of large-eddy interaction model to channel flow. NASA Tech. Mem. 86691.Google Scholar
Jiménez, J. 2013 Near-wall turbulence. Phys. Fluids 25 (10), 101302.Google Scholar
Jimenez, J. & Moin, P. 1991 The minimal flow unit in near-wall turbulence. J. Fluid Mech. 225, 213–240.Google Scholar
Kannan, R. & Vempala, S. 2017 Randomized algorithms in numerical linear algebra. Acta Numer. 26, 95–135.Google Scholar
Kim, H. T., Kline, S. J. & Reynolds, W. C. 1971 The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 50 (1), 133–160.10.1017/S0022112071002490Google Scholar
Kreplin, H. P. & Eckelmann, H. 1979 Propagation of perturbations in the viscous sublayer and adjacent wall region. J. Fluid Mech. 95, 305–322.10.1017/S0022112079001488Google Scholar
Krogstad, P. A., Kaspersen, J. H. & Rinestead, S. 1998 Convection velocities in a turbulent boundary layer. Phys. Fluids 10, 949–957.10.1063/1.869617Google Scholar
Loève, M. 1977 Probability Theory. Springer.Google Scholar
Lumley, J. L. 1965 On the interpretation of temporal spectra in high intensity shear flows. Phys. Fluids 8, 1056–1062.Google Scholar
Lumley, J. L. 1967 The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation, pp. 221–227. Nauka.Google Scholar
McKeon, B. J. 2017 The engine behind (wall) turbulence: perspectives on scale interactions. J. Fluid Mech. 817, P1.Google Scholar
Mezić, I. 2005 Spectral properties of dynamical systems, model reduction and decompositions. Nonlinear Dyn. 41 (1), 309–325.Google Scholar
Moin, P. & Moser, R. D. 1989 Characteristic-eddy decomposition of turbulence in a channel. J. Fluid Mech. 200, 471–509.10.1017/S0022112089000741Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to Re 𝜏 = 590. Phys. Fluids 11 (4), 943–945.10.1063/1.869966Google Scholar
Podvin, B. 2001 On the adequacy of the ten-dimensional model for the wall layer. Phys. Fluids 13 (1), 210–224.10.1063/1.1328741Google Scholar
Podvin, B. & Fraigneau, Y. 2014 POD-based wall boundary conditions for the numerical simulation of turbulent channel flows. J. Turbul. 15 (3), 145–171.Google Scholar
Podvin, B. & Fraigneau, Y. 2017 A few thoughts on proper orthogonal decomposition in turbulence. Phys. Fluids 29, 020709.Google Scholar
Podvin, B., Fraigneau, Y., Jouanguy, J. & Laval, J. P. 2010 On self-similarity in the inner wall layer of a turbulent channel flow. J. Fluids Engng 132 (4), 41202.Google Scholar
Podvin, B. & Lumley, J. L. 1998 A low-dimensional approach for the minimal flow unit. J. Fluid Mech. 362, 121–155.Google Scholar
Quadrizio, M. & Ricco, P. 2004 Critical assessment of drag reduction through spanwise wall oscillations. J. Fluid Mech. 521, 251–271.10.1017/S0022112004001855Google Scholar
Robinson, S. K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.Google Scholar
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.Google Scholar
Ruiz-Antolín, D. & Townsend, A. 2018 A nonuniform fast Fourier transform based on low rank approximation. SIAM J. Sci. Comput. 40 (1), A529–A547.Google Scholar
Schmid, P. J. 2010 Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 656, 5–28.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part 1. Coherent structures. Q. J. Mech. Appl. Maths 45, 561–571.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43 (1), 353–375.10.1146/annurev-fluid-122109-160753Google Scholar
Stanislas, M., Jimenez, J. & Marusic, I.(Eds) 2011 Progress in Wall Turbulence: Understanding and Modeling, Springer.10.1007/978-90-481-9603-6Google Scholar
Stanislas, M., Perret, L. & Foucaut, J. M. 2008 Vortical structures in the turbulent boundary layer: a possible route to a universal representation. J. Fluid Mech. 602, 327–382.Google Scholar
Towne, A., Schmidt, O. & Colonius, T. 2018 Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 847, 821–867.Google Scholar
Townsend, A. A. 1976 The Structure of Turbulent Shear Flow. Cambridge University Press.Google Scholar
Ukeiley, L., Cordier, L., Manceau, R., Delville, J., Glauser, M. & Bonnet, J. 2001 Examination of large-scale structures in a turbulent plane mixing layer. Part 2. Dynamical systems model. J. Fluid Mech. 441, 67–108.Google Scholar
Wallace, J. M. 2014 Space–time correlations in turbulent flow: a review. Theor. Appl. Mech. Lett. 4, 0022003.10.1063/2.1402203Google Scholar
Westerwheel, J., Elsinga, G. E. & Adrian, R. J. 2013 Particle image velocimetry for complex and turbulent flows. Annu. Rev. Fluid Mech. 45, 409–436.Google Scholar
Zhou, J.1993 Interacting scales and energy transfer in isotropic turbulence. Tech. Rep. CR-191477, NASA.Google Scholar