Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T02:16:48.437Z Has data issue: false hasContentIssue false
  • English
  • Français

Spatial and spectral characteristics of information flux between turbulent boundary layers and porous media

Published online by Cambridge University Press:  23 September 2022

Wenkang Wang Open the ORCID record for Wenkang Wang [Opens in a new window] ,
Adrián Lozano-Durán Open the ORCID record for Adrián Lozano-Durán [Opens in a new window] ,
Rainer Helmig  and
Xu Chu Open the ORCID record for Xu Chu [Opens in a new window]
Wenkang Wang
Affiliation:
Max Planck Institute for Intelligent Systems, 70569 Stuttgart, Germany Institute for Modelling Hydraulic and Environmental Systems , University of Stuttgart, 70569 Stuttgart, Germany
Adrián Lozano-Durán
Affiliation:
Department of Aeronautics and Astronautics, Massachusetts Institute of Technology, Cambridge, MA 021139, USA
Rainer Helmig
Affiliation:
Institute for Modelling Hydraulic and Environmental Systems , University of Stuttgart, 70569 Stuttgart, Germany
Xu Chu*
Affiliation:
Cluster of Excellence SimTech, University of Stuttgart, 70569 Stuttgart, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

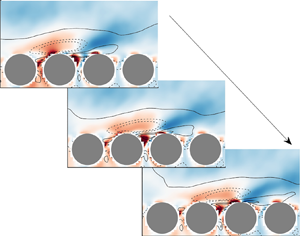
The interaction between boundary layer turbulence and a porous layer is the cornerstone of interface engineering. In this study, the spatial and spectral-resolved transfer entropy is used to assess the asymmetry of the causal interaction next to the permeable wall. The analysis is based on pore-resolved direct numerical simulation of turbulent channel flow over cylinder arrays. The spatial map of transfer entropy reveals the information flux between the porous medium and arbitrary nearby positions, and paths connecting locations with maximum information transfer are identified. The paths in the ‘top-down’ and ‘bottom-up’ directions, respectively, lean upstream and downstream, demonstrating that the coupling process is directionally dependent. The scale dependence of transfer entropy is inspected with a surrogate data strategy. As wall permeability increases, the active scale range in causal interaction shifts from near-wall vortices to Kelvin–Helmholtz type eddies. In addition, linear stochastic estimation is used to determine the statistical velocity field for a local informative event. In an average sense, the interaction between a convecting sweep or ejection event and the up/down-welling motions at the pore unit is the core mechanism that contributes to the causal coupling. The statistical findings derived from the transfer entropy are then validated using a neural network-based remote sensing model.

JFM classification

Turbulent Flows: Turbulent boundary layers Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 949 , 25 October 2022 , A16
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abderrahaman-Elena, N. & García-Mayoral, R. 2017 Analysis of anisotropically permeable surfaces for turbulent drag reduction. Phys. Rev. Fluids 2 (11), 114609.CrossRefGoogle Scholar
Adrian, R.J. & Moin, P. 1988 Stochastic estimation of organized turbulent structure: homogeneous shear flow. J. Fluid Mech. 190, 531–559.CrossRefGoogle Scholar
Besserve, M., Schölkopf, B., Logothetis, N.K. & Panzeri, S. 2010 Causal relationships between frequency bands of extracellular signals in visual cortex revealed by an information theoretic analysis. J. Comput. Neurosci. 29 (3), 547–566.CrossRefGoogle ScholarPubMed
Bottaro, A. 2019 Flow over natural or engineered surfaces: an adjoint homogenization perspective. J. Fluid Mech. 877, P1.CrossRefGoogle Scholar
Breakspear, M., Brammer, M. & Robinson, P.A. 2003 Construction of multivariate surrogate sets from nonlinear data using the wavelet transform. Physica D 182 (1), 1–22.CrossRefGoogle Scholar
Breugem, W.P., Boersma, B.J. & Uittenbogaard, R.E. 2006 The influence of wall permeability on turbulent channel flow. J. Fluid Mech. 562, 35–72.CrossRefGoogle Scholar
Cantwell, C.D., Sherwin, S.J., Kirby, R.M. & Kelly, P.H.J. 2011 From h to p efficiently: strategy selection for operator evaluation on hexahedral and tetrahedral elements. Comput. Fluids 43 (1), 23–28.CrossRefGoogle Scholar
Chu, X., Wang, W., Yang, G., Terzis, A., Helmig, R. & Weigand, B. 2021 Transport of turbulence across permeable interface in a turbulent channel flow: interface-resolved direct numerical simulation. Transp. Porous Media 136 (1), 165–189.CrossRefGoogle Scholar
Chu, X., Wu, Y., Rist, U. & Weigand, B. 2020 Instability and transition in an elementary porous medium. Phys. Rev. Fluids 5 (4), 044304.CrossRefGoogle Scholar
Chu, X., Yang, G., Pandey, S. & Weigand, B. 2019 Direct numerical simulation of convective heat transfer in porous media. Intl J. Heat Mass Transfer 133, 11–20.CrossRefGoogle Scholar
Encinar, M.P. & Jiménez, J. 2019 Logarithmic-layer turbulence: a view from the wall. Phys. Rev. Fluids 4, 114603.CrossRefGoogle Scholar
Fang, H., Xu, H., He, G. & Dey, S. 2018 Influence of permeable beds on hydraulically macro-rough flow. J. Fluid Mech. 847, 552–590.CrossRefGoogle Scholar
Finnigan, J. 2000 Turbulence in plant canopies. Annu. Rev. Fluid Mech. 32 (1), 519–571.CrossRefGoogle Scholar
Finnigan, J.J., Shaw, R.H. & Patton, E.G. 2009 Turbulence structure above a vegetation canopy. J. Fluid Mech. 637, 387–424.CrossRefGoogle Scholar
Gómez-de Segura, G. & García-Mayoral, R. 2019 Turbulent drag reduction by anisotropic permeable substrates–analysis and direct numerical simulations. J. Fluid Mech. 875, 124–172.CrossRefGoogle Scholar
Gourévitch, B. & Eggermont, J.J. 2007 Evaluating information transfer between auditory cortical neurons. J. Neurophysiol. 97 (3), 2533–2543.CrossRefGoogle ScholarPubMed
Guastoni, L., Guemes, A., Ianiro, A., Discetti, S., Schlatter, P., Azizpour, H. & Vinuesa, R. 2021 Convolutional-network models to predict wall-bounded turbulence from wall quantities. J. Fluid Mech. 928, A27.CrossRefGoogle Scholar
Hosseini, Z., Martinuzzi, R.J. & Noack, B.R. 2016 Modal energy flow analysis of a highly modulated wake behind a wall-mounted pyramid. J. Fluid Mech. 798, 717–750.CrossRefGoogle Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.CrossRefGoogle Scholar
Jeong, J., Hussain, F., Schoppa, W. & Kim, J. 1997 Coherent structures near the wall in a turbulent channel flow. J. Fluid Mech. 332, 185–214.CrossRefGoogle Scholar
Jiménez, J., Uhlmann, M., Pinelli, A. & Kawahara, G. 2001 Turbulent shear flow over active and passive porous surfaces. J. Fluid Mech. 442, 89–117.CrossRefGoogle Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.CrossRefGoogle Scholar
Jodai, Y. & Elsinga, G.E. 2016 Experimental observation of hairpin auto-generation events in a turbulent boundary layer. J. Fluid Mech. 795, 611–633.CrossRefGoogle Scholar
Karniadakis, G.E., Israeli, M. & Orszag, S.A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97 (2), 414–443.CrossRefGoogle Scholar
Karniadakis, G.E., Karniadakis, G. & Sherwin, S. 2005 Spectral/hp Element Methods For Computational Fluid Dynamics. Oxford University Press on Demand.CrossRefGoogle Scholar
Karra, S.K., Apte, S.V., He, X. & Scheibe, T.D. 2022 Pore-resolved simulations of turbulent boundary layer flow over permeable and impermeable sediment beds. arXiv:2204.13875.Google Scholar
Kim, T., Blois, G., Best, J.L. & Christensen, K.T. 2018 Experimental study of turbulent flow over and within cubically packed walls of spheres: effects of topography, permeability and wall thickness. Intl J. Heat Fluid Flow 73, 16–29.CrossRefGoogle Scholar
Kim, T., Blois, G., Best, J.L. & Christensen, K.T. 2020 Experimental evidence of amplitude modulation in permeable-wall turbulence. J. Fluid Mech. 887, A3.CrossRefGoogle Scholar
Kim, J. & Lee, C. 2020 Prediction of turbulent heat transfer using convolutional neural networks. J. Fluid Mech. 882, A18.CrossRefGoogle Scholar
Kooij, G.L., Botchev, M.A., Frederix, E.M.A., Geurts, B.J., Horn, S., Lohse, D., van der Poel, E.P., Shishkina, O., Stevens, R.J.A.M. & Verzicco, R. 2018 Comparison of computational codes for direct numerical simulations of turbulent Rayleigh–Bénard convection. Comput. Fluids 166, 1–8.CrossRefGoogle Scholar
Kuwata, Y. & Suga, K. 2016 Lattice Boltzmann direct numerical simulation of interface turbulence over porous and rough walls. Intl J. Heat Fluid Flow 61, 145–157.CrossRefGoogle Scholar
Kuwata, Y. & Suga, K. 2017 Direct numerical simulation of turbulence over anisotropic porous media. J. Fluid Mech. 831, 41–71.CrossRefGoogle Scholar
Lizier, J.T., Prokopenko, M. & Zomaya, A.Y. 2012 Local measures of information storage in complex distributed computation. Inf. Sci. 208, 39–54.CrossRefGoogle Scholar
Lozano-Durán, A. & Arranz, G. 2022 Information-theoretic formulation of dynamical systems: causality, modeling, and control. Phys. Rev. Res. 4, 023195.CrossRefGoogle Scholar
Lozano-Durán, A., Bae, H.J. & Encinar, M.P. 2020 Causality of energy-containing eddies in wall turbulence. J. Fluid Mech. 882, A2.CrossRefGoogle Scholar
Lozano-Durán, A., Constantinou, N.C., Nikolaidis, M.-A. & Karp, M. 2021 Cause-and-effect of linear mechanisms sustaining wall turbulence. J. Fluid Mech. 914, A8.CrossRefGoogle Scholar
Manes, C., Poggi, D. & Ridolfi, L. 2011 Turbulent boundary layers over permeable walls: scaling and near wall structure. J. Fluid Mech. 687, 141–170.CrossRefGoogle Scholar
Manes, C., Pokrajac, D., McEwan, I. & Nikora, V. 2009 Turbulence structure of open channel flows over permeable and impermeable beds: a comparative study. Phys. Fluids 21 (12), 125109.CrossRefGoogle Scholar
McCorquodale, M.W. & Munro, R.J. 2021 Direct effects of boundary permeability on turbulent flows: observations from an experimental study using zero-mean-shear turbulence. J. Fluid Mech. 915, A134.CrossRefGoogle Scholar
McCulloch, W.S. & Pitts, W. 1943 A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 5 (4), 115–133.CrossRefGoogle Scholar
Moin, P. & Mahesh, K. 1998 Direct numerical simulation: a tool in turbulence research. Annu. Rev. Fluid Mech. 30 (1), 539–578.CrossRefGoogle Scholar
Motlagh, S.Y. & Taghizadeh, S. 2016 Pod analysis of low Reynolds turbulent porous channel flow. Intl J. Heat Fluid Flow 61, 665–676.CrossRefGoogle Scholar
Nepf, H.M. 2012 Flow and transport in regions with aquatic vegetation. Annu. Rev. Fluid Mech. 44, 123–142.CrossRefGoogle Scholar
Pandey, S., Chu, X., Weigand, B., Laurien, E. & Schumacher, J. 2020 Relaminarized and recovered turbulence under nonuniform body forces. Phys. Rev. Fluids 5 (10), 104604.CrossRefGoogle Scholar
Percival, D.B. & Walden, A.T. 2000 Wavelet Methods for Time Series Analysis, vol. 4. Cambridge University Press.CrossRefGoogle Scholar
Pinzuti, E., Wollstadt, P., Gutknecht, A., Tüscher, O. & Wibral, M. 2020 Measuring spectrally-resolved information transfer. PLoS Comput. Biol. 16 (12), e1008526.CrossRefGoogle ScholarPubMed
Raissi, M., Perdikaris, P. & Karniadakis, G.E. 2019 Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707.CrossRefGoogle Scholar
Rosti, M.E., Brandt, L. & Pinelli, A. 2018 Turbulent channel flow over an anisotropic porous wall–drag increase and reduction. J. Fluid Mech. 842, 381–394.CrossRefGoogle Scholar
Rosti, M.E., Cortelezzi, L. & Quadrio, M. 2015 Direct numerical simulation of turbulent channel flow over porous walls. J. Fluid Mech. 784, 396–442.CrossRefGoogle Scholar
Schreiber, T. 2000 Measuring information transfer. Phys. Rev. Lett. 85, 461–464.CrossRefGoogle ScholarPubMed
Shen, G., Yuan, J. & Phanikumar, M.S. 2020 Direct numerical simulations of turbulence and hyporheic mixing near sediment water interfaces. J. Fluid Mech. 892, A20.CrossRefGoogle Scholar
Srinivasan, P.A., Guastoni, L., Azizpour, H., Schlatter, P. & Vinuesa, R. 2019 Predictions of turbulent shear flows using deep neural networks. Phys. Rev. Fluids 4 (5), 054603.CrossRefGoogle Scholar
Suga, K., Nakagawa, Y. & Kaneda, M. 2017 Spanwise turbulence structure over permeable walls. J. Fluid Mech. 822, 186–201.CrossRefGoogle Scholar
Suga, K., Okazaki, Y., Ho, U. & Kuwata, Y. 2018 Anisotropic wall permeability effects on turbulent channel flows. J. Fluid Mech. 855, 983–1016.CrossRefGoogle Scholar
Suga, K., Okazaki, Y. & Kuwata, Y. 2020 Characteristics of turbulent square duct flows over porous media. J. Fluid Mech. 884, A7.CrossRefGoogle Scholar
Terzis, A., Zarikos, I., Weishaupt, K., Yang, G., Chu, X., Helmig, R. & Weigand, B. 2019 Microscopic velocity field measurements inside a regular porous medium adjacent to a low Reynolds number channel flow. Phys. Fluids 31 (4), 042001.CrossRefGoogle Scholar
Theobald, F., Schäfer, K., Yang, J., Frohnapfel, B., Stripf, M., Forooghi, P. & Stroh, A. 2021 Comparison of different solvers and geometry representation strategies for DNS of rough wall channel flow. In 14th WCCM-ECCOMAS Congress 2020 (ed. F. Chinesta, R. Abgrall, O. Allix & M. Kaliske), vol. 600. KITopen.CrossRefGoogle Scholar
Voermans, J.J., Ghisalberti, M. & Ivey, G.N. 2017 The variation of flow and turbulence across the sediment–water interface. J. Fluid Mech. 824, 413–437.CrossRefGoogle Scholar
Wang, W., Chu, X., Lozano-Durán, A., Helmig, R. & Weigand, B. 2021 a Information transfer between turbulent boundary layer and porous media. J. Fluid Mech. 920, A21.CrossRefGoogle Scholar
Wang, W., Pan, C. & Wang, J. 2021 b Energy transfer structures associated with large-scale motions in a turbulent boundary layer. J. Fluid Mech. 906, A14.CrossRefGoogle Scholar
Wang, W., Yang, G., Evrim, C., Terzis, A., Helmig, R. & Chu, X. 2021 c An assessment of turbulence transportation near regular and random permeable interfaces. Phys. Fluids 33 (11), 115103.CrossRefGoogle Scholar
White, B.L. & Nepf, H.M. 2007 Shear instability and coherent structures in shallow flow adjacent to a porous layer. J. Fluid Mech. 593, 1–32.CrossRefGoogle Scholar
Wibral, M., Pampu, N., Priesemann, V., Siebenhühner, F., Seiwert, H., Lindner, M., Lizier, J.T. & Vicente, R. 2013 Measuring information-transfer delays. PLoS One 8 (2), e55809.CrossRefGoogle ScholarPubMed
Wu, S., Christensen, K.T. & Pantano, C. 2020 A study of wall shear stress in turbulent channel flow with hemispherical roughness. J. Fluid Mech. 885, A16.CrossRefGoogle Scholar
Xu, H.H.A., Altland, S.J., Yang, X.I.A. & Kunz, R.F. 2021 Flow over closely packed cubical roughness. J. Fluid Mech. 920, A37.CrossRefGoogle Scholar
Yuan, J. & Aghaei Jouybari, M. 2018 Topographical effects of roughness on turbulence statistics in roughness sublayer. Phys. Rev. Fluids 3, 114603.CrossRefGoogle Scholar