Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-26T17:22:14.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Some insights for the prediction of near-wall turbulence

Published online by Cambridge University Press:  16 April 2013

Farid Karimpour  and
Subhas K. Venayagamoorthy
Farid Karimpour
Affiliation:
Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, CO 80523-1372, USA
Subhas K. Venayagamoorthy*
Affiliation:
Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, CO 80523-1372, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we revisit the eddy viscosity formulation to highlight a number of important issues that have direct implications for the prediction of near-wall turbulence. For steady wall-bounded turbulent flows, we make the equilibrium assumption between rates of production (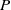$P$) and dissipation ($\epsilon $) of turbulent kinetic energy (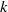$k$) in the near-wall region to propose that the eddy viscosity should be given by 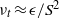${\nu }_{t} \approx \epsilon / {S}^{2} $, where 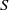$S$ is the mean shear rate. We then argue that the appropriate velocity scale is given by 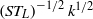$\mathop{(S{T}_{L} )}\nolimits ^{- 1/ 2} {k}^{1/ 2} $ where 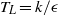${T}_{L} = k/ \epsilon $ is the turbulence (decay) time scale. The difference between this velocity scale and the commonly assumed velocity scale of 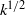${k}^{1/ 2} $ is subtle but the consequences are significant for near-wall effects. We then extend our discussion to show that the fundamental length and time scales that capture the near-wall behaviour in wall-bounded shear flows are the shear mixing length scale 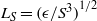${L}_{S} = \mathop{(\epsilon / {S}^{3} )}\nolimits ^{1/ 2} $ and the mean shear time scale 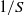$1/ S$, respectively. With these appropriate length and time scales (or equivalently velocity and time scales), the eddy viscosity can be rewritten in the familiar form of the 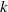$k$–$\epsilon $ model as 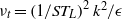${\nu }_{t} = \mathop{(1/ S{T}_{L} )}\nolimits ^{2} {k}^{2} / \epsilon $. We use the direct numerical simulation (DNS) data of turbulent channel flow of Hoyas & Jiménez (Phys. Fluids, vol. 18, 2006, 011702) and the turbulent boundary layer flow of Jiménez et al. (J. Fluid Mech. vol. 657, 2010, pp. 335–360) to perform ‘a priori’ tests to check the validity of the revised eddy viscosity formulation. The comparisons with the exact computations from the DNS data are remarkable and highlight how well the equilibrium assumption holds in the near-wall region. These findings could prove to be useful in near-wall modelling of turbulent flows.

JFM classification

Turbulent Flows: Turbulent boundary layers Mixing: Turbulent mixing Turbulent Flows: Turbulence modelling
Type
Papers
Information
Journal of Fluid Mechanics , Volume 723 , 25 May 2013 , pp. 126 - 139
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C., Jiménez, J., Zandonade, J. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.CrossRefGoogle Scholar
Corrsin, S. 1958 Local isotropy in turbulent shear flow. NACA RM 58B11.Google Scholar
van Driest, E. R. 1956 On turbulent flow near a wall. J. Aero. Sci. 23, 1007–1011.CrossRefGoogle Scholar
Durbin, P. A. 1991 Near-wall turbulence closure modelling without damping functions. Theor. Comput. Fluid Dyn. 3, 1–13.Google Scholar
Durbin, P. A. & Pettersson Reif, B. A. 2011 Statistical Theory and Modelling for Turbulent Flows. John Wiley and Sons.Google Scholar
Gad-el-Hak, M. & Bandyopadhyay, P. R. 1994 Reynolds number effects in wall-bounded turbulent flows. Appl. Mech. Rev. 47, 307–365.CrossRefGoogle Scholar
George, W. K. 2007 Is there a universal log law for turbulent wall-bounded flows?. Phil. Trans. R. Soc. Lond. A 365, 789–806.Google Scholar
Hanjalić, K. & Launder, B. E. 1976 Contribution towards a Reynolds-stress closure for low-Reynolds-number turbulence. J. Fluid Mech. 74, 593–610.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $R{e}_{\tau } = 2003$ . Phys. Fluids 18, 011702.CrossRefGoogle Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.CrossRefGoogle Scholar
Jiménez, J., Hoyas, S., Simens, M. P. & Mizuno, Y. 2010 Turbulent boundary layers and channels at moderate Reynolds numbers. J. Fluid Mech. 657, 335–360.Google Scholar
Jiménez, J. & Moser, R. D. 2007 What are we learning from simulating wall turbulence?. Phil. Trans. R. Soc. Lond. A 365, 715–732.Google ScholarPubMed
Jones, M. B., Nickels, T. B. & Marusic, I. 2008 On the asymptotic similarity of the zero-pressure-gradient turbulent boundary layer. J. Fluid Mech. 616, 195–203.Google Scholar
Jones, W. P. & Launder, B. E. 1973 The calculation of low-Reynolds-number phenomena with a two-equation model of turbulence. Intl J. Heat Mass Transfer 16, 1119–1130.Google Scholar
Kalitzin, G., Medic, G., Iaccarino, G. & Durbin, P. 2005 Near-wall behaviour of RANS turbulence models and implications for wall functions. J. Comput. Phys. 204, 265–291.CrossRefGoogle Scholar
Kawai, S. & Larsson, J. 2012 Wall-modelling in large eddy simulation: length scales, grid resolution, and accuracy. Phys. Fluids 24, 015105.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.CrossRefGoogle Scholar
Lam, C. K. G. & Bremhorst, K. A. 1981 A modified form of the $k- \epsilon $ model for predicting wall turbulence. Trans. ASME I: J. Fluids Engng 103, 456–460.Google Scholar
Launder, B. E. & Spalding, D. B. 1972 Mathematical Models of Turbulence. Academic Press.Google Scholar
Loulou, P., Moser, R. D., Mansour, N. N. & Cantwell, B. J. 1997 Direct numerical simulation of incompressible pipe flow using B-spline spectral method. NASA Tech. Mem. 110436.Google Scholar
Marusic, I., McKeon, B. J., Monkewitz, P. A., Nagib, H. M., Smits, A. J. & Sreenivasan, K. R. 2010 Wall-bounded turbulent flows at high Reynolds numbers: recent advances and key issues. Phys. Fluids 22, 065103.Google Scholar
McKeon, B. J., Li, J., Jiang, W., Morrison, J. F. & Smits, A. J. 2004 Further observations on the mean velocity distribution in fully developed pipe flow. J. Fluid Mech. 501, 135–147.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to $R{e}_{\tau } = 590$ . Phys. Fluids 11, 943–945.Google Scholar
Patel, V. C., Rodi, W. & Scheuerer, G. 1985 Turbulence models for near-wall and low-Reynolds-number flows: a review. AIAA J. 23, 1308–1319.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Rahman, M. M. & Siikonen, T. 2005 An eddy viscosity model with near-wall modifications. Int. J. Numer. Meth. Fluids 49, 975–997.Google Scholar
Rodi, W. & Mansour, N. N. 1993 Low Reynolds number $k$ - $\epsilon $ modelling with the aid of direct numerical simulation data. J. Fluid Mech. 250, 509–529.Google Scholar
Smits, A. J., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Venayagamoorthy, S. K. & Stretch, D. D. 2010 On the turbulent Prandtl number in homogeneous stably stratified turbulence. J. Fluid Mech. 644, 359–369.Google Scholar
Wilson, J. D. 2012 An alternative eddy-viscosity model for the horizontally uniform atmospheric boundary layer. Boundary-Layer Meteorol. 45, 165–184.Google Scholar
Wu, X. & Moin, P. 2008 A direct numerical simulation study on the mean velocity characteristics in turbulent pipe flow. J. Fluid Mech. 608, 81–112.Google Scholar
Zagarola, M. V. & Smits, A. J. 1998 Mean-flow scaling of turbulent pipe flow. J. Fluid Mech. 373, 33–79.Google Scholar