Article contents
Solitary waves perturbed by a broad sill. Part 2. Propagation along the sill
Published online by Cambridge University Press: 26 November 2019
Abstract
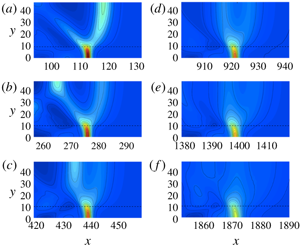
Evolution of a solitary wave travelling along a submerged sill is studied. The disturbance from the sill creates a phase lag along the wave crest between the ambient water depth and the shallower depth over the sill. This phase lag causes wave diffraction between the different parts of the wave, which induces radiating waves off the edge of the sill. The radiating waves act as an outlet for wave energy, resulting in significant and continual amplitude reduction of the solitary wave. Findings from laboratory experiments are confirmed numerically by simulating a much longer propagation distance with different sill breadths. When the sill breadth is narrow, the solitary wave slowly attenuates by wave radiation, maintaining a quasi-steady wave pattern. This is not the case for a broader sill. The resulting phase lag on the sill continually changes the wave pattern and the attenuation rate is substantially greater than the rate for the case of the narrow sill. The significant energy radiation together with the continual change in the wave formation eventually leads to the complete annihilation of the solitary wave in a wave tank. We also report a wave-breaking process along the sill observed in laboratory experiments. This breaking is induced when the wave amplitude on the sill is smaller than the maximum amplitude of a solitary wave in a uniform depth. Also found is the wake-like formation of gravity–capillary waves behind the breaking crest forming on the sill. Other features associated with the breaking are presented.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 2
- Cited by


