Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-17T16:00:51.143Z Has data issue: false hasContentIssue false
  • English
  • Français

Slip-induced suppression of Marangoni film thickening in surfactant-retarded Landau–Levich–Bretherton flows

Published online by Cambridge University Press:  24 September 2015

David Halpern ,
Yen-Ching Li  and
Hsien-Hung Wei
David Halpern
Affiliation:
Department of Mathematics, University of Alabama, Tuscaloosa, AL 35487, USA
Yen-Ching Li
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
Hsien-Hung Wei*
Affiliation:
Department of Chemical Engineering, National Cheng Kung University, Tainan 701, Taiwan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We report that the well-known Marangoni film thickening in surfactant-laden Landau–Levich–Bretherton coating flow can be completely suppressed by wall slip. The analysis is made by mainly looking at how the deposited film thickness varies with the capillary number 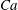$Ca$ (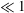$\ll 1$) and the dimensionless slip length 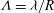${\it\Lambda}={\it\lambda}/R$ (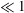$\ll 1$) in the presence of a trace amount of insoluble surfactant, where 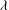${\it\lambda}$ is the slip length and 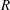$R$ is the radius of the meniscus. When slip effects are weak at sufficiently large $Ca$ (but still 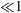$\ll 1$) such that 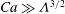$Ca\gg {\it\Lambda}^{3/2}$, the film thickness can still vary as 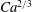$Ca^{2/3}$ and be thickened by surfactant as if wall slip were absent. However, when slip effects become strong by lowering 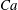$Ca$ to 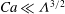$Ca\ll {\it\Lambda}^{3/2}$, the film, especially when surface diffusion of surfactant is negligible, does not get thinner according to the strong-slip quadratic law reported previously (Liao et al., Phys. Rev. Lett., vol. 111, 2013, 136001; Li et al., J. Fluid Mech., vol. 741, 2014, pp. 200–227). Instead, the film behaves as if both surfactant and wall slip were absent, precisely following the no-slip 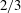$2/3$ law without surfactant. Effects of surface diffusion are also examined, revealing three distinct regimes as $Ca$ is varied from small to large values: the strong-slip quadratic scaling without surfactant, the no-slip 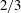$2/3$ scaling without surfactant and the film thickening along the no-slip $2/3$ scaling with surfactant. An experiment is also suggested to test the above findings.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface) Low-Reynolds-number flows: Lubrication theory Interfacial Flows (free surface): Thin films
Type
Papers
Information
Journal of Fluid Mechanics , Volume 781 , 25 October 2015 , pp. 578 - 594
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bretherton, F. P. 1961 The motion of long bubbles in tubes. J. Fluid Mech. 10 (2), 166–188.Google Scholar
Campanella, O. H. & Cerro, R. L. 1984 Viscous flow on the outside of a horizontal rotating cylinder: the roll coating regime with a single fluid. Chem. Engng Sci. 39 (10), 1443–1449.Google Scholar
Choi, C.-H. & Kim, C.-J. 2006 Large slip of aqueous liquid flow over a nanoengineered superhydrophobic surface. Phys. Rev. Lett. 96 (6), 066001.Google Scholar
Delacotte, J., Montel, L., Restagno, F., Scheid, B., Dollet, B., Stone, H. A., Langevin, D. & Rio, E. 2012 Plate coating: influence of concentrated surfactants on the film thickness. Langmuir 28 (8), 3821–3830.CrossRefGoogle ScholarPubMed
de Gennes, P. G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57 (3), 827–863.Google Scholar
Hindmarsh, A. C. 1983 ODEPACK, a systematized collection of ODE solvers. In Scientific Computing (ed. Stepleman, R. S., Carver, M., Peskin, R., Ames, W. F. & Vichnevetsky, R.), IMACS Transactions on Scientific Computation, vol. 1, pp. 55–64. North-Holland.Google Scholar
Kalliadasis, S. & Chang, H.-C. 1994 Apparent dynamic contact angle of an advancing gas–liquid meniscus. Phys. Fluids 6 (1), 12–23.Google Scholar
Krechetnikov, R. & Homsy, G. M. 2006 Surfactant effects in the Landau–Levich problem. J. Fluid Mech. 559, 429–450.Google Scholar
Landau, L. & Levich, B. 1942 Dragging of a liquid by a moving plate. Acta Physicochim. USSR 17, 42–54.Google Scholar
Li, Y.-C., Liao, Y.-C., Wen, T.-C. & Wei, H.-H. 2014 Breakdown of the Bretherton law due to wall slippage. J. Fluid Mech. 741, 200–227.Google Scholar
Liao, Y.-C., Li, Y.-C., Chang, Y.-C., Huang, C.-Y. & Wei, H.-H. 2014 Speeding up thermocapillary migration of a confined bubble by wall slip. J. Fluid Mech. 746, 31–52.Google Scholar
Liao, Y.-C., Li, Y.-C. & Wei, H.-H. 2013 Drastic changes in interfacial hydrodynamics due to wall slippage: slip-intensified film thinning, drop spreading, and capillary instability. Phys. Rev. Lett. 111, 136001.Google Scholar
Matthews, M. T. & Hill, J. M. 2009 On three simple experiments to determine slip lengths. Microfluid. Nanofluid. 6 (5), 611–619.Google Scholar
Park, C. W. 1991 Effects of insoluble surfactants on dip coating. J. Colloid Interface Sci. 146 (2), 382–394.CrossRefGoogle Scholar
Piroird, K., Clanet, C. & Quéré, D. 2011 Detergency in a tube. Soft Matt. 7 (16), 7498–7503.Google Scholar
Quéré, D. 1999 Fluid coating on a fiber. Annu. Rev. Fluid Mech. 31, 347–384.Google Scholar
Ramdane, O. O. & Quéré, D. 1997 Thickening factor in Marangoni coating. Langmuir 13 (11), 2911–2916.Google Scholar
Ratulowski, J. & Chang, H.-C. 1990 Marangoni effects of trace impurities on the motion of long gas-bubbles in capillaries. J. Fluid Mech. 210, 303–328.Google Scholar
Schwartz, L. W., Princen, H. M. & Kiss, A. D. 1986 On the motion of bubbles in capillary tubes. J. Fluid Mech. 172, 259–275.Google Scholar
Shen, A. Q., Gleason, B., McKinley, G. H. & Stone, H. A. 2002 Fiber coating with surfactant solutions. Phys. Fluids 14 (11), 4055–4068.Google Scholar
Stone, H. A. 1990 A simple derivation of the time-dependent convective-diffusion equation for surfactant transport. Phys. Fluids A 2 (1), 111–112.CrossRefGoogle Scholar
Stone, H. A. 2010 Interfaces: in fluid mechanics and across disciplines. J. Fluid Mech. 645, 1–25.Google Scholar
Wilson, S. D. R. 1982 The drag-out problem in film coating theory. J. Engng Maths 16 (3), 209–221.Google Scholar