Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T13:35:16.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Single-time Markovianized spectral closure in fluid turbulence

Published online by Cambridge University Press:  25 June 2020

Takuya Kitamura Open the ORCID record for Takuya Kitamura [Opens in a new window]
Takuya Kitamura*
Affiliation:
Graduate School of Engineering, Nagasaki University, Nagasaki852-8521, Japan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Kaneda’s (J. Fluid Mech., vol. 107, 1981, pp. 131–145) Lagrangian renormalized approximation was extended to single-time spectral closure under two assumptions: (i) Markovianization and (ii) the Lagrangian velocity response function is expressed by $G(k,\unicode[STIX]{x1D70F})=\exp (-C_{1}(k)\unicode[STIX]{x1D70F}-C_{2}(k)\unicode[STIX]{x1D70F}^{2}/2)$. 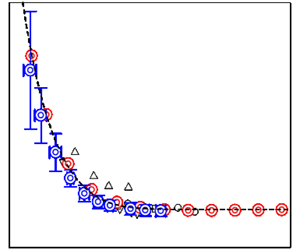The unknown functions $C_{1}(k)$ and $C_{2}(k)$ are theoretically derived to be consistent with the exact short-time behaviour of $G(k,\unicode[STIX]{x1D70F})$ and the asymptotic short-time behaviour of assumed exponential form of $G(k,\unicode[STIX]{x1D70F})$, i.e. the present closure is derived from the Navier–Stokes equation without introduction of any adjustable parameters and it can calculate the statistical quantities by theory. The results show that the present closure has good agreement with direct numerical simulation for single- and two-point statistics.

JFM classification

Turbulent Flows: Turbulence theory Turbulent Flows: Isotropic turbulence Turbulent Flows: Homogeneous turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 898 , 10 September 2020 , A8
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. & Stegun, I. A. 1964 Handbook of Mathematical Functions. Courier Corporation.Google Scholar
Antonia, R. A., Tang, S. L., Djenidi, L. & Danaila, L. 2015 Boundedness of the velocity derivative skewness in various turbulent flows. J. Fluid Mech. 781, 727–744.CrossRefGoogle Scholar
Armstrong, J. W., Rickett, B. J. & Spangler, S. R. 1995 Electron density power spectrum in the local interstellar medium. Astrophys. J. 443, 209–221.CrossRefGoogle Scholar
Bos, W. J. T. & Bertoglio, J. P. 2013 Lagrangian Markovianized field approximation for turbulence. J. Turbul. 14, 99–120.CrossRefGoogle Scholar
Bos, W. J. T., Clark, T. T. & Rubinstein, R. 2007a Small scale response and modeling of periodically forced turbulence. Phys. Fluids 19, 055107.CrossRefGoogle Scholar
Bos, W. J. T. & Fang, L. 2015 Dependence of turbulent advection on the Lagrangian correlation time. Phys. Rev. E 91, 043020.Google ScholarPubMed
Bos, W. J. T., Shao, L. & Bertoglio, J. P. 2007b Spectral imbalance and the normalized dissipation rate of turbulence. Phys. Fluids 15, 045101.Google Scholar
Briard, A., Gomez, T., Sagaut, P. & Memari, S. 2015 Passive scalar decay laws in isotropic turbulence: Prandtl number effects. J. Fluid Mech. 784, 274–303.CrossRefGoogle Scholar
Cao, N., Chen, S. & Doolen, G. D. 1999 Statistics and structures of pressure in isotropic turbulence. Phys. Fluids 11, 2235–2250.CrossRefGoogle Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Doering, C. R. & Foias, C. 2002 Energy dissipation in body-forced turbulence. J. Fluid Mech. 467, 289–306.CrossRefGoogle Scholar
Gotoh, T., Fukayama, D. & Nakano, T. 2002 Velocity field statistics in homogeneous steady turbulence obtained using a high-resolution direct numerical simulation. Phys. Fluids 14, 1065–1081.CrossRefGoogle Scholar
Gotoh, T. & Kaneda, Y. 2000 A numerical algorithm for efficiently solving spectral closure equations. In Advances in Turbulence VIII, pp. 693–696.Google Scholar
Gotoh, T., Kaneda, Y. & Bekki, N. 1988 Numerical integration of the Lagrangian renormalized approximation. J. Phys. Soc. Japan 57, 866–880.CrossRefGoogle Scholar
Gotoh, T., Nagaki, J. & Kaneda, Y. 2000 Passive scalar spectrum in the viscous-convective range in two-dimensional steady turbulence. Phys. Fluids 12, 155–168.CrossRefGoogle Scholar
Gradshteyn, I. S. & Ryzhik, I. M. 2014 Table of Integrals, Series, and Products. Academic.Google Scholar
Herring, J. R. 1965 Self-consistent-field approach to turbulence theory. Phys. Fluids 8, 2219–2225.CrossRefGoogle Scholar
Herring, J. R. & Kraichnan, R. H. 1979 A numerical comparison of velocity-based and strain-based Lagrangian-history turbulence approximations. J. Fluid Mech. 91, 581–597.CrossRefGoogle Scholar
Ishihara, T., Morishita, K., Yokokawa, M., Uno, A. & Kaneda, Y. 2016 Energy spectrum in high-resolution direct numerical simulations of turbulence. Phys. Rev. Fluids 1, 082403.CrossRefGoogle Scholar
Jiménez, J., Wray, A. A., Saffman, P. G. & Rogallo, R. S. 1993 The structure of intense vorticity in isotropic turbulence. J. Fluid Mech. 255, 65–90.CrossRefGoogle Scholar
Kaneda, Y. 1981 Renormalized expansions in the theory of turbulence with the use of Lagrangian position function. J. Fluid Mech. 107, 131–145.CrossRefGoogle Scholar
Kaneda, Y. 1993 Lagrangian and Eulerian time correlations in turbulence. Phys. Fluids 5, 2835–2845.CrossRefGoogle Scholar
Kaneda, Y., Ishihara, T., Yokokawa, M., Itakura, K. & Uno, A. 2003 Energy dissipation rate and energy spectrum in high resolution direct numerical simulations of turbulence in aperiodic box. Phys. Fluids 15, 21–24.CrossRefGoogle Scholar
Kida, S. & Goto, S. 1997 A Lagrangian direct-interaction approximation for homogeneous isotropic turbulence. J. Fluid Mech. 345, 307–345.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941a Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 15–17.Google Scholar
Kolmogorov, A. N. 1941b The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 31, 301–305.Google Scholar
Kraichnan, R. H. 1959 The structure of isotropic turbulence at very high Reynolds numbers. J. Fluid Mech. 5, 497–543.CrossRefGoogle Scholar
Kraichnan, R. H. 1965 Lagrangian history closure approximation for turbulence. Phys. Fluids 8, 575–595.CrossRefGoogle Scholar
Kraichnan, R. H. 1971 An almost-Markovian Galilean-invariant turbulence model. J. Fluid Mech. 47, 513–524.CrossRefGoogle Scholar
Kraichnan, R. H. 1977 Eulerian and Lagrangian renormalization in turbulence theory. J. Fluid Mech. 83, 349–374.CrossRefGoogle Scholar
Kraichnan, R. H. 1994 Anomalous scaling of a randomly advected passive scalar. Phys. Rev. Lett. 72, 1016–1019.CrossRefGoogle ScholarPubMed
Kraichnan, R. H. & Herring, J. R. 1978 A strain based Lagrangian history turbulence theory. J. Fluid Mech. 88, 355–367.CrossRefGoogle Scholar
Lesieur, M. & Ossia, S. 2000 3D isotropic turbulence at very high Reynolds numbers: EDQNM study. J. Turbul. 1, 1–25.Google Scholar
Leslie, D. C. 1973 Developments in the Theory of Turbulence. Oxford University Press.Google Scholar
Matthaeus, W. H. & Goldstein, L. 1982 Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res. 87, 6011–6028.CrossRefGoogle Scholar
McComb, W. D. 1989 The Physics of Fluid Turbulence. Clarendon Press.Google Scholar
McComb, W. D. 2014 Homogeneous, Isotropic Turbulence. Oxford University Press.CrossRefGoogle Scholar
McComb, W. D. & Shanmugasundaram, V. 1984 Numerical calculation of decaying isotropic turbulence using the LET theory. J. Fluid Mech. 143, 95–123.CrossRefGoogle Scholar
Monin, A. S. & Yaglom, A. M. 1975 Statistical Fluid Mechanics, vol. II. MIT Press.Google Scholar
Nastrom, G. D. & Gage, K. S. 1985 A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 42, 950–960.2.0.CO;2>CrossRefGoogle Scholar
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7, 2778–2784.CrossRefGoogle Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.CrossRefGoogle Scholar
Tsuji, Y. 2004 Intermittency effect on energy spectrum in high-Reynolds number turbulence. Phys. Fluids 16, L43–L46.CrossRefGoogle Scholar
Yoshida, K., Ishihara, T. & Kaneda, Y. 2003 Anisotropic spectrum of homogeneous turbulent shear flow in a Lagrangian renormalized approximation. Phys. Fluids 15, 2385–2397.CrossRefGoogle Scholar