Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Zonta, Francesco
and
Chibbaro, Sergio
2016.
Entropy production and Fluctuation Relation in turbulent thermal convection.
EPL (Europhysics Letters),
Vol. 114,
Issue. 5,
p.
50011.
Carbone, Francesco
Gencarelli, Christian N.
and
Hedgecock, Ian M.
2016.
Lagrangian statistics of mesoscale turbulence in a natural environment: The Agulhas return current.
Physical Review E,
Vol. 94,
Issue. 6,
Liot, Olivier
Gay, Amélie
Salort, Julien
Bourgoin, Mickaël
and
Chillà, Francesca
2016.
Inhomogeneity and Lagrangian unsteadiness in turbulent thermal convection.
Physical Review Fluids,
Vol. 1,
Issue. 6,
Zhang, Yang
Huang, Yong-Xiang
Jiang, Nan
Liu, Yu-Lu
Lu, Zhi-Ming
Qiu, Xiang
and
Zhou, Quan
2017.
Statistics of velocity and temperature fluctuations in two-dimensional Rayleigh-Bénard convection.
Physical Review E,
Vol. 96,
Issue. 2,
Ding, Da-Wei
Yan, Jie
Wang, Nian
and
Liang, Dong
2017.
Adaptive Synchronization of Fractional Order Complex-Variable Dynamical Networks via Pinning Control.
Communications in Theoretical Physics,
Vol. 68,
Issue. 3,
p.
366.
Liot, Olivier
Salort, Julien
Seychelles, Fanny
Gasteuil, Yoann
Pinton, Jean-François
and
Chillà, Francesca
2017.
Lagrangian Measurements in Turbulent Thermal Convection: About the Inhomogeneity of the Velocity and Temperature Fields.
Procedia IUTAM,
Vol. 20,
Issue. ,
p.
112.
Horstmann, G.M.
Schiepel, D.
and
Wagner, C.
2018.
Experimental study of the global flow-state transformation in a rectangular Rayleigh-Bénard sample.
International Journal of Heat and Mass Transfer,
Vol. 126,
Issue. ,
p.
1333.
Kim, Jin-Tae
Shen, Shikun
DiMarco, Steven L.
Jin, Yaqing
and
Chamorro, Leonardo P.
2018.
Lagrangian acceleration in Rayleigh-Bénard convection at various aspect ratios.
Physical Review Fluids,
Vol. 3,
Issue. 11,
Couston, Louis-Alexandre
Lecoanet, Daniel
Favier, Benjamin
and
Le Bars, Michael
2018.
The energy flux spectrum of internal waves generated by turbulent convection.
Journal of Fluid Mechanics,
Vol. 854,
Issue. ,
Liot, Olivier
Martin-Calle, David
Gay, Amélie
Salort, Julien
Chillà, Francesca
and
Bourgoin, Mickaël
2019.
Pair dispersion in inhomogeneous turbulent thermal convection.
Physical Review Fluids,
Vol. 4,
Issue. 9,
Duguid, Craig D
Barker, Adrian J
and
Jones, C A
2020.
Convective turbulent viscosity acting on equilibrium tidal flows: new frequency scaling of the effective viscosity.
Monthly Notices of the Royal Astronomical Society,
Vol. 497,
Issue. 3,
p.
3400.
Valori, Valentina
Innocenti, Alessio
Dubrulle, Bérengère
and
Chibbaro, Sergio
2020.
Weak formulation and scaling properties of energy fluxes in three-dimensional numerical turbulent Rayleigh–Bénard convection.
Journal of Fluid Mechanics,
Vol. 885,
Issue. ,
Pratt, Jane
Busse, Angela
and
Müller, Wolf-Christian
2020.
Lagrangian Statistics of Heat Transfer in Homogeneous Turbulence Driven by Boussinesq Convection.
Fluids,
Vol. 5,
Issue. 3,
p.
127.
Pratt, J.
Busse, A.
and
Müller, W.‐C.
2020.
Lagrangian Statistics for Dispersion in Magnetohydrodynamic Turbulence.
Journal of Geophysical Research: Space Physics,
Vol. 125,
Issue. 11,
Vidal, Jérémie
and
Barker, Adrian J
2020.
Efficiency of tidal dissipation in slowly rotating fully convective stars or planets.
Monthly Notices of the Royal Astronomical Society,
Vol. 497,
Issue. 4,
p.
4472.
Schiepel, Daniel
Schmeling, Daniel
and
Wagner, Claus
2021.
Simultaneous tomographic particle image velocimetry and thermometry of turbulent Rayleigh–Bénard convection.
Measurement Science and Technology,
Vol. 32,
Issue. 9,
p.
095201.
Machicoane, Nathanaël
and
Volk, Romain
2021.
Transport of large particles through the transition to turbulence of a swirling flow.
Physical Review Fluids,
Vol. 6,
Issue. 4,
Mommert, Michael
Niehaus, Konstantin
Schiepel, Daniel
Schmeling, Daniel
and
Wagner, Claus
2023.
Measurement of the turbulent heat fluxes in mixed convection using combined stereoscopic PIV and PIT.
Experiments in Fluids,
Vol. 64,
Issue. 6,
van Haren, Hans
2025.
Technical note: Spectral slopes in a deep, weakly stratified ocean and coupling between sub-mesoscale motion and small-scale mechanisms.
Ocean Science,
Vol. 21,
Issue. 2,
p.
555.
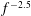 $f^{-2.5}$ frequency scaling, likely representing the ubiquitous passive and active scalar behaviour of temperature.
$f^{-2.5}$ frequency scaling, likely representing the ubiquitous passive and active scalar behaviour of temperature.