Article contents
Similarity of the two-dimensional and axisymmetric boundary-layer flows for purely viscous non-Newtonian fluids
Published online by Cambridge University Press: 28 March 2006
Extract
Conditions for the existence of similar solutions for the two-dimensional and axisymmetric boundary layers are obtained for the steady or unsteady flow for purely viscous non-Newtonian fluids, where the shear stress is proportional to the nth power of the velocity gradient and n > 0. These conditions are shown to be a generalization of the similarity conditions for Newtonian fluids. In particular it is found that the velocity at the outer edge of the boundary layer must be proportional to {R(x) + A}m or exp [AR(x)] for steady flows and to (t + A)m, (dx + A)/(t + B) or exp [At] for unsteady flows. Here x is the distance along the wall from the forward stagnation point, t is the time, R(x) = x for two-dimensional flows and 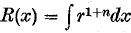 for axisymmetric flows, r is the distance from the axis to the wall, and A, B, d, m are constants.
for axisymmetric flows, r is the distance from the axis to the wall, and A, B, d, m are constants.
Several examples of the similar solutions are calculated analytically for both steady and unsteady pseudoplastic flows (n < 1). In these solutions the velocity in the boundary layer tends to the outside velocity in such a manner that the difference tends to zero as an inverse power of the distance from the wall, whereas such a difference tends to zero exponentially for the corresponding flow in Newtonian fluids.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1965
References
- 15
- Cited by


