Published online by Cambridge University Press: 08 June 2023
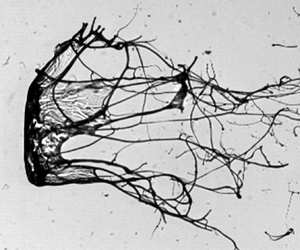
Droplet atomization through aerobreakup is omnipresent in various natural and industrial processes. Atomization of Newtonian droplets is a well-studied area; however, non-Newtonian droplets have received less attention despite their being frequently encountered. By subjecting polymeric droplets of different concentrations to the induced airflow behind a moving shock wave, we explore the role of elasticity in modulating the aerobreakup of viscoelastic droplets. Three distinct modes of aerobreakup are identified for a wide range of Weber number  $({\sim }10^2\unicode{x2013}10^4)$ and elasticity number
$({\sim }10^2\unicode{x2013}10^4)$ and elasticity number  $({\sim }10^{-4}\unicode{x2013}10^2)$ variation: these modes are vibrational, shear-induced entrainment and catastrophic breakup modes. Each mode is described as a three-stage process. Stage I is droplet deformation, stage II is the appearance and growth of hydrodynamic instabilities and stage III is the evolution of liquid mass morphology. It is observed that elasticity plays an insignificant role in the first two stages but a dominant role in the final stage. The results are described with the support of adequate mathematical analysis.
$({\sim }10^{-4}\unicode{x2013}10^2)$ variation: these modes are vibrational, shear-induced entrainment and catastrophic breakup modes. Each mode is described as a three-stage process. Stage I is droplet deformation, stage II is the appearance and growth of hydrodynamic instabilities and stage III is the evolution of liquid mass morphology. It is observed that elasticity plays an insignificant role in the first two stages but a dominant role in the final stage. The results are described with the support of adequate mathematical analysis.