Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-05T04:48:21.922Z Has data issue: false hasContentIssue false
  • English
  • Français

Shock waves in microchannels

Published online by Cambridge University Press:  29 April 2013

G. Mirshekari ,
M. Brouillette ,
J. Giordano ,
C. Hébert ,
J.-D. Parisse  and
P. Perrier
G. Mirshekari
Affiliation:
Department of Mechanical Engineering, Université de Sherbrooke, Sherbrooke, Quebec, Canada J1K 2R1
M. Brouillette*
Affiliation:
Department of Mechanical Engineering, Université de Sherbrooke, Sherbrooke, Quebec, Canada J1K 2R1
J. Giordano
Affiliation:
IUSTI UMR 7343 CNRS – Aix Marseille Université, 5 rue Enrico Fermi, 13453 Marseille, France
C. Hébert
Affiliation:
Department of Mechanical Engineering, Université de Sherbrooke, Sherbrooke, Quebec, Canada J1K 2R1
J.-D. Parisse
Affiliation:
IUSTI UMR 7343 CNRS – Aix Marseille Université, 5 rue Enrico Fermi, 13453 Marseille, France
P. Perrier
Affiliation:
IUSTI UMR 7343 CNRS – Aix Marseille Université, 5 rue Enrico Fermi, 13453 Marseille, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A fully instrumented microscale shock tube, believed to be the smallest to date, has been fabricated and tested. This facility is used to study the transmission of a shock wave, produced in a large (37 mm) shock tube, into a 34 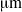$\mathrm{\mu} \mathrm{m} $ hydraulic diameter and 2 mm long microchannel. Pressure microsensors of a novel design, with gigahertz bandwidth, are used to obtain pressure–time histories of the microchannel shock wave at five axial stations. In all cases the transmitted shock wave is found to be weaker than the incident shock wave, and is observed to decay both in pressure and velocity as it propagates down the microchannel. These results are compared with various analytical and numerical models, and the best agreement is obtained with a Navier–Stokes computational fluid dynamics computation, which assumes a no-slip isothermal wall boundary condition; good agreement is also obtained with a simple shock tube laminar boundary layer model. It is also found that the flow developing within the microchannel is highly dependent on conditions at the microchannel entrance, which control the mass flux entering into the device. Regardless of the micrometre dimensions of the present facility, shock wave propagation in a microchannel of that scale exhibits a behaviour similar to that observed in large-scale facilities operated at low pressures, and the shock attenuation can be explained in terms of accepted laminar boundary models.

JFM classification

Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 724 , 10 June 2013 , pp. 259 - 283
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arkilic, E. B., Schmidt, M. A. & Breuer, K. S. 1997 Gaseous slip flow in long microchannels. J. Microelectromech. Syst. 6 (2), 167–178.CrossRefGoogle Scholar
Austin, J. & Bodony, D. J. 2011 Wave propagation in gaseous small-scale channel flows. Shock Waves 21 (6), 547–557.Google Scholar
Brouillette, M. 1991 Design modifications to T5 and their implementation. Tech. Rep. FM 91-3. Graduate Aeronautical Laboratories, California Institute of Technology.Google Scholar
Brouillette, M. 2003 Shock waves at microscales. Shock Waves 13 (1), 3–12.Google Scholar
Burtschell, Y., Cardoso, M. & Zeitoun, D. E. 2001 Numerical analysis of the reducing driver gas contamination in impulse shock tunnels. AIAA J. 12, 2357–2365.Google Scholar
Colin, S. 2005 Rarefaction and compressibility effects on steady and transient gas flows in microchannels. Microfluid Nanofluid 1 (8), 268–279.Google Scholar
Courant, R., Friedrichs, K. & Lewy, H. 1928 Über die partiellen differenzengleichungen der mathematischen physik. Math. Ann. 100 (1), 32–74.Google Scholar
Dolling, D. S. 2001 Fifty years of shock-wave/boundary-layer interaction research: What next? AIAA J. 39 (8), 1517–1531.CrossRefGoogle Scholar
Duff, R. E. 1959 Shock-tube performance at low initial pressure. Phys. Fluids 2 (2), 207–216.Google Scholar
Garen, W., Meyerer, B., Udagawa, S. & Maeno, K. 2009 Shock waves in mini-tubes: influence of the scaling parameter s. In Proceedings of 26th International Symposium on Shock Waves (ed. Hanneman, K. & Seiler, F.), pp. 1473–1478. Springer.Google Scholar
Giordano, J., Parisse, J. D. & Perrier, P. 2008 Numerical study of an original device to generate compressible flow in microchannels. Phys. Fluids 20, 096101.Google Scholar
Guo, Z.-Y. & Li, Z.-X. 2003 Size effect on microscale single-phase flow and heat transfer. Intl J. Heat Mass Transfer 46 (1), 149–159.Google Scholar
Iancu, F. & Muller, N. 2006 Efficiency of shock wave compression in a microchannel. Microfluid. Nanofluid. 2 (3), 50–63.Google Scholar
Kirchhoff, C. 1868 Ueber den einçuss der warmeleitung in einem gase auf die schallbewegung. Pogg. Ann. 134, 177–193.Google Scholar
Laporte, O. 1955 On the interaction of a shock with a constriction. Tech. Rep. LA-1740. Los Alamos Scientific Laboratory.Google Scholar
Lee, J. J., Frost, D. L., Lee, J. H. S. & Dremin, A. 1995 Propagation of nitromethane detonations in porous media. Shock Waves 5, 115–119.Google Scholar
Levy, A., Soreka, S., Ben-Dor, G. & Skews, B. 1996 Waves propagation in saturated rigid porous media: analytical model and comparison with experimental results. Fluid Dyn. Res. 17, 49–65.Google Scholar
Mahesh, K., Lele, S. K. & Moin, P. 1997 The influence of entropy fluctuations on the interaction of turbulence with a shock wave. J. Fluid Mech. 334, 353–379.Google Scholar
Martel, E. & Brouillette, M. 2003 Micro-blast waves at subatmospheric pressures. Comput. Fluid Dyn. 12 (2), 23–34.Google Scholar
Mirels, H. 1957 Attenuation in a shock tube due to unsteady-boundary-layer action. Tech. Rep. TN 1333. National Advisory Committee for Aeronautics.Google Scholar
Mirels, H. 1966 Correlation fomulas for laminar shock tube boundary layer. Phys. Fluids 9 (7), 1265–1272.Google Scholar
Mirshekari, G. 2008 Microscale shock tube. PhD thesis, University of Sherbrooke.Google Scholar
Mirshekari, G. & Brouillette, M. 2009 One-dimensional model for microscale shock tube flow. Shock Waves 19 (1), 25–38.Google Scholar
Mirshekari, G. & Brouillette, M. 2012 Microscale shock tube. J. Microelectromech. Syst. 99, 1–10.Google Scholar
Ngomo, D., Chaudhuri, A., Chinnayya, A. & Hadjadj, A. 2010 Numerical study of shock propagation and attenuation in narrow tubes including friction and heat losses. Comput. Fluids 39, 1711–1721.Google Scholar
Parisse, J. D., Giordano, J., Perrier, P., Burtschell, Y. & Graur, I. A. 2009 Numerical investigation of micro shock waves generation. Microfluid. Nanofluid. 6 (5), 699–709.Google Scholar
Quirk, J. J. 1998 Amrita—A computational facility (for CFD modelling). In VKI 29th CFD Lecture Series, von Kármán Institute for Fluid Dynamics, Brussels, 23–27 February 1998.Google Scholar
Roshko, A. 1960 On flow duration in low-pressure shock tubes. Phys. Fluids 3 (6), 835–842.Google Scholar
Russell, D. A. 1966 Shock-wave strengthening by area convergence. J. Fluid Mech. 27, 305–314.Google Scholar
Squires, T. M. & Quake, S. R. 2005 Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 77 (3), 977–1026.Google Scholar
Stewart, D. S. 2002 Towards the miniaturization of explosive technology. Shock Waves 11, 467–473.Google Scholar
Takayama, K. 1999 Applications of shock wave research to medicine. In Proceedings of 22nd International Symposium on Shock Waves (ed. G. J. Ball, R. Hillier & G. T. Roberts), pp. 321–326.Google Scholar
Udagawa, S., Garen, W., Meyerer, B. & Maeno, K. 2008 Motion analysis of a diaphragmless driver section for a narrow channel shock tube. Shock Waves 18 (5), 345–351.Google Scholar
Zeitoun, D. E. & Burtschel, Y. 2006 Navier-stokes computations in micro shock tubes. Shock Waves 15 (3–4), 241–246.Google Scholar