Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-06T06:17:30.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Shock wave–boundary layer interaction in supersonic flow over a forward-facing step

Published online by Cambridge University Press:  18 October 2016

Jayaprakash N. Murugan  and
Raghuraman N. Govardhan
Jayaprakash N. Murugan
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore 560 012, India
Raghuraman N. Govardhan*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Science, Bangalore 560 012, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study in the present work a Mach 2.5 flow over a forward-facing step. The focus of the work is the flow ahead of the step, in particular, the unsteady interactions between the shock, the boundary layer and the separation bubble. The primary geometrical parameter in the problem is the ratio of the step height to the incoming boundary layer thickness, 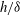$h/\unicode[STIX]{x1D6FF}$, which is kept fixed at 2. Results are presented from detailed particle image velocimetry (PIV) measurements in two orthogonal planes to obtain a reasonable picture of the whole flow field. The mean velocity field in the central cross-stream or wall-normal ($x$–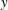$y$) plane shows that the incoming boundary layer separates upstream of the step forming a large separation bubble ahead of the step, which can be relatively well resolved in PIV measurements compared to the compression ramp cases. Wall pressure fluctuation spectra close to the separation location show a dominant frequency (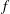$f$) that is two orders of magnitude smaller than the characteristic frequency of the incoming boundary layer (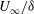$U_{\infty }/\unicode[STIX]{x1D6FF}$), consistent with low-frequency motions of the shock that have received a lot of recent attention (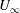$U_{\infty }$ $=$ free-stream velocity, 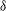$\unicode[STIX]{x1D6FF}$ $=$ boundary layer thickness). PIV measurements in the wall-normal plane show large variations in shock position with time. The shock position measured from velocity data outside the boundary layer is found to be well correlated with the reverse flow area ahead of the step, and weakly correlated to structures in the incoming boundary layer. In contrast, the shock foot, determined from velocity data within the boundary layer, is found to be well correlated to the low- and high-speed streaks in the incoming boundary layer, in addition to the reverse flow area ahead of the step. Instantaneous velocity fields in the spanwise ($x$–$z$) plane parallel to the lower wall show that the shock is broadly two-dimensional with small spanwise ripples, while the recirculation region has very large spanwise variations. The spanwise-averaged shock location is found to be well correlated to the most upstream location of the recirculation region over a spanwise length (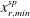$x_{r,min}^{sp}$). Instantaneous velocity fields show that when some part of the recirculation region is far upstream, the corresponding nearly two-dimensional shock is also far upstream. On the other hand, when 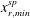$x_{r,min}^{sp}$ is relatively downstream, the resulting shock is also found to be downstream. Hence, the present results suggest that for the forward-facing step configuration, the large-scale streamwise motions of the shock are mainly correlated to the most upstream point of the recirculation region, which has large spanwise variations.

JFM classification

Boundary Layers: Boundary layer separation Aerodynamics: High-speed flow Compressible Flows: Shock waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 807 , 25 November 2016 , pp. 258 - 302
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Scientist Fellow, EAD, National Aerospace Laboratories, CSIR, Bangalore 560 017, India.

References

Adrian, R. J., Meinhart, C. D. & Tomkins, C. D. 2000 Vortex organization in the outer region of the turbulent boundary layer. J. Fluid Mech. 422, 1–54.Google Scholar
Andreopoulos, J. & Muck, K. C. 1987 Some new aspects of the shock-wave/boundary-layer interaction in compression-ramp flows. J. Fluid Mech. 180 (1), 405–428.Google Scholar
Andreopoulos, Y., Agui, J. H. & Briassulis, G. 2000 Shock wave-turbulence interactions. Annu. Rev. Fluid Mech. 32 (1), 309–345.CrossRefGoogle Scholar
Behrens, W.1971 Separation of a supersonic turbulent boundary layer by a forward-facing step. AIAA Paper 1971-0127.Google Scholar
Beresh, S. J., Clemens, N. T. & Dolling, D. S. 2002 Relationship between upstream turbulent boundary-layer velocity fluctuations and separation shock unsteadiness. AIAA J. 40 (12), 2412–2422.Google Scholar
Camussi, R., Felli, M., Pereira, F., Aloisio, G. & Di Marco, A. 2008 Statistical properties of wall pressure fluctuations over a forward-facing step. Phys. Fluids 20 (7), 075–113.CrossRefGoogle Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46 (1), 469–492.Google Scholar
Dolling, D. S. 2001 Fifty years of shock-wave/boundary-layer interaction research: what next? AIAA J. 39 (8), 1517–1531.Google Scholar
Dupont, P., Haddad, C. & Debiève, J. F. 2006 Space and time organization in a shock-induced separated boundary layer. J. Fluid Mech. 559, 255–277.Google Scholar
Dussauge, J. P., Dupont, P. & Debiève, J. F. 2006 Unsteadiness in shock wave boundary layer interactions with separation. Aero. Sci. Technol. 10 (2), 85–91.Google Scholar
Dussauge, J. P. & Piponniau, S. 2008 Shock/boundary-layer interactions: possible sources of unsteadiness. J. Fluids Struct. 24 (8), 1166–1175.Google Scholar
Elena, M. & LaCharme, J. P. 1988 Experimental study of a supersonic turbulent boundary layer using a laser doppler anemometer. J. Theor. Appl. Mech. 7 (2), 175–190.Google Scholar
Erengil, M. E. & Dolling, D. S. 1991 Unsteady wave structure near separation in a Mach 5 compression ramp interaction. AIAA J. 29 (5), 728–735.Google Scholar
Ganapathisubramani, B. 2007 Statistical properties of streamwise velocity in a supersonic turbulent boundary layer. Phys. Fluids 19 (9), 098108.CrossRefGoogle Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2006 Large-scale motions in a supersonic turbulent boundary layer. J. Fluid Mech. 556, 271–282.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2007 Effects of upstream boundary layer on the unsteadiness of shock-induced separation. J. Fluid Mech. 585, 369–394.Google Scholar
Ganapathisubramani, B., Clemens, N. T. & Dolling, D. S. 2009 Low-frequency dynamics of shock-induced separation in a compression ramp interaction. J. Fluid Mech. 636, 397–425.Google Scholar
Gran, R. L.1970 Step induced separation of a turbulent boundary layer. PhD thesis, California Institute of Technology.Google Scholar
Hou, Y. X.2003 Particle image velocimetry study of shock-induced turbulent boundary layer separation. PhD thesis, Department of Aerospace Engineering and Engineeering Mechanics, The University of Texas at Austin.CrossRefGoogle Scholar
Humble, R. A.2008 Unsteady flow organization of a shock wave/boundary layer interaction. PhD thesis, Faculty of Aerospace Engineering, Delft University of Technology, Delft, The Netherlands.Google Scholar
Humble, R. A., Elsinga, G. E., Scarano, F. & Van Oudheusden, B. W. 2009 Three-dimensional instantaneous structure of a shock wave/turbulent boundary layer interaction. J. Fluid Mech. 622, 33–62.CrossRefGoogle Scholar
Humble, R. A., Scarano, F. & Van Oudheusden, B. W. 2007 Particle image velocimetry measurements of a shock wave/turbulent boundary layer interaction. Exp. Fluids 43 (2–3), 173–183.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary layers. J. Fluid Mech. 579, 1–28.CrossRefGoogle Scholar
Kistler, A. L. 1964 Fluctuating wall pressure under a separated supersonic flow. J. Acoust. Soc. Am. 36, 543–550.Google Scholar
Klebanoff, P. S.1955 Characteristics of turbulence in a boundary layer with zero pressure gradient. NACA Tech. Rep. 1247, pp. 1135–1153.Google Scholar
Knight, D., Yan, H., Panaras, A. G. & Zheltovodov, A. 2003 Advances in CFD prediction of shock wave turbulent boundary layer interactions. Prog. Aerosp. Sci. 39 (2), 121–184.Google Scholar
Lanzerstorfer, D. & Kuhlmann, H. C. 2012 Three-dimensional instability of the flow over a forward-facing step. J. Fluid Mech. 695, 390–404.CrossRefGoogle Scholar
Larsson, J. & Lele, S. K. 2009 Direct numerical simulation of canonical shock/turbulence interaction. Phys. Fluids 21, 126101.Google Scholar
Lee, I., Ahn, S. K. & Sung, H. J. 2004 Three-dimensional coherent structure in a separated and reattaching flow over a backward-facing step. Exp. Fluids 36 (3), 373–383.Google Scholar
Marino, L. & Luchini, P. 2009 Adjoint analysis of the flow over a forward-facing step. Theor. Comput. Fluid Dyn. 23 (1), 37–54.Google Scholar
Martinuzzi, R. & Tropea, C. 1993 The flow around surface-mounted, prismatic obstacles placed in a fully developed channel flow. Trans. ASME J. Fluids Engng 115 (1), 85–92.Google Scholar
Melling, A. 1997 Tracer particles and seeding for particle image velocimetry. Meas. Sci. Technol. 8 (12), 1406–1416.Google Scholar
Moss, W. D. & Baker, S. 1980 Re-circulating flows associated with two-dimensional steps. Aeronaut. Q. 31, 151–172.Google Scholar
Pearson, D. S., Goulart, P. J. & Ganapathisubramani, B. 2013 Turbulent separation upstream of a forward-facing step. J. Fluid Mech. 724, 284–304.Google Scholar
Piponniau, S., Dussauge, J. P., Debiève, J. F. & Dupont, P. 2009 A simple model for low-frequency unsteadiness in shock-induced separation. J. Fluid Mech. 629, 87–108.CrossRefGoogle Scholar
Priebe, S. & Martin, M. P. 2012 Low-frequency unsteadiness in shock wave-turbulent boundary layer interaction. J. Fluid Mech. 699, 1–49.Google Scholar
Raffel, M. 2007 Particle Image Velocimetry: a Practical Guide. Springer.Google Scholar
Saric, W. S. 1994 Görtler vortices. Annu. Rev. Fluid Mech. 26 (1), 379–409.Google Scholar
Settles, G. S., Fitzpatrick, T. J. & Bogdonoff, S. M. 1979 Detailed study of attached and separated compression corner flowfields in high Reynolds number supersonic flow. AIAA J. 17 (6), 579–585.Google Scholar
Sherry, M., Jacono, D. L. & Sheridan, J. 2010 An experimental investigation of the recirculation zone formed downstream of a forward facing step. J. Wind Engng Ind. Aerodyn. 98 (12), 888–894.CrossRefGoogle Scholar
Sheu, T. W. H. & Rani, H. P. 2006 Exploration of vortex dynamics for transitional flows in a three-dimensional backward-facing step channel. J. Fluid Mech. 550, 61–83.Google Scholar
Smits, A. J. & Dussauge, J. P. 2006 Turbulent Shear Layers in Supersonic Flow. Springer.Google Scholar
Spall, R. E. & Malik, M. R. 1989 Görtler vortices in supersonic and hypersonic boundary layers. Phys. Fluids A 1 (11), 1822–1835.Google Scholar
Thomas, F. O., Putnam, C. M. & Chu, H. C. 1994 On the mechanism of unsteady shock oscillation in shock wave/turbulent boundary layer interactions. Exp. Fluids 18 (1–2), 69–81.CrossRefGoogle Scholar
Tomkins, C. D. & Adrian, R. J. 2003 Spanwise structure and scale growth in turbulent boundary layers. J. Fluid Mech. 490, 37–74.Google Scholar
Touber, E. & Sandham, N. D. 2009 Large-eddy simulation of low-frequency unsteadiness in a turbulent shock-induced separation bubble. Theor. Comput. Fluid Dyn. 23 (2), 79–107.Google Scholar
Unalmis, O. H. & Dolling, D. S. 1998 Experimental study of causes of unsteadiness of shock-induced turbulent separation. AIAA J. 36, 371–378.Google Scholar
Wilhelm, D., Härtel, C. & Kleiser, L. 2003 Computational analysis of the two-dimensional–three-dimensional transition in forward-facing step flow. J. Fluid Mech. 489, 1–27.Google Scholar
Wu, M. & Martin, M. P. 2008 Analysis of shock motion in shockwave and turbulent boundary layer interaction using direct numerical simulation data. J. Fluid Mech. 594, 71–83.Google Scholar
Zukoski, E. E. 1967 Turbulent boundary-layer separation in front of a forward-facing step. AIAA J. 5 (10), 1746–1753.Google Scholar