Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ulloa, Hugo N.
Constantinescu, George
Chang, Kyoungsik
Horna-Munoz, Daniel
Hames, Océane
and
Wüest, Alfred
2020.
Horizontal transport under wind-induced resonance in stratified waterbodies.
Physical Review Fluids,
Vol. 5,
Issue. 5,
Liu, Zihua
Grimshaw, Roger
and
Johnson, Edward
2021.
Resonant coupling of mode-1 and mode-2 internal waves by topography.
Journal of Fluid Mechanics,
Vol. 908,
Issue. ,
Hartharn-Evans, Samuel G.
Carr, Magda
Stastna, Marek
and
Davies, Peter A.
2022.
Stratification effects on shoaling internal solitary waves.
Journal of Fluid Mechanics,
Vol. 933,
Issue. ,
Wang, Zi’an
Wang, Zhan
and
Yuan, Chunxin
2022.
Oceanic internal solitary waves in three-layer fluids of great depth.
Acta Mechanica Sinica,
Vol. 38,
Issue. 2,
Ratliff, D J
2022.
Genuine nonlinearity and its connection to the modified Korteweg–de Vries equation in phase dynamics.
Nonlinearity,
Vol. 35,
Issue. 1,
p.
30.
Carr, Magda
Cuthbertson, Alan
and
Munro, Rick
2023.
Preface to the Special issue of Environmental Fluid Mechanics in Honour of Peter A. Davies.
Environmental Fluid Mechanics,
Vol. 23,
Issue. 2,
p.
185.
Li, Zhixin
Zhang, Meng
Liang, Keda
and
Wang, Jing
2023.
Optical remote sensing image characteristics of large amplitude convex mode-2 internal solitary waves: an experimental study.
Acta Oceanologica Sinica,
Vol. 42,
Issue. 6,
p.
16.
Stastna, Marek
Deepwell, David
and
Grace, Andrew
2023.
Shear instability in mode-2 internal Kelvin waves.
Environmental Fluid Mechanics,
Vol. 23,
Issue. 2,
p.
407.
Chesnokov, A. A.
Ermishina, V. E.
and
Liapidevskii, V. Yu.
2023.
Strongly non-linear Boussinesq-type model of the dynamics of internal solitary waves propagating in a multilayer stratified fluid.
Physics of Fluids,
Vol. 35,
Issue. 7,
Wang, Shaodong
Du, Hui
Wei, Gang
Peng, Pai
Xuan, Pu
and
Wang, Guanjing
2023.
Experimental investigation on the interaction between mode-2 internal solitary wave and horizontal transverse cylinder.
Physics of Fluids,
Vol. 35,
Issue. 8,
He, Xiao
Chen, Xu
Li, Qun
Xu, Tao
and
Meng, Jing
2023.
Numerical Simulations and an Updated Parameterization of the Breaking Internal Solitary Wave Over the Continental Shelf.
Journal of Geophysical Research: Oceans,
Vol. 128,
Issue. 11,
Yang, Adam J. K.
Olsthoorn, J.
and
Timmermans, M.-L.
2023.
Sedimentation in particle-laden flows with and without velocity shear.
Physics of Fluids,
Vol. 35,
Issue. 8,
Ellevold, Thea Josefine
Grue, John
and
Sletten, Joakim Soløy
2023.
Tracer particle motion driven by vortex formation in the bottom boundary layer underneath internal solitary waves.
Frontiers in Marine Science,
Vol. 10,
Issue. ,
Robinson, Edward
Hosegood, Phil
and
Bolton, Adam
2023.
Dynamical oceanographic processes impact on reef manta ray behaviour: Extreme Indian Ocean Dipole influence on local internal wave dynamics at a remote tropical atoll.
Progress in Oceanography,
Vol. 218,
Issue. ,
p.
103129.
Whitwell, C. A.
Jones, N. L.
Ivey, G. N.
Rosevear, M. G.
and
Rayson, M. D.
2024.
Ocean Mixing in a Shelf Sea Driven by Energetic Internal Waves.
Journal of Geophysical Research: Oceans,
Vol. 129,
Issue. 2,
Tong, Linlong
Zhang, Jisheng
Chen, Ning
Lin, Xiangfeng
He, Rui
and
Sun, Lei
2024.
Internal solitary wave-induced soil responses and its effects on seabed instability in the South China Sea.
Ocean Engineering,
Vol. 310,
Issue. ,
p.
118697.
Hartharn‐Evans, Samuel G.
Carr, Magda
and
Stastna, Marek
2024.
Interactions Between Internal Solitary Waves and Sea Ice.
Journal of Geophysical Research: Oceans,
Vol. 129,
Issue. 1,
Wang, Zi'an
Hu, Ganghua
and
Wang, Zhan
2024.
Dynamics of multi-mode nonlinear internal waves in fluids of great depth.
Physics of Fluids,
Vol. 36,
Issue. 4,
Wang, Shaodong
Du, Hui
Wei, Gang
Xu, Junnan
Peng, Pai
Xuan, Pu
and
Wang, Guanjing
2024.
Experimental Investigation on a convex Mode-2 internal solitary wave and its induced flow field.
Journal of Physics: Conference Series,
Vol. 2718,
Issue. 1,
p.
012044.
 $s$, is defined to be the height of the slope divided by the slope base length. In shallow slope cases (
$s$, is defined to be the height of the slope divided by the slope base length. In shallow slope cases (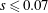 $s\leqslant 0.07$), the wave form is destroyed by the shoaling process; the leading mode-2 ISW degenerates into a train of mode-1 waves of elevation and little boundary layer activity is seen. For steeper slopes (
$s\leqslant 0.07$), the wave form is destroyed by the shoaling process; the leading mode-2 ISW degenerates into a train of mode-1 waves of elevation and little boundary layer activity is seen. For steeper slopes (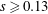 $s\geqslant 0.13$), boundary layer separation, vortex formation and re-suspension at the bed are observed. The boundary layer dynamics is shown (numerically) to be dependent on the Reynolds number of the flow. A reflected mode-2 wave signal and wave run up are seen for slopes of steepness
$s\geqslant 0.13$), boundary layer separation, vortex formation and re-suspension at the bed are observed. The boundary layer dynamics is shown (numerically) to be dependent on the Reynolds number of the flow. A reflected mode-2 wave signal and wave run up are seen for slopes of steepness 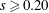 $s\geqslant 0.20$. The wave run up distance is shown to be proportional to the length scale
$s\geqslant 0.20$. The wave run up distance is shown to be proportional to the length scale 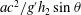 $ac^{2}/g^{\prime }h_{2}\sin \unicode[STIX]{x1D703}$ where
$ac^{2}/g^{\prime }h_{2}\sin \unicode[STIX]{x1D703}$ where 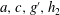 $a,c,g^{\prime },h_{2}$ and
$a,c,g^{\prime },h_{2}$ and 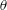 $\unicode[STIX]{x1D703}$ are wave amplitude, wave speed, reduced gravity, pycnocline thickness and slope angle respectively.
$\unicode[STIX]{x1D703}$ are wave amplitude, wave speed, reduced gravity, pycnocline thickness and slope angle respectively.


