Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T00:53:34.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Shear-induced collective diffusivity down a concentration gradient in a viscous emulsion of drops

Published online by Cambridge University Press:  03 April 2019

Abhilash Reddy Malipeddi  and
Kausik Sarkar Open the ORCID record for Kausik Sarkar [Opens in a new window]
Abhilash Reddy Malipeddi
Affiliation:
Department of Mechanical and Aerospace Engineering, The George Washington University, Washington, DC20052, USA
Kausik Sarkar*
Affiliation:
Department of Mechanical and Aerospace Engineering, The George Washington University, Washington, DC20052, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The shear-induced collective diffusivity down a concentration gradient in a viscous emulsion is computed using direct numerical simulation. A layer of randomly packed drops subjected to a shear flow, shows the layer width to increase with the 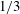$1/3$ power of time, consistent with a semi-dilute theory that assumes a diffusivity linear with concentration. This characteristic scaling and the underlying theory are used to compute the collective diffusivity coefficient. This is the first ever computation of this quantity for a system of deformable particles using fully resolved numerical simulation. The results match very well with previous experimental observations. The coefficient of collective diffusivity varies non-monotonically with the capillary number, due to the competing effects of increasing deformation and drop orientation. A phenomenological correlation for the collective diffusivity coefficient as a function of capillary number is presented. We also apply an alternative approach to compute collective diffusivity, developed originally for a statistically homogeneous rigid sphere suspension – computing the dynamic structure factor from the simulated droplet positions and examining its time variation at small wavenumber. We show that the results from this alternative approach qualitatively agree with our computation of collective diffusivity including the prediction of the non-monotonic variation of diffusivity with the capillary number.

JFM classification

Drops and Bubbles: Drops Complex Fluids: Emulsions Multiphase and Particle-laden Flows: Multiphase flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 868 , 10 June 2019 , pp. 5 - 25
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altenberger, A. R. 1979 On the wave vector dependent mutual diffusion of interacting Brownian particles. J. Chem. Phys. 70 (4), 1994–2002.Google Scholar
Altenberger, A. R. & Deutch, J. M. 1973 Light scattering from dilute macromolecular solutions. J. Chem. Phys. 59 (2), 894–898.Google Scholar
Batchelor, G. K. 1972 Sedimentation in a dilute dispersion of spheres. J. Fluid Mech. 52 (2), 245–268.Google Scholar
Batchelor, G. K. & Green, J. T. 1972 Determination of bulk stress in a suspension of spherical-particles to order C-2. J. Fluid Mech. 56 (Dec 12), 401–427.Google Scholar
Berne, B. J. & Pecora, R. 1976 Dynamic Light Scattering: With Applications to Chemistry, Biology, and Physics. Wiley.Google Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20 (1), 111–157.Google Scholar
Breedveld, L. V. A.2000 Shear-induced self-diffusion in concentrated suspensions. PhD thesis.Google Scholar
Breedveld, V., van den Ende, D., Tripathi, A. & Acrivos, A. 1998 The measurement of the shear-induced particle and fluid tracer diffusivities in concentrated suspensions by a novel method. J. Fluid Mech. 375, 297–318.Google Scholar
Bureau, L., Coupier, G., Dubois, F., Duperray, A., Farutin, A., Minetti, C., Misbah, C., Podgorski, T., Tsvirkun, D. & Vysokikh, M. 2017 Blood flow and microgravity. C. R. Méc. 345 (1), 78–85.Google Scholar
Cha, W. & Beissinger, R. L. 2001 Evaluation of shear-induced particle diffusivity in red cell ghosts suspensions. Korean J. Chem. Engng 18 (4), 479–485.Google Scholar
Chaffey, C. E. & Brenner, H. 1967 A second order theory for shear deformation of drops. J. Colloid Interface Sci. 24 (2), 258–269.Google Scholar
Chan, P. C. H. & Leal, L. G. 1979 The motion of a deformable drop in a second-order fluid. J. Fluid Mech. 92 (01), 131–170.Google Scholar
Cooke, B. M., Mohandas, N. & Coppel, R. L. 2001 The malaria-infected red blood cell: structural and functional changes. Adv. Parasitol. 50, 1–86.Google Scholar
da Cunha, F. & Hinch, E. J. 1996 Shear-induced dispersion in a dilute suspension of rough spheres. J. Fluid Mech. 309, 211–223.Google Scholar
Davis, R. H. 1996 Hydrodynamic diffusion of suspended particles: a symposium. J. Fluid Mech. 310, 325–335.Google Scholar
Desmond, K. & Weeks, E. 2009 Random close packing of disks and spheres in confined geometries. Phys. Rev. E 80 (5), 051305.Google Scholar
Eckstein, E. C., Bailey, D. G. & Shapiro, A. H. 1977 Self-diffusion of particles in shear flow of a suspension. J. Fluid Mech. 79 (01), 191–208.Google Scholar
Foss, D. R. & Brady, J. F. 1999 Self-diffusion in sheared suspensions by dynamic simulation. J. Fluid Mech. 401, 243–274.Google Scholar
Gires, P.-Y., Srivastav, A., Misbah, C., Podgorski, T. & Coupier, G. 2014 Pairwise hydrodynamic interactions and diffusion in a vesicle suspension. Phys. Fluids 26 (1), 013304.Google Scholar
Goldsmith, H. L. & Marlow, J. C. 1979 Flow behavior of erythrocytes. II. Particle motions in concentrated suspensions of ghost cells. J. Colloid Interface Sci. 71 (2), 383–407.Google Scholar
Grandchamp, X., Coupier, G., Srivastav, A., Minetti, C. & Podgorski, T. 2013 Lift and down-gradient shear-induced diffusion in red blood cell suspensions. Phys. Rev. Lett. 110 (10), 108101.Google Scholar
Higgins, J. M., Eddington, D. T., Bhatia, S. N. & Mahadevan, L. 2009 Statistical dynamics of flowing red blood cells by morphological image processing. PLOS Comput. Biol. 5 (2), e1000288.Google Scholar
Hudson, S. D. 2003 Wall migration and shear-induced diffusion of fluid droplets in emulsions. Phys. Fluids 15 (5), 1106–1113.Google Scholar
King, M. R. & Leighton, D. T. 2001 Measurement of shear-induced dispersion in a dilute emulsion. Phys. Fluids 13 (2), 397–406.Google Scholar
Leighton, D. T. & Acrivos, A. 1987 Measurement of shear-induced self-diffusion in concentrated suspensions of spheres. J. Fluid Mech. 177, 109–131.Google Scholar
Leshansky, A. M. & Brady, J. F. 2005 Dynamic structure factor study of diffusion in strongly sheared suspensions. J. Fluid Mech. 527, 141–169.Google Scholar
Leshansky, A. M., Morris, J. F. & Brady, J. F. 2008 Collective diffusion in sheared colloidal suspensions. J. Fluid Mech. 597, 305–341.Google Scholar
Li, X. & Sarkar, K. 2008 Front tracking simulation of deformation and buckling instability of a liquid capsule enclosed by an elastic membrane. J. Comput. Phys. 227 (10), 4998–5018.Google Scholar
Loewenberg, M. & Hinch, E. J. 1997 Collision of two deformable drops in shear flow. J. Fluid Mech. 338, 299–315.Google Scholar
Lopez, M. & Graham, M. D. 2008 Enhancement of mixing and adsorption in microfluidic devices by shear-induced diffusion and topography-induced secondary flow. Phys. Fluids 20 (5), 053304.Google Scholar
Marchioro, M. & Acrivos, A. 2001 Shear-induced particle diffusivities from numerical simulations. J. Fluid Mech. 443, 101–128.Google Scholar
Morris, J. F. & Brady, J. F. 1996 Self-diffusion in sheared suspensions. J. Fluid Mech. 312, 223–252.Google Scholar
Mukherjee, S. & Sarkar, K. 2009 Effects of viscosity ratio on deformation of a viscoelastic drop in a Newtonian matrix under steady shear. J. Non-Newtonian Fluid Mech. 160 (2–3), 104–112.Google Scholar
Mukherjee, S. & Sarkar, K. 2013 Effects of matrix viscoelasticity on the lateral migration of a deformable drop in a wall-bounded shear. J. Fluid Mech. 727, 318–345.Google Scholar
Mukherjee, S. & Sarkar, K. 2014 Lateral migration of a viscoelastic drop in a Newtonian fluid in a shear flow near a wall. Phys. Fluids 26 (10), 103102.Google Scholar
Olapade, P. O., Singh, R. K. & Sarkar, K. 2009 Pairwise interactions between deformable drops in free shear at finite inertia. Phys. Fluids 21 (6), 063302.Google Scholar
Podgorski, T., Callens, N., Minetti, C., Coupier, G., Dubois, F. & Misbah, C. 2011 Dynamics of vesicle suspensions in shear flow between walls. Microgravity Sci. Technol. 23 (2), 263–270.Google Scholar
Rallison, J. M. & Hinch, E. J. 1986 The effect of particle interactions on dynamic light scattering from a dilute suspension. J. Fluid Mech. 167, 131–168.Google Scholar
Ramachandran, A., Loewenberg, M. & Leighton, D. T. 2010 A constitutive equation for droplet distribution in unidirectional flows of dilute emulsions for low capillary numbers. Phys. Fluids 22 (8), 083301.Google Scholar
Rusconi, R. & Stone, H. A. 2008 Shear-induced diffusion of platelike particles in microchannels. Phys. Rev. Lett. 101, 254502.Google Scholar
Russel, W. B. & Glendinning, A. B. 1981 The effective diffusion coefficient detected by dynamic light scattering. J. Chem. Phys. 74 (2), 948–952.Google Scholar
Sarkar, K. & Schowalter, W. R. 2000 Deformation of a two-dimensional viscoelastic drop at non-zero Reynolds number in time-periodic extensional flows. J. Non-Newtonian Fluid Mech. 95 (2–3), 315–342.Google Scholar
Sarkar, K. & Schowalter, W. R. 2001 Deformation of a two-dimensional drop at non-zero Reynolds number in time-periodic extensional flows: numerical simulation. J. Fluid Mech. 436, 177–206.Google Scholar
Sarkar, K. & Singh, R. K. 2013 Spatial ordering due to hydrodynamic interactions between a pair of colliding drops in a confined shear. Phys. Fluids 25 (5), 051702.Google Scholar
Sierou, A. & Brady, J. F. 2004 Shear-induced self-diffusion in non-colloidal suspensions. J. Fluid Mech. 506, 285–314.Google Scholar
Singh, R. K., Li, X. & Sarkar, K. 2013 Lateral migration of a capsule in plane shear near a wall. J. Fluid Mech. 739, 421–443.Google Scholar
Singh, R. K. & Sarkar, K. 2009 Effects of viscosity ratio and three dimensional positioning on hydrodynamic interactions between two viscous drops in a shear flow at finite inertia. Phys. Fluids 21 (10), 103303.Google Scholar
Singh, R. K. & Sarkar, K. 2015 Hydrodynamic interactions between pairs of capsules and drops in a simple shear: Effects of viscosity ratio and heterogeneous collision. Phys. Rev. E 92 (6), 063029.Google Scholar
Srivastava, P., Malipeddi, A. R. & Sarkar, K. 2016 Steady shear rheology of a viscous emulsion in the presence of finite inertia at moderate volume fractions: sign reversal of normal stress differences. J. Fluid Mech. 805, 494–522.Google Scholar
Tan, M. H.-Y., Le, D.-V. & Chiam, K.-H. 2012 Hydrodynamic diffusion of a suspension of elastic capsules in bounded simple shear flow. Soft Matt. 8, 2243–2251.Google Scholar
Taylor, G. I. 1934 The formation of emulsions in definable fields of flow. Proc. R. Soc. Lond. A 146 (A858), 0501–0523.Google Scholar
Towns, J., Cockerill, T., Dahan, M., Foster, I., Gaither, K., Grimshaw, A., Hazlewood, V., Lathrop, S., Lifka, D., Peterson, G. D., Roskies, R., Scott, J. R. & Wilkins-Diehr, N. 2014 XSEDE: accelerating scientific discovery. Comput. Sci. Engng 16 (5), 62–74.Google Scholar
Tryggvason, G., Bunner, B., Esmaeeli, A., Juric, D., Al-Rawahi, N., Tauber, W., Han, J., Nas, S. & Jan, Y.-J. 2001 A front-tracking method for the computations of multiphase flow. J. Comput. Phys. 169 (2), 708–759.Google Scholar
Wang, Y., Mauri, R. & Acrivos, A. 1998 Transverse shear-induced gradient diffusion in a dilute suspension of spheres. J. Fluid Mech. 357, 279.Google Scholar
Zhao, H. & Shaqfeh, E. S. G. 2013 The dynamics of a non-dilute vesicle suspension in a simple shear flow. J. Fluid Mech. 725, 709–731.Google Scholar
Zinchenko, A. Z. & Davis, R. H. 2002 Shear flow of highly concentrated emulsions of deformable drops by numerical simulations. J. Fluid Mech. 455, 21–62.Google Scholar

Malipeddi and Sarkar supplementary movie

A layer of drops diffusing in a shear flow, and the corresponding drop volume fraction as a function of distance along the shear direction evolving with time for Ca=0.05

Download Malipeddi and Sarkar supplementary movie(Video)
Video 4.3 MB