Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-27T01:53:15.695Z Has data issue: false hasContentIssue false
  • English
  • Français

Shear thinning in non-Brownian suspensions explained by variable friction between particles

Published online by Cambridge University Press:  10 December 2018

Laurent Lobry ,
Elisabeth Lemaire ,
Frédéric Blanc ,
Stany Gallier  and
François Peters Open the ORCID record for François Peters [Opens in a new window]
Laurent Lobry
Affiliation:
Institut de Physique de Nice, CNRS UCA, Parc Valrose, 06108 Nice CEDEX 2, France
Elisabeth Lemaire
Affiliation:
Institut de Physique de Nice, CNRS UCA, Parc Valrose, 06108 Nice CEDEX 2, France
Frédéric Blanc
Affiliation:
Institut de Physique de Nice, CNRS UCA, Parc Valrose, 06108 Nice CEDEX 2, France
Stany Gallier
Affiliation:
ArianeGroup, Le Bouchet Research Center, 91710 Vert le Petit, France
François Peters*
Affiliation:
Institut de Physique de Nice, CNRS UCA, Parc Valrose, 06108 Nice CEDEX 2, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose to explain shear-thinning behaviour observed in most concentrated non-Brownian suspensions by variable friction between particles. Considering the low magnitude of the forces experienced by the particles of suspensions under shear flow, it is first argued that rough particles come into solid contact through one or a few asperities. In such a few-asperity elastic–plastic contact, the friction coefficient is expected not to be constant but to decrease with increasing normal load. Simulations based on the force coupling method and including such a load-dependent friction coefficient are performed for various particle volume fractions. 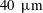The results of the numerical simulations are compared to viscosity measurements carried out on suspensions of polystyrene particles ($40~\unicode[STIX]{x03BC}\text{m}$ in diameter) dispersed in a Newtonian silicon oil. The agreement is shown to be satisfactory. Furthermore, the comparison between the simulations conducted either with a constant or a load-dependent friction coefficient provides a model for the shear-thinning viscosity. In this model the effective friction coefficient 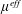$\unicode[STIX]{x1D707}^{eff}$ is specified by the effective normal contact force which is simply proportional to the bulk shear stress. As the shear stress increases, 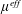$\unicode[STIX]{x1D707}^{eff}$ decreases and the jamming volume fraction increases, leading to the reduction of the viscosity. Finally, using this model, we show that it is possible to evaluate the microscopic friction coefficient for each applied shear stress from the rheometric measurements.

JFM classification

Complex Fluids: Complex Fluids Non-Newtonian Flows: Rheology Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 860 , 10 February 2019 , pp. 682 - 710
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A., Fan, X. & Mauri, R. 1994 On the measurement of the relative viscosity of suspensions. J. Rheol. 38 (5), 1285–1296.Google Scholar
Archard, J. F. 1957 Elastic deformation and the laws of friction. Proc. R. Soc. Lond. A 243 (1233), 190–205.Google Scholar
Biggs, S. & Spinks, G. 1998 Atomic force microscopy investigation of the adhesion between a single polymer sphere and a flat surface. J. Adhes. Sci. Technol. 12 (5), 461–478.Google Scholar
Blanc, F., Peters, F. & Lemaire, E. 2011 Experimental signature of the pair trajectories of rough spheres in the shear-induced microstructure in noncolloidal suspensions. Phys. Rev. Lett. 107 (20), 208302.Google Scholar
Boyer, F., Pouliquen, O. & Guazzelli, É. 2011 Dense suspensions in rotating-rod flows: normal stresses and particle migration. J. Fluid Mech. 686, 5–25.Google Scholar
Brizmer, V., Kligerman, Y. & Etsion, I. 2006a The effect of contact conditions and material properties on the elasticity terminus of a spherical contact. Intl J. Solids Struct. 43 (18), 5736–5749.Google Scholar
Brizmer, V., Kligerman, Y. & Etsion, I. 2007 Elastic–plastic spherical contact under combined normal and tangential loading in full stick. Tribol. Lett. 25 (1), 61–70.Google Scholar
Brizmer, V., Zait, Y., Kligerman, Y. & Etsion, I. 2006b The effect of contact conditions and material properties on elastic-plastic spherical contact. J. Mech. Mater. Struct. 1 (5), 865–879.Google Scholar
Butt, H.-J., Cappella, B. & Kappl, M. 2005 Force measurements with the atomic force microscope: technique, interpretation and applications. Surf. Sci. Rep. 59 (1), 1–152.Google Scholar
Chang, W. R., Etsion, I. & Bogy, D. B. 1987 An elastic–plastic model for the contact of rough surfaces. J. Tribol. 109 (2), 257–263.Google Scholar
Chatté, G., Comtet, J., Niguès, A., Bocquet, L., Siria, A., Ducouret, G., Lequeux, F., Lenoir, N., Ovarlez, G. & Colin, A. 2018 Shear thinning in non-Brownian suspensions. Soft Matt. 14, 879–893.Google Scholar
Chow, A. W., Sinton, S. W., Iwamiya, J. H. & Stephens, T. S. 1994 Shear-induced particle migration in Couette and parallel-plate viscometers: NMR imaging and stress measurements. Phys. Fluids 6 (8), 2561–2576.Google Scholar
Cundall, P. A. & Strack, O. D. 1979 A discrete numerical model for granular assemblies. Geotechnique 29 (1), 47–65.Google Scholar
Dbouk, T.2011 Rheology of concentrated suspensions and shear-induced migration. PhD thesis, Université Nice Sophia Antipolis.Google Scholar
Dbouk, T., Lobry, L. & Lemaire, E. 2013 Normal stresses in concentrated non-Brownian suspensions. J. Fluid Mech. 715, 239–272.Google Scholar
Ducker, W. A., Senden, T. J. & Pashley, R. M. 1992 Measurement of forces in liquids using a force microscope. Langmuir 8 (7), 1831–1836.Google Scholar
Ecke, S. & Butt, H.-J. 2001 Friction between individual microcontacts. J. Colloid Interface Sci. 244 (2), 432–435.Google Scholar
Fernandez, N., Cayer-Barrioz, J., Isa, L. & Spencer, N. D. 2015 Direct, robust technique for the measurement of friction between microspheres. Langmuir 31 (32), 8809–8817.Google Scholar
Fernandez, N., Mani, R., Rinaldi, D., Kadau, D., Mosquet, M., Lombois-Burger, H., Cayer-Barrioz, J., Herrmann, H. J., Spencer, N. D. & Isa, L. 2013 Microscopic mechanism for shear thickening of non-Brownian suspensions. Phys. Rev. Lett. 111 (10), 108301.Google Scholar
Gadala-Maria, F. & Acrivos, A. 1980 Shear-induced structure in a concentrated suspension of solid spheres. J. Rheol. 24 (6), 799–814.Google Scholar
Gallier, S.2014 Simulation numérique de suspensions frictionnelles. Application aux propergols solides. PhD thesis, Université Nice Sophia Antipolis.Google Scholar
Gallier, S., Lemaire, E., Peters, F. & Lobry, L. 2014 Rheology of sheared suspensions of rough frictional particles. J. Fluid Mech. 757, 514–549.Google Scholar
Gallier, S., Peters, F. & Lobry, L. 2018 Simulations of sheared dense non-colloidal suspensions: evaluation of the role of long-range hydrodynamics. Phys. Rev. Fluids 3 (4), 042301.Google Scholar
Garland, S., Gauthier, G., Martin, J. & Morris, J. F. 2013 Normal stress measurements in sheared non-Brownian suspensions. J. Rheol. 57 (1), 71–88.Google Scholar
Greenwood, J. A. & Williamson, J. B. P. 1966 Contact of nominally flat surfaces. Proc. R. Soc. Lond. A 295 (1442), 300–319.Google Scholar
Heim, L. O., Ecke, S., Preuss, M. & Butt, H.-J. 2002 Adhesion forces between individual gold and polystyrene particles. J. Adhes. Sci. Technol. 16 (7), 829–843.Google Scholar
Li, Y. Q., Tao, N. J., Pan, J., Garcia, A. A. & Lindsay, S. M. 1993 Direct measurement of interaction forces between colloidal particles using the scanning force microscope. Langmuir 9 (3), 637–641.Google Scholar
Ling, X., Butt, H.-J. & Kappl, M. 2007 Quantitative measurement of friction between single microspheres by friction force microscopy. Langmuir 23 (16), 8392–8399.Google Scholar
Mari, R., Seto, R., Morris, J. F. & Denn, M. M. 2014 Shear thickening, frictionless and frictional rheologies in non-Brownian suspensions. J. Rheol. 58 (6), 1693–1724.Google Scholar
Merhi, D., Lemaire, E., Bossis, G. & Moukalled, F. 2005 Particle migration in a concentrated suspension flowing between rotating parallel plates: investigation of diffusion flux coefficients. J. Rheol. 49 (6), 1429–1448.Google Scholar
Moon, J. Y., Dai, S., Chang, L., Lee, J. S. & Tanner, R. I. 2015 The effect of sphere roughness on the rheology of concentrated suspensions. J. Non-Newtonian Fluid Mech. 223, 233–239.Google Scholar
Ness, C. & Sun, J. 2015 Flow regime transitions in dense non-Brownian suspensions: rheology, microstructural characterization, and constitutive modeling. Phys. Rev. E 91 (1), 012201.Google Scholar
Ovcharenko, A., Halperin, G. & Etsion, I. 2008 Experimental study of adhesive static friction in a spherical elastic-plastic contact. J. Tribol. 130 (2), 021401.Google Scholar
Pednekar, S., Chun, J. & Morris, J. F. 2018 Bidisperse and polydisperse suspension rheology at large solid fraction. J. Rheol. 62 (2), 513–526.Google Scholar
Peters, F., Ghigliotti, G., Gallier, S., Blanc, F., Lemaire, E. & Lobry, L. 2016 Rheology of non-Brownian suspensions of rough frictional particles under shear reversal: a numerical study. J. Rheol. 60 (4), 715–732.Google Scholar
Pham, P., Metzger, B. & Butler, J. E. 2015 Particle dispersion in sheared suspensions: crucial role of solid-solid contacts. Phys. Fluids 27 (5), 051701.Google Scholar
Reitsma, M., Craig, V. & Biggs, S. 2000 Elasto-plastic and visco-elastic deformations of a polymer sphere measured using colloid probe and scanning electron microscopy. Intl J. Adhes. Adhes. 20 (6), 445–448.Google Scholar
Schaefer, D. M., Carpenter, M., Gady, B., Reifenberger, R., Demejo, L. P. & Rimai, D. S. 1995 Surface roughness and its influence on particle adhesion using atomic force techniques. J. Adhes. Sci. Technol. 9 (8), 1049–1062.Google Scholar
Seto, R., Giusteri, G. G. & Martiniello, A. 2017 Microstructure and thickening of dense suspensions under extensional and shear flows. J. Fluid Mech. 825, R3.Google Scholar
Seto, R., Mari, R., Morris, J. F. & Denn, M. M. 2013 Discontinuous shear thickening of frictional hard-sphere suspensions. Phys. Rev. Lett. 111 (21), 218301.Google Scholar
Shäfer, J., Dippel, S. & Wolf, D. 1996 Force schemes in simulations of granular materials. J. Phys. I France 6, 5–20.Google Scholar
Sierou, A. & Brady, J. F. 2002 Rheology and microstructure in concentrated noncolloidal suspensions. J. Rheol. 46 (5), 1031–1056.Google Scholar
Silbert, L. E. 2010 Jamming of frictional spheres and random loose packing. Soft Matt. 6 (13), 2918–2924.Google Scholar
Singh, A., Mari, R., Denn, M. M. & Morris, J. F. 2018 A constitutive model for simple shear of dense frictional suspensions. J. Rheol. 62 (2), 457–468.Google Scholar
Tabor, D. 1981 Friction – the present state of our understanding. J. Lubr. Technol. 103 (2), 169–179.Google Scholar
Tanner, R. I. & Dai, S. 2016 Particle roughness and rheology in noncolloidal suspensions. J. Rheol. 60 (4), 809–818.Google Scholar
Tanner, R. I., Ness, C., Mahmud, A., Dai, S. & Moon, J. 2018 A bootstrap mechanism for non-colloidal suspension viscosity. Rheol. Acta 57 (10), 635–643.Google Scholar
Vazquez-Quesada, A., Mahmud, A., Dai, S., Ellero, M. & Tanner, R. I. 2017 Investigating the causes of shear-thinning in non-colloidal suspensions: experiments and simulations. J. Non-Newtonian Fluid Mech 248, 1–7.Google Scholar
Vázquez-Quesada, A., Tanner, R. I. & Ellero, M. 2016 Shear thinning of noncolloidal suspensions. Phys. Rev. Lett. 117 (10), 108001.Google Scholar
Yeo, K. & Maxey, M. R. 2010a Dynamics of concentrated suspensions of non-colloidal particles in Couette flow. J. Fluid Mech. 649, 205–231.Google Scholar
Yeo, K. & Maxey, M. R. 2010b Simulation of concentrated suspensions using the force-coupling method. J. Comput. Phys. 229 (6), 2401–2421.Google Scholar
Zarraga, I. E., Hill, D. A. & Leighton, D. T. Jr 2000 The characterization of the total stress of concentrated suspensions of noncolloidal spheres in Newtonian fluids. J. Rheol. 44 (2), 185–220.Google Scholar
Zou, Y., Jayasuriya, S., Manke, C. W. & Mao, G. 2015 Influence of nanoscale surface roughness on colloidal force measurements. Langmuir 31 (38), 10341–10350.Google Scholar