Published online by Cambridge University Press: 21 February 2020
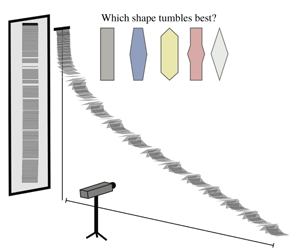
Tumbling wings are one of Nature’s many tricks to enhance the dispersal efficiency of flying seedpods. However, the interplay between the seedpod morphology and its dispersal range is not well understood. Here, we investigate the question of how planform geometry affects two-dimensional tumbling flight by designing wings of various planform and length-to-width ratios. Through a combination of experiments and modelling, we compare the wings’ flight characteristics, specifically the rotation rate and descent angle, both of which are key parameters in the wing’s ability to drift away from its initial location. Starting from the quasi-steady flight model proposed by Wang et al. (J. Fluid Mech., vol. 733, 2013, pp. 650–679), we derive theoretical predictions of the performance of wings of arbitrary planform. Upon further simplifications, we arrive at a performance index based purely on wing geometry and we use it to obtain theoretically optimal wing shapes. These optimal predictions are then tested experimentally. We conclude by discussing the advantages and limitations of the theoretical approach and its utility in informing the design of aerodynamically efficient tumbling wings.