Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-29T19:44:14.910Z Has data issue: false hasContentIssue false
  • English
  • Français

Shallow, gravity-driven flow in a poro-elastic layer

Published online by Cambridge University Press:  05 August 2015

Duncan R. Hewitt ,
Jerome A. Neufeld  and
Neil J. Balmforth
Duncan R. Hewitt*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK Department of Mathematics, University of British Columbia, Vancouver, BC, CanadaV6T 1Z2
Jerome A. Neufeld
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge CB3 0WA, UK Department of Earth Science, University of Cambridge, Cambridge CB3 0EZ, UK BP Institute, University of Cambridge, Cambridge CB3 0EZ, UK
Neil J. Balmforth
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC, CanadaV6T 1Z2
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

By combining Biot’s theory of poro-elasticity with standard shallow-layer scalings, a theoretical model is developed to describe axisymmetric gravity-driven flow through a shallow deformable porous medium. Motivated in part by observations of surface uplift around $\text{CO}_{2}$ sequestration sites, the model is used to explore the injection of a dense fluid into a horizontal, deformable porous layer that is initially saturated with another, less dense, fluid. The layer lies between a rigid base and a flexible overburden, both of which are impermeable. As the injected fluid spreads under gravity, the matrix deforms and the overburden lifts up. The coupled model predicts the location of the injected fluid as it spreads and the resulting uplift of the overburden due to deformation of the solid matrix. In general, the uplift spreads diffusively far ahead of the injected fluid. If fluid is injected with a constant flux and the medium is unbounded, both the uplift and the injected fluid spread in a self-similar fashion with the same similarity variable 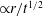$\propto r/t^{1/2}$. The asymptotic form of this spreading is established. Results from a series of laboratory experiments, using polyacrylamide hydrogel particles to create a soft poro-elastic material, are compared qualitatively with the predictions of the model.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 778 , 10 September 2015 , pp. 335 - 360
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barabadi, B., Nathan, R., Jen, K. & Wu, Q. 2009 On the characterization of lifting forces during the rapid compaction of deformable porous media. Trans. ASME J. Heat Transfer 131 (10), 101006.Google Scholar
Barry, S. I. & Holmes, M. 2001 Asymptotic behaviour of thin poroelastic layers. IMA J. Appl. Maths 66, 175–194.Google Scholar
Barry, S. I., Mercer, G. N. & Zoppou, C. 1997 Deformation and fluid flow due to a source in a poro-elastic layer. Appl. Math. Model. 21 (11), 681–689.Google Scholar
Bear, J. 1988 Dynamics of Fluids in Porous Media. Dover.Google Scholar
Bear, J. & Corapcioglu, M. Y. 1981a A mathematical model for consolidation in a thermoelastic aquifer due to hot water injection or pumping. Water Resour. Res. 17 (3), 723–736.Google Scholar
Bear, J. & Corapcioglu, M. Y. 1981b Mathematical model for regional land subsidence due to pumping: 1. Integrated aquifer subsidence equations based on vertical displacement only. Water Resour. Res. 17 (4), 937–946.Google Scholar
Bear, J. & Corapcioglu, M. Y. 1981c Mathematical model for regional land subsidence due to pumping: 2. Integrated aquifer subsidence equations for vertical and horizontal displacements. Water Resour. Res. 17 (4), 947–958.CrossRefGoogle Scholar
Bissell, R. C., Vasco, D. W., Atbi, M., Hamdani, M., Okwelegbe, M. & Goldwater, M. H. 2011 A full field simulation of the In Salah gas production and $\text{CO}_{2}$ storage project using a coupled geo-mechanical and thermal fluid flow simulator. Energy Proc. 4, 3290–3297.Google Scholar
Boait, F. C., White, N. J., Bickle, M. J., Chadwick, R. A., Neufeld, J. A. & Huppert, H. E. 2012 Spatial and temporal evolution of injected $\text{CO}_{2}$ at the Sleipner Field, North Sea. J. Geophys. Res. 117, 2156–2202.Google Scholar
Charras, G. T., Mitchison, T. J. & Mahadevan, L. 2009 Animal cell hydraulics. J. Cell Sci. 122 (18), 3233–3241.Google Scholar
Coussy, O. 2004 Poromechanics. Wiley.Google Scholar
Detournay, E. & Cheng, A. H.-D. 1993 Fundamentals of poroelasticity. In Comprehensive Rock Engineering: Principles, Practice and Projects, Vol. II, Analysis and Design Method, chap. 5., Pergamon.Google Scholar
Eisenberg, S. R. & Grodzinsky, A. J. 1987 The kinetics of chemically induced nonequilibrium swelling of cartilage and corneal stroma. J. Biomed. Engng 109, 79–89.Google ScholarPubMed
Gibson, R. E., Schiffman, R. L. & Pu, S. L. 1970 Plane strain and axially symmetric consolidation of a clay layer on a smooth impervious base. Q. J. Mech. Appl. Maths 23 (4), 505–520.Google Scholar
Huppert, H. E. & Neufeld, J. A. 2014 The fluid mechanics of carbon dioxide sequestration. Annu. Rev. Fluid Mech. 46, 255–272.Google Scholar
Huppert, H. E. & Woods, A. 1995 Gravity-driven flows in porous layers. J. Fluid Mech. 292, 55–69.CrossRefGoogle Scholar
Jensen, O. E., Glucksberg, M. R., Sachs, J. R. & Grotberg, J. B. 1994 Weakly nonlinear deformation of a thin poroelastic layer with a free surface. J. Appl. Mech. 61 (3), 729–731.Google Scholar
Lanir, Y., Sauob, S. & Maretsky, P. 1990 Nonlinear finite deformation response of open cell polyurethane sponge to fluid filtration. J. Appl. Mech. 57, 449–454.Google Scholar
Lister, J. R., Peng, G. & Neufeld, J. A. 2013 Viscous control of peeling an elastic sheet by bending and pulling. Phys. Rev. Lett. 111, 154501.Google Scholar
Lyle, S., Huppert, H. E., Hallworth, M. A., Bickle, M. & Chadwick, A. 2005 Axisymmeteric gravity currents in a porous medium. J. Fluid Mech. 543, 293–302.CrossRefGoogle Scholar
MacMinn, C. W., Dufresne, E. R. & Wettlaufer, J. S. 2015 Fluid-driven deformation of a soft granular material. Phys. Rev. X 5, 011020.Google Scholar
Mak, A. F., Lai, W. M. & Mow, V. C. 1987 Biphasic indentation of articular cartilage I. Theoretical analysis. J. Biomech. 20 (7), 703–714.Google Scholar
Moeendarbary, E., Valon, L., Fritzsche, M., Harris, A. R., Moulding, D. A., Thrasher, A. J., Stride, E., Mahadevan, L. & Charras, G. T. 2013 The cytoplasm of living cells behaves as a poroelastic material. Nat. Mater. 12 (3), 253–261.Google Scholar
Mow, V. C., Gibbs, M. C., Lai, W. M., Zhu, W. B. & Athanasiou, K. A. 1989 Biphasic indentation of articular cartilage II. A numerical algorithm and an experimental study. J. Biomech. 22 (8), 853–861.Google Scholar
Mow, V. C., Holmes, M. H. & Lai, W. M. 1984 Fluid transport and mechanical properties of articular cartilage: a review. J. Biomech. 17, 377–394.Google Scholar
Nordbotten, J. M. & Celia, M. A. 2006 Similarity solutions for fluid injection into confined aquifers. J. Fluid Mech. 561, 307–327.Google Scholar
Onuma, T. & Ohkawa, S. 2009 Detection of surface deformation related with $\text{CO}_{2}$ injection by DInSAR at In Salah, Algeria. Energy Proc. 1, 2177–2184.Google Scholar
Parker, K. H., Mehta, R. V. & Caro, C. G. 1987 Steady flow in porous, elastically deformable materials. J. Appl. Mech. 54, 794–799.Google Scholar
Pegler, S. S., Huppert, H. E. & Neufeld, J. A. 2014 Fluid injection into a confined porous layer. J. Fluid Mech. 745, 592–620.Google Scholar
Phillips, O. M. 2009 Geological Fluids Dynamics. Cambridge University Press.Google Scholar
Ringrose, P., Atbi, M., Mason, D., Espinassous, M., Myhrer, Ø., Iding, M., Mathieson, A. & Wright, I. 2009 Plume development around well KB-502 at the In Salah $\text{CO}_{2}$ storage site. First Break 27 (1), 85–89.CrossRefGoogle Scholar
Ringrose, P. S., Mathieson, A. S., Wright, I. W., Selama, F., Hansen, O., Bissell, R., Saoula, N. & Midgley, J. 2013 The In Salah $\text{CO}_{2}$ storage project: lessons learned and knowledge transfer. Energy Proc. 37, 6226–6236.Google Scholar
Rucci, A., Vasco, D. W. & Novali, F. 2013 Monitoring the geologic storage of carbon dioxide using multicomponent sar interferometry. Geophys. J. Intl 193, 197–208.Google Scholar
Rutqvist, J. 2012 The geomechanics of $\text{CO}_{2}$ storage in deep sedimentary formations. Geotech. Geol. Engng 30, 525–551.Google Scholar
Rutqvist, J., Vasco, D. W. & Myer, L. 2010 Coupled reservoir-geomechanical analysis of $\text{CO}_{2}$ injection and ground deformations at In Salah, Algeria. Intl J. Greenh. Gas Control 4, 225–230.Google Scholar
Sachs, J. R., Glucksberg, M. R., Jensen, O. E. & Grotberg, J. B. 1994 Linear flow and deformation in a poroelastic disk with a free surface. J. Appl. Mech. 61 (3), 726–728.Google Scholar
Simon, B. R., Liable, J. P., Pflaster, D., Yuan, Y. & Krag, M. H. 1996 A poroelastic finite element formulation including transport and swelling in soft tissue structure. Trans. ASME J. Biomech. Engng 118, 1–9.CrossRefGoogle Scholar
Wang, H. F. 2000 Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology. Princeton University Press.Google Scholar
Zhang, W. 2013 Density-driven enhanced dissolution of injected $\text{CO}_{2}$ during long-term $\text{CO}_{2}$ storage. J. Earth Syst. Sci. 122, 1387–1397.Google Scholar