Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-23T11:59:16.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Sensitivity and open-loop control of stochastic response in a noise amplifier flow: the backward-facing step

Published online by Cambridge University Press:  03 December 2014

E. Boujo  and
F. Gallaire
E. Boujo*
Affiliation:
LFMI, École Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland
F. Gallaire
Affiliation:
LFMI, École Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The two-dimensional backward-facing step flow is a canonical example of noise amplifier flow: global linear stability analysis predicts that it is stable, but perturbations can undergo large amplification in space and time as a result of non-normal effects. This amplification potential is best captured by optimal transient growth analysis, optimal harmonic forcing, or the response to sustained noise. With a view to reducing disturbance amplification in these globally stable open flows, a variational technique is proposed to evaluate the sensitivity of stochastic amplification to steady control. Existing sensitivity methods are extended in two ways to achieve a realistic representation of incoming noise: (i) perturbations are time-stochastic rather than time-harmonic, (ii) perturbations are localised at the inlet rather than distributed in space. This allows the identification of regions where small-amplitude control is the most effective, without actually computing any controlled flows. In particular, passive control by means of a small cylinder and active control by means of wall blowing/suction are analysed for Reynolds number $\mathit{Re}=500$ and step-to-outlet expansion ratio 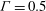${\it\Gamma}=0.5$. Sensitivity maps for noise amplification appear largely similar to sensitivity maps for optimal harmonic amplification at the most amplified frequency. This is observed at other values of 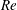$\mathit{Re}$ and 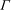${\it\Gamma}$ too, and suggests that the design of steady control in this noise amplifier flow can be simplified by focusing on the most dangerous perturbation at the most dangerous frequency.

JFM classification

Flow Control: Flow Control Flow Control: Instability control Wakes/Jets: Separated flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 762 , 10 January 2015 , pp. 361 - 392
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Åkervik, E., Ehrenstein, U., Gallaire, F. & Henningson, D. S. 2008 Global two-dimensional stability measures of the flat plate boundary-layer flow. Eur. J. Mech. (B/Fluids) 27 (5), 501–513.CrossRefGoogle Scholar
Alizard, F., Cherubini, S. & Robinet, J.-C. 2009 Sensitivity and optimal forcing response in separated boundary layer flows. Phys. Fluids 21 (6), 064108.CrossRefGoogle Scholar
Armaly, B. F., Durst, F., Pereira, J. C. F. & Schönung, B. 1983 Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech. 127, 473–496.CrossRefGoogle Scholar
Barkley, D., Gomes, M. G. M. & Henderson, R. D. 2002 Three-dimensional instability in flow over a backward-facing step. J. Fluid Mech. 473, 167–190.CrossRefGoogle Scholar
Beaudoin, J.-F., Cadot, O., Aider, J.-L. & Wesfreid, J. E. 2004 Three-dimensional stationary flow over a backward-facing step. Eur. J. Mech. (B/Fluids) 23 (1), 147–155.CrossRefGoogle Scholar
Beaudoin, J.-F., Cadot, O., Aider, J.-L. & Wesfreid, J.-E. 2006 Drag reduction of a bluff body using adaptive control methods. Phys. Fluids 18 (8), 085107.CrossRefGoogle Scholar
Blackburn, H. M., Barkley, D. & Sherwin, S. J. 2008 Convective instability and transient growth in flow over a backward-facing step. J. Fluid Mech. 603, 271–304.CrossRefGoogle Scholar
Bottaro, A., Corbett, P. & Luchini, P. 2003 The effect of base flow variation on flow stability. J. Fluid Mech. 476, 293–302.CrossRefGoogle Scholar
Boujo, E., Ehrenstein, U. & Gallaire, F. 2013 Open-loop control of noise amplification in a separated boundary layer flow. Phys. Fluids 25 (12), 124106.CrossRefGoogle Scholar
Boujo, E. & Gallaire, F. 2014a Controlled reattachment in separated flows: a variational approach to recirculation length reduction. J. Fluid Mech. 742, 618–635.CrossRefGoogle Scholar
Boujo, E. & Gallaire, F. 2014b Manipulating flow separation: sensitivity of stagnation points, separatrix angles and recirculation area to steady actuation. Proc. R. Soc. Lond. A 470 (2170), 20140365.Google ScholarPubMed
Brandt, L., Sipp, D., Pralits, J. O. & Marquet, O. 2011 Effect of base-flow variation in noise amplifiers: the flat-plate boundary layer. J. Fluid Mech. 687, 503–528.CrossRefGoogle Scholar
Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4 (8), 1637–1650.CrossRefGoogle Scholar
Cadot, O., Thiria, B. & Beaudoin, J.-F. 2009 Passive drag control of a turbulent wake by local disturbances. In IUTAM Symposium on Unsteady Separated Flows and their Control (ed. Braza, M. & Hourigan, K.), IUTAM Bookseries, vol. 14, pp. 529–537. Springer.CrossRefGoogle Scholar
Cantwell, C. D., Barkley, D. & Blackburn, H. M. 2010 Transient growth analysis of flow through a sudden expansion in a circular pipe. Phys. Fluids 22 (3), 034101.CrossRefGoogle Scholar
Corbett, P. & Bottaro, A. 2000 Optimal perturbations for boundary layers subject to stream-wise pressure gradient. Phys. Fluids 12 (1), 120–130.CrossRefGoogle Scholar
Cossu, C. 2014 An introduction to optimal control, lecture notes from the FLOW-NORDITA summer school on advanced instability methods for complex flows, Stockholm, Sweden, 2013. Appl. Mech. Rev. 66 (2), 024801.Google Scholar
Dalton, C., Xu, Y. & Owen, J. C. 2001 The suppression of lift on a circular cylinder due to vortex shedding at moderate Reynolds numbers. J. Fluids Struct. 15, 617–628.CrossRefGoogle Scholar
Dergham, G., Sipp, D. & Robinet, J.-Ch. 2013 Stochastic dynamics and model reduction of amplifier flows: the backward facing step flow. J. Fluid Mech. 719, 406–430.CrossRefGoogle Scholar
Fani, A., Camarri, S. & Salvetti, M. V. 2012 Stability analysis and control of the flow in a symmetric channel with a sudden expansion. Phys. Fluids 24 (8), 084102.CrossRefGoogle Scholar
Farrell, B. F. & Ioannou, P. J. 1996 Generalized stability theory. Part I: autonomous operators. J. Atmos. Sci. 53, 2025–2040.2.0.CO;2>CrossRefGoogle Scholar
Garnaud, X., Lesshafft, L., Schmid, P. J. & Huerre, P. 2013 The preferred mode of incompressible jets: linear frequency response analysis. J. Fluid Mech. 716, 189–202.CrossRefGoogle Scholar
Gaster, M. 1962 A note on the relation between temporally-increasing and spatially-increasing disturbances in hydrodynamic stability. J. Fluid Mech. 14, 222–224.CrossRefGoogle Scholar
Henning, L. & King, R. 2007 Robust multivariable closed-loop control of a turbulent backward-facing step flow. J. Aircraft 44 (1), 201–208.CrossRefGoogle Scholar
Hervé, A., Sipp, D., Schmid, P. J. & Samuelides, M. 2012 A physics-based approach to flow control using system identification. J. Fluid Mech. 702, 26–58.CrossRefGoogle Scholar
Hill, D. C.1992 A theoretical approach for analyzing the restabilization of wakes. AIAA Paper 92-0067.CrossRefGoogle Scholar
Igarashi, T. 1997 Drag reduction of a square prism by flow control using a small rod. J. Wind Engng Ind. Aerodyn. 69–71, 141–153; Proceedings of the 3rd International Colloquium on Bluff Body Aerodynamics and Applications.CrossRefGoogle Scholar
Kaiktsis, L., Karniadakis, G. E. & Orszag, S. A. 1996 Unsteadiness and convective instabilities in two-dimensional flow over a backward-facing step. J. Fluid Mech. 321, 157–187.CrossRefGoogle Scholar
Lanzerstorfer, D. & Kuhlmann, H. C. 2012 Global stability of the two-dimensional flow over a backward-facing step. J. Fluid Mech. 693, 1–27.CrossRefGoogle Scholar
Marquet, O. & Sipp, D. 2010 Global sustained perturbations in a backward-facing step flow. In Seventh IUTAM Symposium on Laminar-Turbulent Transition (ed. Schlatter, P. & Henningson, D. S.), IUTAM Bookseries, vol. 18, pp. 525–528. Springer.CrossRefGoogle Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
Marquet, O., Sipp, D. & Lesshafft, L.2010 Global stability analysis of open shear flows without global modes. Unpublished.Google Scholar
Meliga, P., Sipp, D. & Chomaz, J.-M. 2010 Open-loop control of compressible afterbody flows using adjoint methods. Phys. Fluids 22 (5), 054109.CrossRefGoogle Scholar
Mittal, S. & Raghuvanshi, A. 2001 Control of vortex shedding behind circular cylinder for flows at low Reynolds numbers. Intl J. Numer. Meth. Fluids 35 (4), 421–447.3.0.CO;2-M>CrossRefGoogle Scholar
Oseen, C. W. 1910 Über die Stokes’sche Formel, und über eine verwandte Aufgabe in der Hydrodynamik. Ark. Mat. Astron. Fys. vi (29).Google Scholar
Parezanović, V. & Cadot, O. 2009 The impact of a local perturbation on global properties of a turbulent wake. Phys. Fluids 21 (7), 071701.CrossRefGoogle Scholar
Parezanović, V. & Cadot, O. 2012 Experimental sensitivity analysis of the global properties of a two-dimensional turbulent wake. J. Fluid Mech. 693, 115–149.CrossRefGoogle Scholar
Pastoor, M., King, R., Noack, B. R. & Tadmor, G. 2005 Observers and feedback control for shear layer vortices. In 44th IEEE Conference on Decision and Control, 2005 and 2005 European Control Conference. CDC-ECC’05, pp. 506–511. IEEE.Google Scholar
Pralits, J. O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.CrossRefGoogle Scholar
Proudman, I. & Pearson, J. R. A. 1957 Expansions at small Reynolds numbers for the flow past a sphere and a circular cylinder. J. Fluid Mech. 2, 237–262.CrossRefGoogle Scholar
Reynolds, O. 1883 An experimental investigation of the circumstances which determine whether the motion of water shall be direct or sinuous, and of the law of resistance in parallel channels. Phil. Trans. R. Soc. Lond. 174, 935–982.Google Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
Sinha, S. N., Gupta, A. K. & Oberai, M. 1981 Laminar separating flow over backsteps and cavities. I – backsteps. AIAA J. 19, 1527–1530.CrossRefGoogle Scholar
Sipp, D. & Marquet, O. 2013 Characterization of noise amplifiers with global singular modes: the case of the leading-edge flat-plate boundary layer. Theor. Comput. Fluid Dyn. 27 (5), 617–635.CrossRefGoogle Scholar
Strykowski, P. J. & Sreenivasan, K. R. 1990 On the formation and suppression of vortex ‘shedding’ at low Reynolds numbers. J. Fluid Mech. 218, 71–107.CrossRefGoogle Scholar
Tomotika, S. & Aoi, T. 1951 An expansion formula for the drag on a circular cylinder moving through a viscous fluid at small Reynolds numbers. Q. J. Mech. Appl. Maths 4 (4), 401–406.CrossRefGoogle Scholar
Trefethen, L. N., Trefethen, A. E., Reddy, S. C. & Driscoll, T. A. 1993 Hydrodynamic stability without eigenvalues. Science 261 (5121), 578–584.CrossRefGoogle ScholarPubMed
Tritton, D. J. 1959 Experiments on the flow past a circular cylinder at low Reynolds numbers. J. Fluid Mech. 6, 547–567.CrossRefGoogle Scholar
Zhou, K., Doyle, J. C. & Glover, K. 1996 Robust and Optimal Control. Prentice Hall.Google Scholar