Article contents
Self-similar dynamics of two-phase flows injected into a confined porous layer
Published online by Cambridge University Press: 02 September 2019
Abstract
We study the dynamics of two-phase flows injected into a confined porous layer. A model is derived to describe the evolution of the fluid–fluid interface, where the effective saturation of the injected fluid is zero. The flow is driven by pressure gradients due to injection, the buoyancy due to density contrasts and the interfacial tension between the injected and ambient fluids. The saturation field is then computed after the interface evolution is obtained. The results demonstrate that the flow behaviour evolves from early-time unconfined to late-time confined behaviours. In particular, at early times, the influence of capillary forces drives fluid flow and produces a new self-similar spreading behaviour in the unconfined limit that is distinct from the gravity current solution. At late times, we obtain two new similarity solutions, a modified shock solution and a compound wave solution, in addition to the rarefaction and shock solutions in the sharp-interface limit. A schematic regime diagram is also provided, which summarises all possible similarity solutions and the time transitions between them for the partially saturating flows resulting from fluid injection into a confined porous layer. Three dimensionless control parameters are identified and their influence on the fluid flow is also discussed, including the viscosity ratio, the pore-size distribution and the relative contributions of capillary and buoyancy forces. To underline the relevance of our results, we also briefly describe the implications of the two-phase flow model to the geological storage of 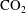 $\text{CO}_{2}$, using representative geological parameters from the Sleipner and In Salah sites.
$\text{CO}_{2}$, using representative geological parameters from the Sleipner and In Salah sites.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 10
- Cited by


