Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-24T12:35:18.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-organized criticality of turbulence in strongly stratified mixing layers

Published online by Cambridge University Press:  02 October 2018

Hesam Salehipour Open the ORCID record for Hesam Salehipour [Opens in a new window] ,
W. R. Peltier  and
C. P. Caulfield Open the ORCID record for C. P. Caulfield [Opens in a new window]
Hesam Salehipour*
Affiliation:
Department of Physics, University of Toronto, Toronto, ON M5S 1A7, Canada Autodesk Research, MaRS Discovery District, 661 University Ave, Toronto, ON M5G 1M1, Canada
W. R. Peltier
Affiliation:
Department of Physics, University of Toronto, Toronto, ON M5S 1A7, Canada
C. P. Caulfield
Affiliation:
BP Institute, University of Cambridge, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by the importance of stratified shear flows in geophysical and environmental circumstances, we characterize their energetics, mixing and spectral behaviour through a series of direct numerical simulations of turbulence generated by Holmboe wave instability (HWI) under various initial conditions. We focus on circumstances where the stratification is sufficiently ‘strong’ so that HWI is the dominant primary instability of the flow. Our numerical findings demonstrate the emergence of self-organized criticality (SOC) that is manifest as an adjustment of an appropriately defined gradient Richardson number, $Ri_{g}$, associated with the horizontally averaged mean flow, in such a way that it is continuously attracted towards a critical value of 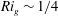$Ri_{g}\sim 1/4$. This self-organization occurs through a continuously reinforced localization of the ‘scouring’ motions (i.e. ‘avalanches’) that are characteristic of the turbulence induced by the breakdown of Holmboe wave instabilities and are developed on the upper and lower flanks of the sharply localized density interface, embedded within a much more diffuse shear layer. These localized ‘avalanches’ are also found to exhibit the expected scale-invariant characteristics. From an energetics perspective, the emergence of SOC is expressed in the form of a long-lived turbulent flow that remains in a ‘quasi-equilibrium’ state for an extended period of time. Most importantly, the irreversible mixing that results from such self-organized behaviour appears to be characterized generically by a universal cumulative turbulent flux coefficient of 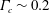$\unicode[STIX]{x1D6E4}_{c}\sim 0.2$ only for turbulent flows engendered by Holmboe wave instability. The existence of this self-organized critical state corroborates the original physical arguments associated with self-regulation of stratified turbulent flows as involving a ‘kind of equilibrium’ as described by Turner (1973, Buoyancy Effects in Fluids, Cambridge University Press).

JFM classification

Turbulent Flows: Stratified turbulence Mixing: Turbulent mixing Turbulent Flows: Turbulent transition
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 856 , 10 December 2018 , pp. 228 - 256
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aschwanden, M. J. et al. 2016 25 years of self-organized criticality: solar and astrophysics. Space Sci. Rev. 198 (1–4), 47–166.Google Scholar
Baines, P. G. & Mitsudera, H. 1994 On the mechanism of shear flow instabilities. J. Fluid Mech. 276, 327–342.Google Scholar
Bak, P., Tang, C. & Wiesenfeld, K. 1987 Self-organized criticality: an explanation of the 1/f noise. Phys. Rev. Lett. 59 (4), 381–384.Google Scholar
Butler, S. & Peltier, W. R. 1997 Internal thermal boundary layer stability in phase transition modulated convection. J. Geophys. Res. 102 (B2), 2731–2749.Google Scholar
Caulfield, C. P. 1994 Multiple linear instability of a layered stratified shear flow. J. Fluid Mech. 258, 155–285.Google Scholar
Caulfield, C. P. & Peltier, W. R. 2000 The anatomy of the mixing transition in homogeneous and stratified free shear layers. J. Fluid Mech. 413, 1–47.Google Scholar
Ellison, T. H. 1957 Turbulent transport of heat and momentum from an infinite rough plane. J. Fluid Mech. 2 (05), 456–466.Google Scholar
Fischer, P. F. 1997 An overlapping Schwarz method for spectral element solution of the incompressible Navier–Stokes equations. J. Comput. Phys. 133 (1), 84–101.Google Scholar
Gregg, M. C., D’Asaro, E. A., Riley, J. J. & Kunze, E. 2018 Mixing efficiency in the ocean. Annu. Rev. Marine Sci. 10, 443–473.Google Scholar
Guha, A. & Lawrence, G. A. 2014 A wave interaction approach to studying non-modal homogeneous and stratified shear instabilities. J. Fluid Mech. 755, 336–364.Google Scholar
Hogg, A. McC. & Ivey, G. N. 2003 The Kelvin–Helmholtz to Holmboe instability transition in stratified exchange flows. J. Fluid Mech. 477, 339–362.Google Scholar
Holleman, R. C., Geyer, W. R. & Ralston, D. K. 2016 Stratified turbulence and mixing efficiency in a salt wedge estuary. J. Phys. Oceanogr. 46 (6), 1769–1783.Google Scholar
Holmboe, J. 1962 On the behaviour of symmetric waves in stratified shear layers. Geofys. Publ. Oslo 24, 67–113.Google Scholar
Holt, S. E., Koseff, J. R. & Ferziger, J. H. 1992 A numerical study of the evolution and structure of homogeneous stably stratified sheared turbulence. J. Fluid Mech. 237, 499–539.Google Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10, 509–512.Google Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40 (1), 169–184.Google Scholar
Lawrence, G., Pieters, R., Zaremba, L., Tedford, T., Gu, L., Greco, S. & Hamblin, P. 2004 Summer exchange between Hamilton Harbour and Lake Ontario. Deep-Sea Res. II 51 (4–5), 475–487.Google Scholar
Lawrence, G. A., Browand, F. K. & Redekopp, L. G. 1991 The stability of a sheared density interface. Phys. Fluids A 3 (10), 2360–2370.Google Scholar
Lefauve, A., Partridge, J. L., Zhou, Q., Dalziel, S. B., Caulfield, C. P. & Linden, P. F. 2018 The structure and origin of confined Holmboe waves. J. Fluid Mech. 848, 508–544.Google Scholar
Lilly, D. K. 1983 Stratified turbulence and the mesoscale variability of the atmosphere. J. Atmos. Sci. 40 (3), 749–761.Google Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.Google Scholar
Linden, P. F. 1979 Mixing in stratified fluids. Geophys. Astrophys. Fluid Dyn. 13, 3–23.Google Scholar
Macagno, E. O. & Rouse, H. 1961 Interfacial mixing in stratified flow. J. Engng Mechanics Division. Proc. Am. Soc. Civil Engineers 87 (EM5), 55–81.Google Scholar
Mashayek, A., Caulfield, C. P. & Peltier, W. R. 2013 Time-dependent, non-monotonic mixing in stratified turbulent shear flows: implications for oceanographic estimates of buoyancy flux. J. Fluid Mech. 736, 570–593.Google Scholar
Mashayek, A. & Peltier, W. R. 2013 Shear induced mixing in geophysical flows: does the route to turbulence matter to its efficiency? J. Fluid Mech. 725, 216–261.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10, 496–508.Google Scholar
Osborn, T. R. 1980 Estimates of the local rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10, 83–89.Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35, 135–167.Google Scholar
Pruessner, G. 2012 Self-Organised Criticality: Theory, Models and Characterisation. Cambridge University Press.Google Scholar
Rohr, J. J., Itsweire, E. C., Helland, K. N. & Van Atta, C. W. 1988 Growth and decay of turbulence in a stably stratified shear flow. J. Fluid Mech. 195, 77–111.Google Scholar
Salehipour, H., Caulfield, C. P. & Peltier, W. R. 2016 Turbulent mixing due to the Holmboe wave instability at high Reynolds number. J. Fluid Mech. 803, 591–621.Google Scholar
Salehipour, H. & Peltier, W. R. 2015 Diapycnal diffusivity, turbulent Prandtl number and mixing efficiency in Boussinesq stratified turbulence. J. Fluid Mech. 775, 464–500.Google Scholar
Salehipour, H., Peltier, W. R. & Mashayek, A. 2015 Turbulent diapycnal mixing in stratified shear flows: the influence of Prandtl number on mixing efficiency and transition at high Reynolds number. J. Fluid Mech. 773, 178–223.Google Scholar
Shih, L. H., Koseff, J. R., Ferziger, J. H. & Rehmann, C. R. 2000 Scaling and parameterization of stratified homogeneous turbulent shear flow. J. Fluid Mech. 412, 1–20.Google Scholar
Smyth, W. D., Carpenter, J. R. & Lawrence, G. A. 2007 Mixing in symmetric Holmboe waves. J. Phys. Oceanogr. 37, 1566–1583.Google Scholar
Smyth, W. D. & Moum, J. N. 2013 Marginal instability and deep cycle turbulence in the eastern equatorial Pacific Ocean. Geophys. Res. Lett. 40 (23), 6181–6185.Google Scholar
Smyth, W. D., Moum, J. N., Li, L. & Thorpe, S. A. 2013 Diurnal shear instability, the descent of the surface shear layer, and the deep cycle of equatorial turbulence. J. Phys. Oceanogr. 43 (11), 2432–2455.Google Scholar
Smyth, W. D. & Peltier, W. R. 1989 The transition between Kelvin–Helmholtz and Holmboe instability: an investigation of the overreflection hypothesis. J. Atmos. Sci. 46 (24), 3698–3720.Google Scholar
Smyth, W. D. & Winters, K. B. 2003 Turbulence and mixing in Holmboe waves. J. Phys. Oceanogr. 33, 694–711.Google Scholar
Smyth, W. D., Klaassen, G. P. & Peltier, W. R. 1988 Finite amplitude Holmboe waves. Geophys. Astrophys. Fluid Dyn. 43 (2), 181–222.Google Scholar
Solheim, L. P. & Peltier, W. R. 1994 Avalanche effects in phase transition modulated thermal convection: a model of earth’s mantle. J. Geophys. Res. 99 (B4), 6997–7018.Google Scholar
Strang, E. J. & Fernando, H. J. S. 2001 Entrainment and mixing in stratified shear flows. J. Fluid Mech. 428, 349–386.Google Scholar
Taylor, G. I. 1915 Eddy motion in the atmosphere. Phil. Trans. R. Soc. A 215, 1–26.Google Scholar
Thorpe, S. A. & Liu, Z. 2009 Marginal instability? J. Phys. Oceanogr. 39 (9), 2373–2381.Google Scholar
Thorpe, S. A. 1968 A method of producing a shear flow in a stratified fluid. J. Fluid Mech. 32, 693–704.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar
Zhou, Q., Taylor, J. R. & Caulfield, C. P. 2017 Self-similar mixing in stratified plane Couette flow for varying Prandtl number. J. Fluid Mech. 820, 86–120.Google Scholar
Zhu, D. Z. & Lawrence, G. A. 2001 Holmboe’s instability in exchange flows. J. Fluid Mech. 429, 391–409.Google Scholar