Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T12:29:27.372Z Has data issue: false hasContentIssue false
  • English
  • Français

Sediment-laden fresh water above salt water: nonlinear simulations

Published online by Cambridge University Press:  27 November 2014

P. Burns  and
E. Meiburg
P. Burns
Affiliation:
Department of Mechanical Engineering, University of California, Santa Barbara, CA 93106, USA
E. Meiburg*
Affiliation:
Department of Mechanical Engineering, University of California, Santa Barbara, CA 93106, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

When a layer of particle-laden fresh water is placed above clear, saline water, both double-diffusive and Rayleigh–Taylor instabilities may arise. The present investigation extends the linear stability analysis of Burns & Meiburg (J. Fluid Mech., vol. 691, 2012, pp. 279–314) into the nonlinear regime, by means of two- and three-dimensional direct numerical simulations (DNS). The initial instability growth in the DNS is seen to be consistent with the dominant modes predicted by the linear stability analysis. The subsequent vigorous growth of individual fingers gives rise to a secondary instability, and eventually to the formation of intense plumes that become detached from the interfacial region. The simulations show that the presence of particles with a Stokes settling velocity modifies the traditional double-diffusive fingering by creating an unstable ‘nose region’ in the horizontally averaged profiles, located between the upward-moving salinity and the downward-moving sediment interface. The effective thickness 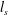$l_{s}$ (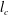$l_{c}$) of the salinity (sediment) interface grows diffusively, as does the height 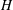$H$ of the nose region. The ratio 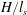$H/l_{s}$ initially grows and then plateaus, at a value that is determined by the balance between the flux of sediment into the rose region from above, the double-diffusive/Rayleigh–Taylor flux out of the nose region below, and the rate of sediment accumulation within the nose region. For small values of 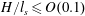$H/l_{s}\leqslant O(0.1)$, double-diffusive fingering dominates, while for larger values 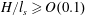$H/l_{s}\geqslant O(0.1)$ the sediment and salinity interfaces become increasingly separated in space and the dominant instability mode becomes Rayleigh–Taylor like. A scaling analysis based on the results of a parametric study indicates that 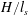$H/l_{s}$ is a linear function of a single dimensionless grouping that can be interpreted as the ratio of inflow and outflow of sediment into the nose region. The simulation results furthermore indicate that double-diffusive and Rayleigh–Taylor instability mechanisms cause the effective settling velocity of the sediment to scale with the overall buoyancy velocity of the system, which can be orders of magnitude larger than the Stokes settling velocity. While the power spectra of double-diffusive and Rayleigh–Taylor-dominated flows are qualitatively similar, the difference between flows dominated by fingering and leaking is clearly seen when analysing the spectral phase shift. For leaking-dominated flows a phase-locking mechanism is observed, which intensifies with time. Hence, the leaking mode can be interpreted as a fingering mode which has become phase-locked due to large-scale overturning events in the nose region, as a result of a Rayleigh–Taylor instability.

JFM classification

Convection: Double diffusive convection Instability: Parametric instability Geophysical and Geological Flows: Sediment transport
Type
Papers
Information
Journal of Fluid Mechanics , Volume 762 , 10 January 2015 , pp. 156 - 195
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.Google Scholar
Bosse, T., Kleiser, L. & Meiburg, E. 2006 Small particles in homogeneous turbulence: settling velocity enhancement by two-way coupling. Phys. Fluids 18, 027102.CrossRefGoogle Scholar
Burns, P.2013 Double-diffusive instabilities in sediment-laden systems. PhD thesis, UCSB.Google Scholar
Burns, P. & Meiburg, E. 2012 Sediment-laden fresh water above salt water: linear stability analysis. J. Fluid Mech. 691, 279–314.Google Scholar
Carey, S. 1997 Influence of convective sedimentation on the formation of widespread tephra fall layers in the deep sea. Geology 25, 839–842.2.3.CO;2>CrossRefGoogle Scholar
Chen, C. F. 1997 Particle flux through sediment fingers. Deep-Sea Res. 44, 1645–1654.CrossRefGoogle Scholar
Green, T. 1987 The importance of double diffusion to the settling of suspended material. Sedimentology 34, 319–331.CrossRefGoogle Scholar
Green, T. & Diez, T. 1995 Vertical plankton transport due to self-induced convection. J. Plankton Res. 17, 1723–1730.CrossRefGoogle Scholar
Henniger, R.2011 Direct and large-eddy simulation of particle transport processes in estuarine environments. PhD thesis, ETH-Zurich.Google Scholar
Henniger, R., Obrist, D. & Kleiser, L. 2012 High-order accurate solution of the incompressible Navier–Stokes equations on massively parallel computers. J. Comput. Phys. 229, 3543–3572.CrossRefGoogle Scholar
Hoyal, D. C., Bursik, M. I. & Atkinson, J. F. 1999a The influence of diffusive convection on sedimentation from buoyant plumes. Mar. Geol. 159, 205–220.CrossRefGoogle Scholar
Hoyal, D. C., Bursik, M. I. & Atkinson, J. F. 1999b Settling-driven convection: a mechanism of sedimentation from stratified fluids. J. Geophys. Res. 104, 7953–7966.Google Scholar
Huppert, H. E. & Manins, P. C. 1973 Limiting conditions for salt-fingering at an interface. Deep-Sea Res. 20, 315–323.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.Google Scholar
Manville, V. & Wilson, C. 2004 Vertical density currents: a review of their potential role in the deposition and interpretation of deep-sea ash layers. J. Geol. Soc. 161, 947–958.Google Scholar
Maxworthy, T. 1999 The dynamics of sedimenting surface gravity currents. J. Fluid Mech. 392, 27–44.Google Scholar
McDougall, T. & Taylor, J. 1984 Flux measurements across a finger interface at low values of the stability ratio. J. Mar. Res. 42, 1–14.Google Scholar
Milliman, J. D. & Syvitski, J. P. M. 1992 Geomorphic/tectonic control of sediment discharge to the ocean: the importance of small mountainous rivers. J. Geol. 100, 525–544.CrossRefGoogle Scholar
Mulder, T. & Syvitski, J. P. M. 1995 Turbidity currents generated at river mouths during exceptional discharges to the world oceans. J. Geol. 103 (3), 285–299.CrossRefGoogle Scholar
Parsons, J. D., Bush, J. W. M. & Syvitski, J. P. M. 2001 Hyperpycnal plume formation from riverine outflows with small sediment concentrations. Sedimentology 48, 465–478.Google Scholar
Parsons, J. D. & Garcia, M. H. 2000 Enhanced sediment scavenging due to double-diffusive convection. J. Sedim. Res. 70, 47–52.Google Scholar
Segre, P. N., Liu, F., Umbanhowar, P. & Weitz, D. 2001 An effective temperature for sedimentation. Nature 409, 594–597.Google Scholar
Smyth, W. D. & Kimura, S. 2007 Instability and diapycnal momentum transport in a double-diffusive, stratified shear layer. J. Phys. Oceanogr. 37 (6), 1551–1565.Google Scholar
Smyth, W. D. & Kimura, S. 2011 Mixing in a moderately sheared salt-fingering layer. J. Phys. Oceanogr. 41 (7), 1364–1384.Google Scholar
Stellmach, S., Traxler, A., Garaud, P., Brummell, N. & Radko, T. 2011 Dynamics of fingering convection. Part 2. The formation of thermohaline staircases. J. Fluid Mech. 677, 554–571.CrossRefGoogle Scholar
Stern, M. 1969 Collective instability of salt fingers. J. Fluid Mech. 35, 209–218.CrossRefGoogle Scholar
Traxler, A., Garaud, P. & Stellmach, S. 2012 Numerically determined transport laws for fingering (‘thermohaline’) convection in astrophysics. Astrophys. J. Lett. 728 (2), L29.Google Scholar
Traxler, A., Stellmach, S., Garaud, P., Radko, T. & Brummell, N. 2011 Dynamics of fingering convection. Part 1. Small-scale fluxes and large-scale instabilities. J. Fluid Mech. 677, 530–553.Google Scholar
Turner, J. S. 1967 Salt fingers across a density interface. Deep-Sea Res. 14, 599–611.Google Scholar
Williamson, J. 1980 Low-storage Runge–Kutta schemes. J. Comput. Phys. 35, 48–56.Google Scholar
Wray, A.1986 Very low storage time-advancement schemes. NASA Tech. Rep. NASA Ames Research Center.Google Scholar
Yu, X., Hsu, T.-J. & Balachandar, S. 2014 Convective instability in sedimentation: 3D numerical study. J. Geophys. Res. (submitted).Google Scholar