Article contents
Secondary instability and subcritical transition of the leading-edge boundary layer
Published online by Cambridge University Press: 04 March 2016
Abstract
The leading-edge boundary layer (LEBL) in the front part of swept airplane wings is prone to three-dimensional subcritical instability, which may lead to bypass transition. The resulting increase of airplane drag and fuel consumption implies a negative environmental impact. In the present paper, we present a temporal biglobal secondary stability analysis (SSA) and direct numerical simulations (DNS) of this flow to investigate a subcritical transition mechanism. The LEBL is modelled by the swept Hiemenz boundary layer (SHBL), with and without wall suction. We introduce a pair of steady, counter-rotating, streamwise vortices next to the attachment line as a generic primary disturbance. This generates a high-speed streak, which evolves slowly in the streamwise direction. The SSA predicts that this flow is unstable to secondary, time-dependent perturbations. We report the upper branch of the secondary neutral curve and describe numerous eigenmodes located inside the shear layers surrounding the primary high-speed streak and the vortices. We find secondary flow instability at Reynolds numbers as low as 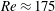 $Re\approx 175$, i.e. far below the linear critical Reynolds number
$Re\approx 175$, i.e. far below the linear critical Reynolds number 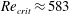 $Re_{crit}\approx 583$ of the SHBL. This secondary modal instability is confirmed by our three-dimensional DNS. Furthermore, these simulations show that the modes may grow until nonlinear processes lead to breakdown to turbulent flow for Reynolds numbers above
$Re_{crit}\approx 583$ of the SHBL. This secondary modal instability is confirmed by our three-dimensional DNS. Furthermore, these simulations show that the modes may grow until nonlinear processes lead to breakdown to turbulent flow for Reynolds numbers above 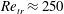 $Re_{tr}\approx 250$. The three-dimensional mode shapes, growth rates, and the frequency dependence of the secondary eigenmodes found by SSA and the DNS results are in close agreement with each other. The transition Reynolds number
$Re_{tr}\approx 250$. The three-dimensional mode shapes, growth rates, and the frequency dependence of the secondary eigenmodes found by SSA and the DNS results are in close agreement with each other. The transition Reynolds number 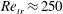 $Re_{tr}\approx 250$ at zero suction and its increase with wall suction closely coincide with experimental and numerical results from the literature. We conclude that the secondary instability and the transition scenario presented in this paper may serve as a possible explanation for the well-known subcritical transition observed in the leading-edge boundary layer.
$Re_{tr}\approx 250$ at zero suction and its increase with wall suction closely coincide with experimental and numerical results from the literature. We conclude that the secondary instability and the transition scenario presented in this paper may serve as a possible explanation for the well-known subcritical transition observed in the leading-edge boundary layer.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 7
- Cited by



