Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-16T17:02:37.574Z Has data issue: false hasContentIssue false
  • English
  • Français

Secondary instabilities of Görtler vortices in high-speed boundary layer flows

Published online by Cambridge University Press:  21 September 2015

Jie Ren  and
Song Fu
Jie Ren
Affiliation:
School of Aerospace Engineering, Tsinghua University, Beijing, 100084, China
Song Fu*
Affiliation:
School of Aerospace Engineering, Tsinghua University, Beijing, 100084, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Görtler vortices developed in laminar boundary layer experience remarkable changes when the flow is subjected to compressibility effects. In the present study, five 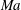$\mathit{Ma}$ numbers, covering incompressible to hypersonic flows, at 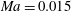$\mathit{Ma}=0.015$, 1.5, 3.0, 4.5 and 6.0 are specified to illustrate these effects. Görtler vortices in subsonic and moderate supersonic flows (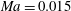$\mathit{Ma}=0.015$, 1.5 and 3.0) are governed by the conventional wall-layer mode (mode W). In hypersonic flows (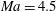$\mathit{Ma}=4.5$, 6.0), the trapped-layer mode (mode T) becomes dominant. This difference is maintained and intensifies downstream leading to different scenarios of secondary instabilities. The linear and nonlinear development of Görtler vortices which are governed by dominant modal disturbances are investigated with direct marching of the nonlinear parabolic equations. The secondary instabilities of Görtler vortices set in when the resulting streaks are adequately developed. They are studied with Floquet theory at multiple streamwise locations. The secondary perturbations become unstable downstream following the sequence of sinuous mode type I, varicose mode and sinuous mode type II, indicating an increasing threshold amplitude. Onset conditions are determined for these modes. The above three modes can each have the largest growth rate under the right conditions. In the hypersonic cases, the threshold amplitude 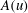$A(u)$ is dramatically reduced, showing the significant impact of the thermal streaks. To investigate the parametric effect of the spanwise wavenumber, three global wavenumbers ($B=0.5$, 1.0 and 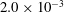$2.0\times 10^{-3}$) are specified. The relationship between the dominant mode (sinuous or varicose) and the spanwise wavenumber of Görtler vortices found in incompressible flows (Li & Malik, J. Fluid Mech., vol. 297, 1995, pp. 77–100) is shown to be not fully applicable in high-speed cases. The sinuous mode becomes the most dangerous, regardless of the spanwise wavelength when 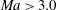$\mathit{Ma}>3.0$. The subharmonic type can be the most dangerous mode while the detuned type can be neglected, although some of the sub-dominant secondary modes reach their peak growth rates under detuned states.

JFM classification

Instability: Absolute/convective instability Compressible Flows: Compressible boundary layers Instability: Nonlinear instability
Type
Papers
Information
Journal of Fluid Mechanics , Volume 781 , 25 October 2015 , pp. 388 - 421
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, P., Berggren, M. & Henningson, D. S. 1999 Optimal disturbances and bypass transition in boundary layers. Phys. Fluids 11 (1), 134–150.CrossRefGoogle Scholar
Andersson, P., Brandt, L., Bottaro, A. & Henningson, D. S. 2001 On the breakdown of boundary layer streaks. J. Fluid Mech. 428, 29–60.CrossRefGoogle Scholar
Asai, M., Minagawa, M. & Nishioka, M. 2002 The instability and breakdown of a near-wall low-speed streak. J. Fluid Mech. 455, 289–314.CrossRefGoogle Scholar
Bassom, A. P. & Hall, P. 1994 The receptivity problem for $O(1)$ wavelength Görtler vortices. Proc. R. Soc. Lond. A 446 (1928), 499–516.Google Scholar
Bassom, A. P. & Seddougui, S. O. 1995 Receptivity mechanisms for Görtler vortex modes. Theor. Comput. Fluid Dyn. 7 (5), 317–339.CrossRefGoogle Scholar
Bonfigli, G. & Kloker, M. 2007 Secondary instability of crossflow vortices: validation of the stability theory by direct numerical simulation. J. Fluid Mech. 583, 229–272.CrossRefGoogle Scholar
Bottaro, A. & Klingmann, B. G. B. 1996 On the linear breakdown of Görtler vortices. Eur. J. Mech. (B/Fluids) 15 (3), 301–330.Google Scholar
Bottaro, A. & Luchini, P. 1999 Görtler vortices: Are they amenable to local eigenvalue analysis? Eur. J. Mech. (B/Fluids) 18 (1), 47–65.CrossRefGoogle Scholar
de la Chevalerie, D. A., Fonteneau, A., Luca, L. D. & Cardone, G. 1997 Görtler-type vortices in hypersonic flows: the ramp problem. Exp. Therm. Fluid Sci. 15 (2), 69–81.CrossRefGoogle Scholar
Chen, F.-J., Wilkinson, S. P. & Beckwith, I. E. 1993 Görtler instability and hypersonic quiet nozzle design. J. Spacecr. Rockets 30 (2), 170–175.CrossRefGoogle Scholar
Choudhari, M., Li, F., Chang, C.-L., Edwards, J., Kegerise, M. & King, R.2010 Laminar-turbulent transition behind discrete roughness elements in a high-speed boundary layer. In 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, AIAA-2010-1575. American Institute of Aeronautics and Astronautics (AIAA).CrossRefGoogle Scholar
Choudhari, M., Li, F., Chang, C.-L., Norris, A. & Edwards, J.2013 Wake instabilities behind discrete roughness elements in high speed boundary layers. In 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, AIAA-2013-0081.Google Scholar
Crouch, J. D. 1997 Excitation of secondary instabilities in boundary layers. J. Fluid Mech. 336, 245–266.CrossRefGoogle Scholar
Dando, A. H. & Seddougui, S. O. 1993 The compressible Görtler problem in two-dimensional boundary layers. IMA J. Appl. Maths 51 (1), 27–67.CrossRefGoogle Scholar
Day, H. P., Herbert, T. & Saric, W. S. 1990 Comparing local and marching analysis of Görtler instability. AIAA J. 28 (6), 1010–1015.CrossRefGoogle Scholar
Denier, J. P., Hall, P. & Seddougui, S. O. 1991 On the receptivity problem for Görtler vortices: vortex motions induced by wall roughness. Phil. Trans. R. Soc. Lond. A 335 (1636), 51–85.Google Scholar
De Tullio, N., Paredes, P., Sandham, N. D. & Theofilis, V. 2013 Laminar-turbulent transition induced by a discrete roughness element in a supersonic boundary layer. J. Fluid Mech. 735, 613–646.CrossRefGoogle Scholar
Dong, M. & Wu, X. 2013 On continuous spectra of the orr-sommerfeld/squire equations and entrainment of free-stream vortical disturbances. J. Fluid Mech. 732, 616–659.CrossRefGoogle Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18 (4), 487–488.CrossRefGoogle Scholar
Federov, A. & Tumin, A. 2011 High-speed boundary-layer instability: old terminology and a new framework. AIAA J. 49 (8), 1647–1657.CrossRefGoogle Scholar
Floryan, J. M. 1991 On the Görtler instability of boundary layers. Prog. Aerosp. Sci. 28 (3), 235–271.CrossRefGoogle Scholar
Fu, Y. & Hall, P. 1992 Nonlinear development and secondary instability of large-amplitude Görtler vortices in hypersonic boundary-layers. Eur. J. Mech. (B/Fluids) 11 (4), 465–510.Google Scholar
Fu, Y. & Hall, P. 1993 Effects of Görtler vortices, wall cooling and gas dissociation on the Rayleigh instability in a hypersonic boundary layer. J. Fluid Mech. 247, 503–525.CrossRefGoogle Scholar
Girgis, I. G. & Liu, J. T. C. 2006 Nonlinear mechanics of wavy instability of steady longitudinal vortices and its effect on skin friction rise in boundary layer flow. Phys. Fluids 18 (2), 024102.CrossRefGoogle Scholar
Görtler, H. 1940 Über eine dreidimensionale instabilität laminarer grenzschichten an konkaven wänden. Ges. D. Wiss. Göttingen, Nachr 1 (2), translated as ‘On the three-dimensional instability of laminar boundary layers on concave walls. NACA TM 1375, 1954’.Google Scholar
Goulpié, P., Klingmann, B. G. B. & Bottaro, A. 1996 Görtler vortices in boundary layers with streamwise pressure gradient: linear theory. Phys. Fluids 8 (2), 451–459.CrossRefGoogle Scholar
Groskopf, G., Kloker, M. J. & Marxen, O. 2010 Bi-global crossplane stability analysis of high-speed boundary-layer flows with discrete roughness. In 7th IUTAM Symposium on Laminar–Turbulent Transition (ed. Schlatter, P. & Henningson, D. S.), IUTAM Bookseries, vol. 18, pp. 171–176. Springer.CrossRefGoogle Scholar
Hall, P. 1982 Taylor–Gortler vortices in fully developed or boundary-layer flows: linear theory. J. Fluid Mech. 124, 475–494.CrossRefGoogle Scholar
Hall, P. 1983 The linear development of Görtler vortices in growing boundary layers. J. Fluid Mech. 130, 41–58.CrossRefGoogle Scholar
Hall, P. 1990 Görtler vortices in growing boundary layers: the leading edge receptivity problem, linear growth and the nonlinear breakdown stage. Mathematika 37, 151–189.CrossRefGoogle Scholar
Hall, P. & Fu, Y. 1989 On the Görtler vortex instability mechanism at hypersonic speeds. Theor. Comput. Fluid Dyn. 1 (3), 125–134.CrossRefGoogle Scholar
Hall, P. & Horseman, N. J. 1991 The linear inviscid secondary instability of longitudinal vortex structures in boundary layers. J. Fluid Mech. 232, 357–375.CrossRefGoogle Scholar
Hanifi, A., Schmid, P. J. & Henningson, D. S. 1996 Transient growth in compressible boundary layer flow. Phys. Fluids 8 (3), 826–837.CrossRefGoogle Scholar
Herbert, T. 1976 On the stability of the boundary layer along a concave wall. Arch. Mech. Stosowanej 28 (5–6), 1039–1055.Google Scholar
Herbert, T. 1988 Secondary instability of boundary layers. Annu. Rev. Fluid Mech. 20, 487–526.CrossRefGoogle Scholar
Hultgren, L. S. & Gustavsson, L. H. 1981 Algebraic growth of disturbances in a laminar boundary layer. Phys. Fluids 24 (6), 1000–1004.CrossRefGoogle Scholar
Joslin, R. D. & Grosch, C. E. 1995 Growth characteristics downstream of a shallow bump: computation and experiment. Phys. Fluids 7 (12), 3042–3047.CrossRefGoogle Scholar
Kegerise, M. A., King, R. A., Owens, L. R., Choudhari, M. M., Norris, A. T., Li, F. & Chang, C.-L.2012 An experimental and numerical study of roughness-induced instabilities in a Mach 3.5 boundary layer. In RTO AVT-200 RSM-030 Specialists’ Meeting on Hypersonic Laminar–Turbulent Transition, nF1676L-14423.Google Scholar
Landahl, M. T. 1975 Wave breakdown and turbulence. SIAM J. Appl. Maths 28 (4), 735–756.CrossRefGoogle Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.CrossRefGoogle Scholar
Lee, K. & Liu, J. T. C. 1992 On the growth of mushroomlike structures in nonlinear spatially developing Goertler vortex flow. Phys. Fluids A 4 (1), 95–103.CrossRefGoogle Scholar
Leib, S. J., Wundrow, D. W. & Goldstein, M. E. 1999 Effect of free-stream turbulence and other vortical disturbances on a laminar boundary layer. J. Fluid Mech. 380, 169–203.CrossRefGoogle Scholar
Li, F., Choudhari, M., Chang, C.-L., Wu, M. & Greene, P.2010 Development and breakdown of Görtler vortices in high speed boundary layers. In 50th Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, AIAA-2010-0705.Google Scholar
Li, F., Choudhari, M. M., Duan, L. & Chang, C.-L. 2014 Nonlinear development and secondary instability of traveling crossflow vortices. Phys. Fluids 26 (6), 064104.CrossRefGoogle Scholar
Li, F. & Malik, M. R. 1995 Fundamental and subharmonic secondary instabilities of Görtler vortices. J. Fluid Mech. 297, 77–100.CrossRefGoogle Scholar
Liu, W. & Domaradzki, J. A. 1993 Direct numerical simulation of transition to turbulence in Görtler flow. J. Fluid Mech. 246, 267–299.CrossRefGoogle Scholar
Luca, L., Cardone, G., Aymer de la Chevalerie, D. & Fonteneau, A. 1993 Goertler instability of a hypersonic boundary layer. Exp. Fluids 16 (1), 10–16.CrossRefGoogle Scholar
Luchini, P. 2000 Reynolds-number-independent instability of the boundary layer over a flat surface: optimal perturbations. J. Fluid Mech. 404, 289–309.CrossRefGoogle Scholar
Luchini, P. & Bottaro, A. 1998 Görtler vortices: a backward-in-time approach to the receptivity problem. J. Fluid Mech. 363, 1–23.CrossRefGoogle Scholar
Ma, Y. & Zhong, X. 2003 Receptivity of a supersonic boundary layer over a flat plate. Part 1. Wave structures and interactions. J. Fluid Mech. 488, 31–78.CrossRefGoogle Scholar
Mack, L. M. 1975 Linear stability theory and the problem of supersonic boundary-layer transition. AIAA J. 13 (3), 278–289.CrossRefGoogle Scholar
Mack, L. M.1984 Boundary-layer linear stability theory. Tech. Rep. DTIC Document.Google Scholar
Mitsudharmadi, H., Winoto, S. H. & Shah, D. A. 2005 Secondary instability in forced wavelength Görtler vortices. Phys. Fluids 17 (7), 074104.CrossRefGoogle Scholar
Morkovin, M. V. 1990 On roughness induced transition: facts, views, and speculations. In Instability and Transition (ed. Hussaini, M. Y. & Voigt, R. G.), pp. 281–295. Springer.Google Scholar
Park, D. S. & Huerre, P. 1995 Primary and secondary instabilities of the asymptotic suction boundary layer on a curved plate. J. Fluid Mech. 283, 249–272.CrossRefGoogle Scholar
Ren, J. & Fu, S. 2014a Competition of the multiple Görtler modes in hypersonic boundary layer flows. Sci. China Phys. Mech. Astron. 57 (6), 1178–1193.CrossRefGoogle Scholar
Ren, J. & Fu, S. 2014b Floquet analysis of fundamental, subharmonic and detuned secondary instabilities of Görtler vortices. Sci. China Phys. Mech. Astron. 57 (3), 555–561.CrossRefGoogle Scholar
Ren, J. & Fu, S. 2015 Study of the discrete spectrum in a Mach 4.5 Görtler flow. Flow Turbul. Combust. 94 (2), 339–357.CrossRefGoogle Scholar
Ricco, P., Luo, J. & Wu, X. 2011 Evolution and instability of unsteady nonlinear streaks generated by free-stream vortical disturbances. J. Fluid Mech. 677, 1–38.CrossRefGoogle Scholar
Ricco, P. & Wu, X. 2007 Response of a compressible laminar boundary layer to free-stream vortical disturbances. J. Fluid Mech. 587, 97–138.CrossRefGoogle Scholar
Sabry, A. S. & Liu, J. T. C. 1991 Longitudinal vorticity elements in boundary layers: nonlinear development from initial Görtler vortices as a prototype problem. J. Fluid Mech. 231, 615–663.CrossRefGoogle Scholar
Saric, W. S. 1994 Görtler vortices. Annu. Rev. Fluid Mech. 26 (1), 379–409.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 2001 Stability and Transition in Shear Flows. Springer.CrossRefGoogle Scholar
Schneider, S. P.1998 Design of a Mach-6 quiet-flow wind-tunnel nozzle using the e**n method for transition estimation. In 36th AIAA Aerospace Sciences Meeting and Exhibit, AIAA-1998-0547.Google Scholar
Schneider, S. P. 2008 Development of hypersonic quiet tunnels. J. Spacecr. Rockets 45 (4), 641–664.CrossRefGoogle Scholar
Schrader, L., Brandt, L. & Zaki, T. A. 2011 Receptivity, instability and breakdown of Görtler flow. J. Fluid Mech. 682, 362–396.CrossRefGoogle Scholar
Schrijer, F. 2010 Investigation of Görtler vortices in a hypersonic double compression ramp flow by means of infrared thermography. Quant. Infrared Thermograph. J. 7 (2), 201–215.CrossRefGoogle Scholar
Sescu, A. & Thompson, D. 2015 On the excitation of Götler vortices by distributed roughness elements. Theor. Comput. Fluid Dyn. 29 (1–2), 67–92.CrossRefGoogle Scholar
Spall, R.  E. & Malik, M.  R. 1989 Goertler vortices in supersonic and hypersonic boundary layers. Phys. Fluids A 1 (11), 1822–1835.CrossRefGoogle Scholar
Swearingen, J. D. & Blackwelder, R. F. 1987 The growth and breakdown of streamwise vortices in the presence of a wall. J. Fluid Mech. 182, 255–290.CrossRefGoogle Scholar
Tandiono, T., Winoto, S. H. & Shah, D. A. 2008 On the linear and nonlinear development of Görtler vortices. Phys. Fluids 20 (9), 094103.CrossRefGoogle Scholar
Tandiono, T., Winoto, S. H. & Shah, D.  A. 2009 Wall shear stress in Görtler vortex boundary layer flow. Phys. Fluids 21 (8), 084106.CrossRefGoogle Scholar
Tumin, A. & Reshotko, E. 2001 Spatial theory of optimal disturbances in boundary layers. Phys. Fluids 13 (7), 2097–2104.CrossRefGoogle Scholar
Tumin, A. & Reshotko, E. 2003 Optimal disturbances in compressible boundary layers. AIAA J. 41 (12), 2357–2363.CrossRefGoogle Scholar
Tumin, A. & Reshotko, E. 2005 Receptivity of a boundary-layer flow to a three-dimensional hump at finite Reynolds numbers. Phys. Fluids 17 (9), 094101.CrossRefGoogle Scholar
Wassermann, P. & Kloker, M. 2005 Transition mechanisms in a three-dimensional boundary-layer flow with pressure-gradient changeover. J. Fluid Mech. 530, 265–293.CrossRefGoogle Scholar
Whang, C. & Zhong, X.2001 Secondary Görtler instability in hypersonic boundary layers. In 39th Aerospace Sciences Meeting & Exhibit, AIAA-2001-0273.Google Scholar
Wu, X., Zhao, D. & Luo, J. 2011 Excitation of steady and unsteady Görtler vortices by free-stream vortical disturbances. J. Fluid Mech. 682, 66–100.CrossRefGoogle Scholar
Xu, G., Liu, G. & Jiang, X.2014 The nonlinear instability of the supersonic crossflow vortex. In 44th AIAA Fluid Dynamics Conference, AIAA-2014-2637.Google Scholar
Yu, X. & Liu, J. T. C. 1991 The secondary instability in Göertler flow. Phys. Fluids A 3 (8), 1845–1847.CrossRefGoogle Scholar
Yu, X. & Liu, J. T. C. 1994 On the mechanism of sinuous and varicose modes in three-dimensional viscous secondary instability of nonlinear Görtler rolls. Phys. Fluids 6 (2), 736–750.CrossRefGoogle Scholar