Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-06T00:25:40.678Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling of separated shear layers: an investigation of mass entrainment

Published online by Cambridge University Press:  15 August 2017

Francesco Stella ,
Nicolas Mazellier Open the ORCID record for Nicolas Mazellier [Opens in a new window]  and
Azeddine Kourta
Francesco Stella
Affiliation:
University of Orléans, INSA-CVL, PRISME, EA 4229, F45072, Orléans, France
Nicolas Mazellier*
Affiliation:
University of Orléans, INSA-CVL, PRISME, EA 4229, F45072, Orléans, France
Azeddine Kourta
Affiliation:
University of Orléans, INSA-CVL, PRISME, EA 4229, F45072, Orléans, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

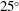We report an experimental investigation of the separating/reattaching flow over a descending ramp with a $25^{\circ }$ expansion angle. Emphasis is given to mass entrainment through the boundaries of the separated shear layer emanating from the upper edge of the ramp. For this purpose, the turbulent/non-turbulent interface and the separation line inferred from image-based analysis are used respectively to mark the upper and lower bounds of the separated shear layer. The main objective of this study is to identify the physical parameters that scale the development of the separated shear layer, by giving a specific emphasis to the investigation of mass entrainment. Our results emphasise the multiscale nature of mass entrainment through the separated shear layer. The recirculation length 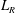$L_{R}$, step height 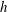$h$ and free-stream velocity 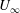$U_{\infty }$ are the dominant scales that organise the separated flow (and related large-scale quantities as pressure distribution or shear layer growth rate) and set mean mass fluxes. However, local viscous mechanisms seem to be responsible for most of local mass entrainment. Furthermore, it is shown that large-scale mass entrainment is driven by incoming boundary layer properties, since 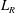$L_{R}$ scales with 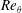$Re_{\unicode[STIX]{x1D703}}$, and in particular by its turbulent state. Surprisingly, the relationships evidenced in this study suggest that these dependencies are established over a large distance upstream of separation and that they might also extend to small scales, at which viscous entrainment is dominant. If confirmed by additional studies, our findings would open new perspectives for designing effective separation control systems.

JFM classification

Boundary Layers: Boundary Layers Wakes/Jets: Separated flows Turbulent Flows: Shear layer turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 851 - 887
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, E. W. & Johnston, J. P. 1988a Effects of the separating shear layer on the reattachment flow structure Part 1: pressure and turbulence quantities. Exp. Fluids 6 (6), 400–408.Google Scholar
Adams, E. W. & Johnston, J. P. 1988b Effects of the separating shear layer on the reattachment flow structure part 2: reattachment length and wall shear stress. Exp. Fluids 6 (7), 493–499.Google Scholar
Bell, J. H. & Mehta, R. D.1988 Contraction design for small low-speed wind tunnels. NASA STI/Recon Tech. Rep. No 89, 13753.Google Scholar
Bisset, D. K., Hunt, J. C. R. & Rogers, M. M. 2002 The turbulent/non-turbulent interface bounding a far wake. J. Fluid Mech. 451, 383–410.CrossRefGoogle Scholar
Brassard, D. & Ferchichi, M. 2005 Transformation of a polynomial for a contraction wall profile. Trans. ASME J. Fluids Engng 127 (1), 183–185.Google Scholar
Browand, F. K. & Troutt, T. R. 1985 The turbulent mixing layer: geometry of large vortices. J. Fluid Mech. 158, 489–509.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (04), 775–816.Google Scholar
Chapman, D. R., Kuehn, D. M. & Larson, H. K.1958 Investigation of separated flows in supersonic and subsonic streams with emphasis on the effect of transition. NACA Tech. Rep. TN-1356.Google Scholar
Chauhan, K., Monkewitz, P. A. & Nagib, H. M. 2009 Criteria for assessing experiments in zero pressure gradient boundary layers. Fluid Dyn. Res. 41 (2), 021404.Google Scholar
Chauhan, K., Philip, J., de Silva, C. M., Hutchins, N. & Marusic, I. 2014 The turbulent/non-turbulent interface and entrainment in a boundary layer. J. Fluid Mech. 742, 119–151.CrossRefGoogle Scholar
Cherry, E. M., Elkins, C. J. & Eaton, J. K. 2008 Geometric sensitivity of three-dimensional separated flows. Intl J. Heat Fluid Flow 29 (3), 803–811.Google Scholar
Cintosun, E., Smallwood, G. J. & Gülder, O. L. 2007 Flame surface fractal characteristics in premixed turbulent combustion at high turbulence intensities. AIAA J. 45 (11), 2785–2789.CrossRefGoogle Scholar
Corrsin, S. & Kistler, A. L.1955 Free-stream boundaries of turbulent flows. NACA Tech. Rep. TN-1244.Google Scholar
Cuvier, C.2012 Active control of a separated turbulent boundary layer in adverse pressure gradient. PhD thesis, École Centrale de Lille, Lille, France.Google Scholar
Cuvier, C., Braud, C., Foucaut, J. M. & Stanislas, M. 2011 Characterization of a separated turbulent boundary layer for flow control purpose. In 7th International Symposium on Turbulence and Shear Flow Phenomena (TSFP-7). Begell House Inc.Google Scholar
Dandois, J., Garnier, E. & Sagaut, P. 2007 Numerical simulation of active separation control by a synthetic jet. J. Fluid Mech. 574, 25–58.CrossRefGoogle Scholar
Eaton, J. K. & Johnston, J. P. 1981 A review of research on subsonic turbulent flow reattachment. AIAA J. 19 (9), 1093–1100.Google Scholar
Foucaut, J. M., Carlier, J. & Stanislas, M. 2004 PIV optimization for the study of turbulent flow using spectral analysis. Meas. Sci. Technol. 15 (6), 1046.Google Scholar
Garnier, E., Pamart, P. Y., Dandois, J. & Sagaut, P. 2012 Evaluation of the unsteady RANS capabilities for separated flows control. Comput. Fluids 61, 39–45.Google Scholar
Holzner, M. & Lüthi, B. 2011 Laminar superlayer at the turbulence boundary. Phys. Rev. Lett. 106 (13), 134503.Google Scholar
Joseph, P., Stella, F., Mazellier, N. & Kourta, A. 2016 Flow separation control on a 2d backward facing ramp using synthetic jets. In Second International Conference in Numerical and Experimental Aerodynamics of Road Vehicles and Trains (Aerovehicles 2).Google Scholar
Kourta, A., Thacker, A. & Joussot, R. 2015 Analysis and characterization of ramp flow separation. Exp. Fluids 56 (5), 1–14.Google Scholar
Krug, D., Holzner, M., Lüthi, B., Wolf, M., Kinzelbach, W. & Tsinober, A. 2015 The turbulent/non-turbulent interface in an inclined dense gravity current. J. Fluid Mech. 765, 303–324.CrossRefGoogle Scholar
Kumar, V. & Alvi, F. S.2005 Efficient control of separation using microjets. AIAA Paper 4879, 6–9.Google Scholar
Kwon, Y. S., Philip, J., Silva, C. M. de, Hutchins, N. & Monty, J. P. 2014 The quiescent core of turbulent channel flow. J. Fluid Mech. 751, 228–254.Google Scholar
Le, H., Moin, P. & Kim, J. 1997 Direct numerical simulation of turbulent flow over a backward-facing step. J. Fluid Mech. 330, 349–374.Google Scholar
Ligrani, P. M. & Bradshaw, P. 1987 Spatial resolution and measurement of turbulence in the viscous sublayer using subminiature hot-wire probes. Exp. Fluids 5 (6), 407–417.CrossRefGoogle Scholar
Marusic, I., Monty, J. P., Hultmark, M. & Smits, A. J. 2013 On the logarithmic region in wall turbulence. J. Fluid Mech. 716, R3.Google Scholar
Maurice, G., Thiesset, F., Halter, F., Mazellier, N., Chauveau, C., Gökalp, I. & Kourta, A. 2016 Scale analysis of the flame front in premixed combustion using Proper Orthogonal Decomposition. Exp. Therm. Fluid Sci. 73, 109–114.Google Scholar
Mazellier, N. & Vassilicos, J. C. 2010 Turbulence without Richardson–Kolmogorov cascade. Phys. Fluids 22 (7), 075101.CrossRefGoogle Scholar
McCormick, D. C.2000 Boundary layer separation control with directed synthetic jets. AIAA Paper 519.CrossRefGoogle Scholar
Meneveau, C. & Sreenivasan, K. R. 1990 Interface dimension in intermittent turbulence. Phys. Rev. A 41 (4), 2246–2248.CrossRefGoogle ScholarPubMed
Mistry, D., Philip, J., Dawson, J. R. & Marusic, I. 2016 Entrainment at multi-scales across the turbulent/non-turbulent interface in an axisymmetric jet. J. Fluid Mech. 802, 690–725.Google Scholar
Nadge, P. M. & Govardhan, R. N. 2014 High Reynolds number flow over a backward-facing step: structure of the mean separation bubble. Exp. Fluids 55 (1), 1–22.Google Scholar
Neumann, J. & Wengle, H. 2003 DNS and LES of passively controlled turbulent backward-facing step flow. Flow Turbul. Combust. 71 (1–4), 297–310.Google Scholar
Örlü, R. & Alfredsson, P. H. 2010 On spatial resolution issues related to time-averaged quantities using hot-wire anemometry. Exp. Fluids 49 (1), 101–110.Google Scholar
Philip, J., Hutchins, N., Monty, J. P. & Marusic, I. 2013 Spatial averaging of velocity measurements in wall-bounded turbulence: single hot-wires. Meas. Sci. Technol. 24 (11), 115301.Google Scholar
Philip, J., Meneveau, C., Silva, C. M. de & Marusic, I. 2014 Multiscale analysis of fluxes at the turbulent/non-turbulent interface in high Reynolds number boundary layers. Phys. Fluids 26 (1), 015105.Google Scholar
Pope, S. B. 1988 The evolution of surfaces in turbulence. Intl J. Engng Sci. 26 (5), 445–469.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Roshko, A. & Lau, J. C. 1965 Some observations on transition and reattachment of a free shear layer in incompressible flow. In Proceedings of the Heat Transfer and Fluid Mechanics Institute, vol. 18, p. 157. Stanford University Press.Google Scholar
Schlatter, P. & Örlü, R. 2010 Assessment of direct numerical simulation data of turbulent boundary layers. J. Fluid Mech. 659, 116–126.CrossRefGoogle Scholar
Sigurdson, L. W. 1995 The structure and control of a turbulent reattaching flow. J. Fluid Mech. 298, 139–165.Google Scholar
da Silva, C. B. & Pereira, J. C. F. 2008 Invariants of the velocity-gradient, rate-of-strain, and rate-of-rotation tensors across the turbulent/nonturbulent interface in jets. Phys. Fluids 20 (5), 055101.Google Scholar
da Silva, C. B. & Taveira, R. R. 2010 The thickness of the turbulent/nonturbulent interface is equal to the radius of the large vorticity structures near the edge of the shear layer. Phys. Fluids 22 (12), 121702.CrossRefGoogle Scholar
de Silva, C. M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent–nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111 (4), 044501.Google Scholar
Simpson, R. L. 1989 Turbulent boundary-layer separation. Annu. Rev. Fluid Mech. 21 (1), 205–232.Google Scholar
Song, S. & Eaton, J. K. 2003 Reynolds number effects on a turbulent boundary layer with separation, reattachment, and recovery. Exp. Fluids 36 (2), 246–258.Google Scholar
Song, S. & Eaton, J. K. 2004 Flow structures of a separating, reattaching, and recovering boundary layer for a large range of Reynolds number. Exp. Fluids 36 (4), 642–653.Google Scholar
Sreenivasan, K. R. & Meneveau, C. 1986 The fractal facets of turbulence. J. Fluid Mech. 173, 357–386.CrossRefGoogle Scholar
Sreenivasan, K. R., Ramshankar, R. & Meneveau, C. 1989 Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Proc. R. Soc. Lond. A 421 (1860), 79–108.Google Scholar
Thiesset, F., Maurice, G., Halter, F., Mazellier, N., Chauveau, C. & Gökalp, I. 2016 Geometrical properties of turbulent premixed flames and other corrugated interfaces. Phys. Rev. E 93, 013116.Google Scholar
Veynante, D., Lodato, G., Domingo, P., Vervisch, L. & Hawkes, E. R. 2010 Estimation of three-dimensional flame surface densities from planar images in turbulent premixed combustion. Exp. Fluids 49 (1), 267–278.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2005 Mechanics of the turbulent–nonturbulent interface of a Jet. Phys. Rev. Lett. 95 (17), 174501.Google Scholar
Westerweel, J., Fukushima, C., Pedersen, J. M. & Hunt, J. C. R. 2009 Momentum and scalar transport at the turbulent/non-turbulent interface of a jet. J. Fluid Mech. 631, 199–230.Google Scholar
Wiltse, J. M. & Glezer, A. 1993 Manipulation of free shear flows using piezoelectric actuators. J. Fluid Mech. 249, 261–285.Google Scholar
Wyngaard, J. C. 1968 Measurement of small-scale turbulence structure with hot wires. J. Phys. E 1 (11), 1105.Google Scholar