Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T00:05:57.672Z Has data issue: false hasContentIssue false
  • English
  • Français

Scaling laws for migrating cloud of low-Reynolds-number particles with Coulomb repulsion

Published online by Cambridge University Press:  28 November 2017

Sheng Chen ,
Wenwei Liu  and
Shuiqing Li Open the ORCID record for Shuiqing Li [Opens in a new window]
Sheng Chen
Affiliation:
Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Thermal Engineering, Tsinghua University, Beijing 100084, China
Wenwei Liu
Affiliation:
Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Thermal Engineering, Tsinghua University, Beijing 100084, China
Shuiqing Li*
Affiliation:
Key Laboratory for Thermal Science and Power Engineering of Ministry of Education, Department of Thermal Engineering, Tsinghua University, Beijing 100084, China
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the evolution of spherical clouds of charged particles that migrate under the action of a uniform external electrostatic field. Hydrodynamic interactions are modelled by Oseen equations and the Coulomb repulsion is calculated through pairwise summation. 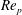It is shown that strong long-range Coulomb repulsion can prevent the breakup of the clouds covering a wide range of particle Reynolds number $Re_{p}$ and cloud-to-particle size ratio 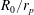$R_{0}/r_{p}$. A dimensionless charge parameter $\unicode[STIX]{x1D705}_{q}$ is constructed to quantify the effect of the repulsion, and a critical value $\unicode[STIX]{x1D705}_{q,t}$ is deduced, which successfully captures the transition of a cloud from hydrodynamically controlled regime to repulsion-controlled regime. Our results also reveal that, with sufficiently strong repulsion, the cloud undergoes a universal self-similar expansion. Scaling laws of cloud radius 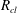$R_{cl}$ and particle number density $n$ are obtained by solving a continuum convection equation.

JFM classification

Multiphase and Particle-laden Flows: Multiphase flow Multiphase and Particle-laden Flows: Particle/fluid flow Complex Fluids: Suspensions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 835 , 25 January 2018 , pp. 880 - 897
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agbangla, G. C., Bacchin, P. & Climent, E. 2014 Collective dynamics of flowing colloids during pore clogging. Soft Matt. 10 (33), 6303–6315.Google Scholar
Batchelor, G. K. 2000 An Introduction to Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Bosse, T., Kleiser, L., Härtel, C. & Meiburg, E. 2005 Numerical simulation of finite Reynolds number suspension drops settling under gravity. Phys. Fluids 17 (3), 037101.Google Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20 (1), 111–157.CrossRefGoogle Scholar
Chen, S., Li, S. Q., Liu, W. & Makse, H. 2016a Effect of long-range repulsive Coulomb interactions on packing structure of adhesive particles. Soft Matt. 12 (6), 1836–1846.Google Scholar
Chen, S., Liu, W. & Li, S. Q. 2016b Effect of long-range electrostatic repulsion on pore clogging during microfiltration. Phys. Rev. E 94 (6), 063108.Google Scholar
Chraibi, H. & Amarouchene, Y. 2013 Sedimentation of granular columns in the viscous and weakly inertial regimes. Phys. Rev. E 88 (4), 042204.Google ScholarPubMed
Cordelair, J. & Greil, P. 2004 Discrete element modeling of solid formation during electrophoretic deposition. J. Mater. Sci. 39 (3), 1017–1021.CrossRefGoogle Scholar
Faletra, M., Marshall, J. S., Yang, M. & Li, S. Q. 2015 Particle segregation in falling polydisperse suspension droplets. J. Fluid Mech. 769, 79–102.Google Scholar
Guazzelli, E. & Morris, J. F. 2011 A Physical Introduction to Suspension Dynamics, Cambridge Texts in Applied Mathematics, vol. 45. Cambridge University Press.Google Scholar
Hamid, A., Molina, J. J. & Yamamoto, R. 2013 Sedimentation of non-Brownian spheres at high volume fractions. Soft Matt. 9 (42), 10056–10068.CrossRefGoogle Scholar
Ho, T. X., Phan-Thien, N. & Khoo, B. C. 2016 Destabilization of clouds of monodisperse and polydisperse particles falling in a quiescent and viscous fluid. Phys. Fluids 28 (6), 063305.Google Scholar
Izvekova, Y. N. & Popel, S. I. 2016 Charged dust motion in dust devils on Earth and Mars. Contrib. Plasma Phys. 56 (3–4), 263–269.Google Scholar
Jones, T. B. 2005 Electromechanics of Particles. Cambridge University Press.Google Scholar
Klix, C. L., Royall, C. P. & Tanaka, H. 2010 Structural and dynamical features of multiple metastable glassy states in a colloidal system with competing interactions. Phys. Rev. Lett. 104 (16), 165702.CrossRefGoogle Scholar
Lindsay, H. M. & Chaikin, P. M. 1982 Elastic properties of colloidal crystals and glasses. J. Chem. Phys. 76 (7), 3774–3781.CrossRefGoogle Scholar
Lu, J., Nordsiek, H., Saw, E. W. & Shaw, R. A. 2010 Clustering of charged inertial particles in turbulence. Phys. Rev. Lett. 104 (18), 184505.Google Scholar
Marshall, J. S. & Li, S. Q. 2014 Adhesive Particle Flow: A Discrete-Element Approach. Cambridge University Press.CrossRefGoogle Scholar
Matthews, L. S., Shotorban, B. & Truell, H. T. 2013 Cosmic dust aggregation with stochastic charging. Astrophys. J. 776 (2), 103.Google Scholar
Metzger, B., Nicolas, M. & Guazzelli, E. 2007 Falling clouds of particles in viscous fluids. J. Fluid Mech. 580, 283–301.Google Scholar
Nazockdast, E. & Morris, J. F. 2012 Effect of repulsive interactions on structure and rheology of sheared colloidal dispersions. Soft Matt. 8 (15), 4223–4234.CrossRefGoogle Scholar
Nitsche, J. M. & Batchelor, G. K. 1997 Break-up of a falling drop containing dispersed particles. J. Fluid Mech. 340, 161–175.Google Scholar
Pignatel, F., Nicolas, M. & Guazzelli, E. 2011 A falling cloud of particles at a small but finite Reynolds number. J. Fluid Mech. 671, 34–51.Google Scholar
Ruzicka, B. A. & Zaccarelli, E. 2011 A fresh look at the laponite phase diagram. Soft Matt. 7 (4), 1268–1286.Google Scholar
Schella, A., Herminghaus, S. & Schröter, M. 2017 Influence of humidity on tribo-electric charging and segregation in shaken granular media. Soft Matt. 13 (2), 394–401.Google Scholar
Sendekie, Z. B. & Bacchin, P. 2016 Colloidal jamming dynamics in microchannel bottlenecks. Langmuir 32 (6), 1478–1488.Google Scholar
Subramanian, G. & Koch, D. L. 2008 Evolution of clusters of sedimenting low-Reynolds-number particles with Oseen interactions. J. Fluid Mech. 603, 63–100.CrossRefGoogle Scholar
Tao, S., Guo, Z. & Wang, L. 2017 Numerical study on the sedimentation of single and multiple slippery particles in a Newtonian fluid. Powder Technol. 315, 126–138.CrossRefGoogle Scholar
Yang, M., Li, S. Q. & Marshall, J. S. 2015 Effects of long-range particle–particle hydrodynamic interaction on the settling of aerosol particle clouds. J. Aero. Sci. 90, 154–160.CrossRefGoogle Scholar