Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-26T08:32:07.976Z Has data issue: false hasContentIssue false
  • English
  • Français

A scaling law for the shear-production range of second-order structure functions

Published online by Cambridge University Press:  25 July 2016

Y. Pan  and
M. Chamecki
Y. Pan
Affiliation:
Department of Meteorology, Pennsylvania State University, University Park, PA 16802, USA
M. Chamecki*
Affiliation:
Department of Meteorology, Pennsylvania State University, University Park, PA 16802, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

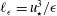Dimensional analysis suggests that the dissipation length scale ($\ell _{{\it\epsilon}}=u_{\star }^{3}/{\it\epsilon}$) is the appropriate scale for the shear-production range of the second-order streamwise structure function in neutrally stratified turbulent shear flows near solid boundaries, including smooth- and rough-wall boundary layers and shear layers above canopies (e.g. crops, forests and cities). These flows have two major characteristics in common: (i) a single velocity scale, i.e. the friction velocity (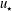$u_{\star }$) and (ii) the presence of large eddies that scale with an external length scale much larger than the local integral length scale. No assumptions are made about the local integral scale, which is shown to be proportional to 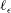$\ell _{{\it\epsilon}}$ for the scaling analysis to be consistent with Kolmogorov’s result for the inertial subrange. Here ${\it\epsilon}$ is the rate of dissipation of turbulent kinetic energy (TKE) that represents the rate of energy cascade in the inertial subrange. The scaling yields a log-law dependence of the second-order streamwise structure function on (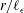$r/\ell _{{\it\epsilon}}$), where $r$ is the streamwise spatial separation. This scaling law is confirmed by large-eddy simulation (LES) results in the roughness sublayer above a model canopy, where the imbalance between local production and dissipation of TKE is much greater than in the inertial layer of wall turbulence and the local integral scale is affected by two external length scales. Parameters estimated for the log-law dependence on (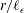$r/\ell _{{\it\epsilon}}$) are in reasonable agreement with those reported for the inertial layer of wall turbulence. This leads to two important conclusions. Firstly, the validity of the 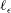$\ell _{{\it\epsilon}}$-scaling is extended to shear flows with a much greater imbalance between production and dissipation, indicating possible universality of the shear-production range in flows near solid boundaries. Secondly, from a modelling perspective, 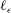$\ell _{{\it\epsilon}}$ is the appropriate scale to characterize turbulence in shear flows with multiple externally imposed length scales.

JFM classification

Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulence theory Turbulent Flows: Turbulent boundary layers
Type
Papers
Information
Journal of Fluid Mechanics , Volume 801 , 25 August 2016 , pp. 459 - 474
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alben, S., Shelley, M. & Zhang, J. 2002 Drag reduction through self-similar bending of a flexible body. Nature 420, 479–481.CrossRefGoogle ScholarPubMed
Bou-Zeid, E., Higgins, C., Huwald, H., Meneveau, C. & Parlange, M. B. 2010 Field study of the dynamics and modelling of subgrid-scale turbulence in a stable atmospheric surface layer over a glacier. J. Fluid Mech. 665, 480–515.CrossRefGoogle Scholar
Bou-Zeid, E., Meneveau, C. & Parlange, M. B. 2005 A scale-dependent Lagrangian dynamic model for large eddy simulation of complex turbulent flows. Phys. Fluids 17, 025105.Google Scholar
Chamecki, M. 2013 Persistence of velocity fluctuations in non-Gaussian turbulence within and above plant canopies. Phys. Fluids 25, 1–14.Google Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. 657 pp. Oxford University Press.Google Scholar
Davidson, P. A. & Krogstad, P.-Å. 2009 A simple model for the streamwise fluctuations in the log-law region of a boundary layer. Phys. Fluids 21, 055105.Google Scholar
Davidson, P. A. & Krogstad, P.-Å. 2014 A universal scaling for low-order structure functions in the log-law region of smooth-and rough-wall boundary layers. J. Fluid Mech. 752, 140–156.CrossRefGoogle Scholar
Davidson, P. A., Nickels, T. B. & Krogstad, P.-Å. 2006 The logarithmic structure function law in wall-layer turbulence. J. Fluid Mech. 550, 51–60.CrossRefGoogle Scholar
Gleicher, S. C., Chamecki, M., Isard, S. A., Pan, Y. & Katul, G. G. 2014 Interpreting three-dimensional spore concentration measurements and escape fraction in a crop canopy using a coupled Eulerian–Lagrangian Stochastic model. Agric. Forest Meteorol. 194, 118–131.Google Scholar
Gosselin, F., de Langre, E. & Machado-Almeida, B. A. 2010 Drag reduction of flexible plates by reconfiguration. J. Fluid Mech. 650, 319–341.Google Scholar
Horst, T. W. & Oncley, S. P. 2006 Corrections to inertial-range power spectra measured by CSAT3 and Solent sonic anemometers. 1: path-averaging errors. Boundary-Layer Meteorol. 119, 375–395.Google Scholar
van Hout, R., Zhu, W., Luznik, L., Katz, J., Kleissl, J. & Parlange, M. B. 2007 PIV measurements in the atmospheric boundary layer within and above a mature corn canopy. Part I: statistics and energy flux. J. Atmos. Sci. 64, 2805–2824.Google Scholar
Jackson, P. S. 1981 On the displacement height in the logarithmic velocity profile. J. Fluid Mech. 111, 15–25.Google Scholar
Kaimal, J. C. & Finnigan, J. J. 1994 Atmospheric Boundary Layer Flows: Their Structure and Measurement. 289 pp. Oxford University Press.Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Liu, S., Meneveau, C. & Katz, J. 1994 On the properties of similarity subgrid-scale models as deduced from measurements in a turbulent jet. J. Fluid Mech. 275, 83–119.Google Scholar
Muschinski, A. 1996 A similarity theory of locally homogeneous and isotropic turbulence generated by a Smagorinsky-type LES. J. Fluid Mech. 325, 239–260.Google Scholar
Pan, Y., Chamecki, M. & Isard, S. A. 2014a Large-eddy simulation of turbulence and particle dispersion inside the canopy roughness sublayer. J. Fluid Mech. 753, 499–534.Google Scholar
Pan, Y., Chamecki, M. & Nepf, H. M. 2016 Estimating the instantaneous drag-wind relationship for a horizontally homogeneous canopy. Boundary-Layer Meteorol. 160, 63–82.CrossRefGoogle Scholar
Pan, Y., Follett, E., Chamecki, M. & Nepf, H. 2014b Strong and weak, unsteady reconfiguration and its impact on turbulence structure within plant canopies. Phys. Fluids 26, 105102.CrossRefGoogle Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.Google Scholar
Poggi, D., Porporato, A., Ridolfi, L., Albertson, J. D. & Katul, G. G. 2004 The effect of vegetation density on canopy sub-layer turbulence. Boundary-Layer Meteorol. 111, 565–587.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. 771 pp. Cambridge University Press.CrossRefGoogle Scholar
Raupach, M. R., Finnigan, J. J. & Brunet, Y. 1996 Coherent eddies and turbulence in vegetation canopies: the mixing-layer analogy. Boundary-Layer Meteorol. 78, 351–382.Google Scholar
Raupach, M. R. & Thom, A. S. 1981 Turbulence in and above plant canopies. Annu. Rev. Fluid Mech. 13, 97–129.Google Scholar
Rogers, M. M. & Moser, R. D. 1994 Direct simulation of a self-similar turbulent mixing layer. Phys. Fluids 6, 903–923.CrossRefGoogle Scholar
Scotti, A., Meneveau, C. & Lilly, D. K. 1993 Generalized smagorinsky model for anisotropic grids. Phys. Fluids 5, 2306–2308.Google Scholar
Shaw, R. H., Silversides, R. H. & Thurtell, G. W. 1974 Some observations of turbulence and turbulent transport within and above plant canopies. Boundary-Layer Meteorol. 5, 429–449.Google Scholar
de Silva, C. M., Marusic, I., Woodcock, J. D. & Meneveau, C. 2015 Scaling of second-and higher-order structure functions in turbulent boundary layers. J. Fluid Mech. 769, 654–686.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. 300 pp. MIT Press.Google Scholar
Thom, A. S. 1971 Momentum absorption by vegetation. Q. J. R. Meteorol. Soc. 97, 414–428.Google Scholar
Townsend, A. A. 1958 Turbulent flow in a stably stratified atmosphere. J. Fluid Mech. 3, 361–372.Google Scholar
Wilson, J. D., Ward, D. P., Thurtell, G. W. & Kidd, G. E. 1982 Statistics of atmospheric turbulence within and above a corn canopy. Boundary-Layer Meteorol. 24, 495–519.Google Scholar