Article contents
Scaling behaviour in impulsively started viscous flow past a finite flat plate
Published online by Cambridge University Press: 04 September 2014
Abstract
Viscous flow past a finite flat plate which is impulsively started in the direction normal to itself is studied numerically using a high-order mixed finite-difference and semi-Lagrangian scheme. The goal is to resolve the details of the vorticity generation, and to determine the dependence of the flow on time and Reynolds number. Vorticity contours, streaklines and streamlines are presented for a range of times 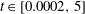 $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}t\in [0.0002,5]$ and Reynolds numbers
$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}t\in [0.0002,5]$ and Reynolds numbers 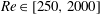 $\mathit{Re}\in [250,2000]$, non-dimensionalized with respect to the driving velocity and the plate length. At early times, the starting vortex is small relative to the plate length and is expected to grow as if an external length scale were absent. We identify three different types of scaling behaviours consistent with this premise. (i) At early times, solutions with different values of
$\mathit{Re}\in [250,2000]$, non-dimensionalized with respect to the driving velocity and the plate length. At early times, the starting vortex is small relative to the plate length and is expected to grow as if an external length scale were absent. We identify three different types of scaling behaviours consistent with this premise. (i) At early times, solutions with different values of 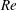 $\mathit{Re}$ are identical up to rescaling. (ii) The solution for fixed
$\mathit{Re}$ are identical up to rescaling. (ii) The solution for fixed 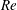 $\mathit{Re}$ satisfies a viscous similarity law in time, locally in space, as illustrated by the core vorticity maximum, the upstream boundary layer thickness, and the maximum speed, in three different regions of the flow. (iii) The vortex core trajectory and the shed circulation satisfy inviscid scaling laws for several decades in time, and are consequently essentially
$\mathit{Re}$ satisfies a viscous similarity law in time, locally in space, as illustrated by the core vorticity maximum, the upstream boundary layer thickness, and the maximum speed, in three different regions of the flow. (iii) The vortex core trajectory and the shed circulation satisfy inviscid scaling laws for several decades in time, and are consequently essentially 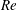 $\mathit{Re}$-independent at these times. In addition, the computed induced drag and tangential forces are found to follow approximate scaling laws that define their dependence on time and
$\mathit{Re}$-independent at these times. In addition, the computed induced drag and tangential forces are found to follow approximate scaling laws that define their dependence on time and 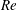 $\mathit{Re}$.
$\mathit{Re}$.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2014 Cambridge University Press
References
- 14
- Cited by


