Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-17T19:07:29.625Z Has data issue: false hasContentIssue false
  • English
  • Français

Scale interactions in a mixing layer – the role of the large-scale gradients

Published online by Cambridge University Press:  15 February 2016

D. Fiscaletti ,
A. Attili ,
F. Bisetti  and
G. E. Elsinga
D. Fiscaletti*
Affiliation:
Laboratory for Aero and Hydrodynamics, Department of Mechanical, Maritime, and Materials Engineering, Delft University of Technology, Leeghwaterstraat 21, 2628 CA, Delft, The Netherlands
A. Attili
Affiliation:
Clean Combustion Research Center, King Abdullah University of Science and Technology, Thuwal 23955, Saudi Arabia
F. Bisetti
Affiliation:
Clean Combustion Research Center, King Abdullah University of Science and Technology, Thuwal 23955, Saudi Arabia
G. E. Elsinga
Affiliation:
Laboratory for Aero and Hydrodynamics, Department of Mechanical, Maritime, and Materials Engineering, Delft University of Technology, Leeghwaterstraat 21, 2628 CA, Delft, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The interaction between the large and the small scales of turbulence is investigated in a mixing layer, at a Reynolds number based on the Taylor microscale (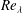$Re_{{\it\lambda}}$) of 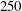$250$, via direct numerical simulations. The analysis is performed in physical space, and the local vorticity root-mean-square (r.m.s.) is taken as a measure of the small-scale activity. It is found that positive large-scale velocity fluctuations correspond to large vorticity r.m.s. on the low-speed side of the mixing layer, whereas, they correspond to low vorticity r.m.s. on the high-speed side. The relationship between large and small scales thus depends on position if the vorticity r.m.s. is correlated with the large-scale velocity fluctuations. On the contrary, the correlation coefficient is nearly constant throughout the mixing layer and close to unity if the vorticity r.m.s. is correlated with the large-scale velocity gradients. Therefore, the small-scale activity appears closely related to large-scale gradients, while the correlation between the small-scale activity and the large-scale velocity fluctuations is shown to reflect a property of the large scales. Furthermore, the vorticity from unfiltered (small scales) and from low pass filtered (large scales) velocity fields tend to be aligned when examined within vortical tubes. These results provide evidence for the so-called ‘scale invariance’ (Meneveau & Katz, Annu. Rev. Fluid Mech., vol. 32, 2000, pp. 1–32), and suggest that some of the large-scale characteristics are not lost at the small scales, at least at the Reynolds number achieved in the present simulation.

JFM classification

Turbulent Flows: Shear layer turbulence Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 791 , 25 March 2016 , pp. 154 - 173
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Attili, A. & Bisetti, F. 2012 Statistics and scaling of turbulence in a spatially developing mixing layer at $Re_{{\it\lambda}}=250$ . Phys. Fluids 24, 035109.CrossRefGoogle Scholar
Attili, A. & Bisetti, F. 2013 Fluctuations of a passive scalar in a turbulent mixing layer. Phys. Rev. E 88 (3), 033013.Google Scholar
Attili, A., Cristancho, J. C. & Bisetti, F. 2014 Statistics of the turbulent/non-turbulent interface in a spatially developing mixing layer. J. Turbul. 15 (9), 555–568.Google Scholar
Bandyopadhyay, P. R. & Hussain, K. M. F. 1984 The coupling between scales in shear flows. Phys. Fluids 27, 2221–2228.CrossRefGoogle Scholar
Batchelor, G. K. & Townsend, A. A. 1949 The nature of turbulent motion at large wave-numbers. Proc. R. Soc. Lond. A 199, 238–255.Google Scholar
Bell, J. & Mehta, R. 1990 Development of a two-stream mixing layer from tripped and untripped boundary layers. AIAA J. 28, 2034–2042.CrossRefGoogle Scholar
Bernardini, M. & Pirozzoli, S. 2011 Inner/outer layer interactions in turbulent boundary layers: A refined measure for the large-scale amplitude modulation mechanism. Phys. Fluids 23, 061701.Google Scholar
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64 (04), 775–816.Google Scholar
Buxton, O. R. H.2011 Fine scale features of turbulent shear flows. PhD thesis, Imperial College London.Google Scholar
Buxton, O. R. H. & Ganapathisubramani, B. 2014 Concurrent scale interactions in the far-field of a turbulent mixing layer. Phys. Fluids 26, 125106.Google Scholar
Buxton, O. R. H., de Kat, R. & Ganapathisubramani, B. 2013 The convection of large and intermediate scale fluctuations in a turbulent mixing layer. Phys. Fluids 25, 125105.Google Scholar
Chung, D. & McKeon, B. J. 2010 Large-eddy simulation of large-scale structures in long channel flow. J. Fluid Mech. 661, 341–364.Google Scholar
Desjardins, O., Blanquart, G., Balarac, G. & Pitsch, H. 2008 High order conservative finite difference scheme for variable density low Mach number turbulent flows. J. Comput. Phys. 227 (15), 7125–7159.Google Scholar
Elsinga, G. E. & Marusic, I. 2010 Universal aspects of small-scale motions in turbulence. J. Fluid Mech. 662, 514–539.Google Scholar
Ferchichi, M. & Tavoularis, S. 2000 Reynolds number effects on the fine structure of uniformly sheared turbulence. Phys. Fluids 12, 2942–2953.Google Scholar
Ferré, J. A., Mumford, J. C., Savill, A. M. & Giralt, F. 1990 Three-dimensional large-eddy motions and fine-scale activity in a plane turbulent wake. J. Fluid Mech. 210, 371–414.Google Scholar
Fiscaletti, D., Ganapathisubramani, B. & Elsinga, G. E. 2015 Amplitude and frequency modulation of the small scales in a jet. J. Fluid Mech. 772, 756–783.Google Scholar
Ganapathisubramani, B., Hutchins, N., Monty, J. P., Chung, D. & Marusic, I. 2012 Amplitude and frequency modulation in wall turbulence. J. Fluid Mech. 712, 61–91.Google Scholar
Germano, M., Piomelli, U., Moin, P. & Cabot, W. H. 1991 A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3, 1760–1765.Google Scholar
Hunt, J. C. R., Eames, I., Westerweel, J., Davidson, P. A., Voropayev, S., Fernando, J. & Braza, M. 2010 Thin shear layers – The key to turbulence structure? J. Hydro. Environ. Res. 4, 75–82.Google Scholar
Hunt, J. C. R., Ishihara, T., Worth, N. A. & Kaneda, T. 2014 Thin shear layer structures in high Reynolds number turbulence. Flow Turbul. Combust. 92, 607–649.Google Scholar
Hutchins, N. & Marusic, I. 2007 Large-scale influences in near-wall turbulence. Phil. Trans. R. Soc. Lond. A 365, 647–664.Google Scholar
Ishihara, T., Kaneda, Y. & Hunt, J. C. R. 2013 Thin shear layers in high Reynolds number turbulence – DNS results. Flow Turbul. Combust. 91, 895–929.Google Scholar
Jiménez, J. 2012 Cascades in wall-bounded turbulence. Annu. Rev. Fluid Mech. 44, 27–45.Google Scholar
Kim, J. & Moin, P. 1985 Application of a fractional-step method to incompressible Navier–Stokes equations. J. Comput. Phys. 59 (2), 308–323.CrossRefGoogle Scholar
Kolmogorov, A. N. 1941a Energy dissipation in locally isotropic turbulence. C. R. Acad. Sci. URSS 32, 16.Google Scholar
Kolmogorov, A. N. 1941b The local structure of turbulence in incompressible viscous fluid for very large Reynolds. C. R. Acad. Sci. URSS 30, 301.Google Scholar
Lilly, D. K. 1967 The representation of small-scale turbulence in numerical simulation experiments. In Proceedings of the IBM Scientific Computing Symposium on Environmental Science, Yorktown Heights, New York, p. 195.Google Scholar
Marusic, I., Mathis, R. & Hutchins, N. 2010 Predictive model for wall-bounded turbulent flow. Science 329, 193–196.Google Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2009a Large-scale amplitude modulation of the small-scale structures in turbulent boundary layers. J. Fluid Mech. 628, 311–337.CrossRefGoogle Scholar
Mathis, R., Hutchins, N. & Marusic, I. 2011 A predictive inner–outer model for streamwise turbulence statistics in wall-bounded flows. J. Fluid Mech. 681, 537–566.CrossRefGoogle Scholar
Mathis, R., Monty, J., Hutchins, N. & Marusic, I. 2009b Comparison of large-scale amplitude modulation in turbulent boundary layers, pipes and channel flows. Phys. Fluids 21, 111703.Google Scholar
Meneveau, C. & Katz, J. 2000 Scale-invariance and turbulence models for large-eddy simulation. Annu. Rev. Fluid Mech. 32, 1–32.Google Scholar
Ol’Shanskii, M. A. & Staroverov, V. M. 2000 On simulation of outflow boundary conditions in finite difference calculations for incompressible fluid. Intl J. Numer. Meth. Fluids 33 (4), 499–534.3.0.CO;2-7>CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rogers, M. M. & Moser, R. D. 1994 Direct simulation of a self-similar turbulent mixing layer. Phys. Fluids 6, 903.CrossRefGoogle Scholar
Schlatter, P. & Örlü, R. 2010 Quantifying the interaction between large and small scales in wall-bounded turbulent flows: A note of caution. Phys. Fluids 22, 051704.Google Scholar
Shen, X. & Warhaft, Z. 2000 The anisotropy of the small scale structure in high Reynolds number ( $R_{{\it\lambda}}$ ${\sim}1000$ ) turbulent shear flow. Phys. Fluids 12, 2976–2989.Google Scholar
Smagorinsky, J. 1963 General circulation experiments with the primitive equations. I. The basic experiment. Mon. Weath. Rev. 91, 99–164.Google Scholar
Vernet, A., Kopp, G. A., Ferré, J. A. & Giralt, F. 1999 Three-dimensional structure and momentum transfer in a turbulent cylinder wake. J. Fluid Mech. 210, 303–337.Google Scholar
Worth, N. A. & Nickels, T. B. 2011 Some characteristics of thin shear layers in homogeneous turbulent flow. Phil. Trans. R. Soc. Lond. A 369, 709–722.Google Scholar
Yeung, P. K., Brasseur, J. G. & Wang, Q. 1995 Dynamics of direct large-small scale couplings in coherently forced turbulence: concurrent physical- and Fourier-space views. J. Fluid Mech. 283, 43–95.CrossRefGoogle Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.Google Scholar