Published online by Cambridge University Press: 28 March 2017
A semi-empirical model is presented that describes the development of a fully developed turbulent boundary layer in the presence of surface roughness with length scale  $k_{s}$ that varies with streamwise distance
$k_{s}$ that varies with streamwise distance  $x$. Interest is centred on flows for which all terms of the von Kármán integral relation, including the ratio of outer velocity to friction velocity
$x$. Interest is centred on flows for which all terms of the von Kármán integral relation, including the ratio of outer velocity to friction velocity 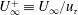 $U_{\infty }^{+}\equiv U_{\infty }/u_{\unicode[STIX]{x1D70F}}$, are streamwise constant. For
$U_{\infty }^{+}\equiv U_{\infty }/u_{\unicode[STIX]{x1D70F}}$, are streamwise constant. For 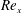 $Re_{x}$ assumed large, use is made of a simple log-wake model of the local turbulent mean-velocity profile that contains a standard mean-velocity correction for the asymptotic fully rough regime and with assumed constant parameter values. It is then shown that, for a general power-law external velocity variation
$Re_{x}$ assumed large, use is made of a simple log-wake model of the local turbulent mean-velocity profile that contains a standard mean-velocity correction for the asymptotic fully rough regime and with assumed constant parameter values. It is then shown that, for a general power-law external velocity variation 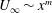 $U_{\infty }\sim x^{m}$, all measures of the boundary-layer thickness must be proportional to
$U_{\infty }\sim x^{m}$, all measures of the boundary-layer thickness must be proportional to  $x$ and that the surface sand-grain roughness scale variation must be the linear form
$x$ and that the surface sand-grain roughness scale variation must be the linear form 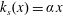 $k_{s}(x)=\unicode[STIX]{x1D6FC}x$, where
$k_{s}(x)=\unicode[STIX]{x1D6FC}x$, where  $x$ is the distance from the boundary layer of zero thickness and
$x$ is the distance from the boundary layer of zero thickness and  $\unicode[STIX]{x1D6FC}$ is a dimensionless constant. This is shown to give a two-parameter
$\unicode[STIX]{x1D6FC}$ is a dimensionless constant. This is shown to give a two-parameter 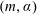 $(m,\unicode[STIX]{x1D6FC})$ family of solutions, for which
$(m,\unicode[STIX]{x1D6FC})$ family of solutions, for which 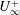 $U_{\infty }^{+}$ (or equivalently
$U_{\infty }^{+}$ (or equivalently 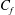 $C_{f}$) and boundary-layer thicknesses can be simply calculated. These correspond to perfectly self-similar boundary-layer growth in the streamwise direction with similarity variable
$C_{f}$) and boundary-layer thicknesses can be simply calculated. These correspond to perfectly self-similar boundary-layer growth in the streamwise direction with similarity variable 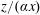 $z/(\unicode[STIX]{x1D6FC}x)$, where
$z/(\unicode[STIX]{x1D6FC}x)$, where  $z$ is the wall-normal coordinate. Results from this model over a range of
$z$ is the wall-normal coordinate. Results from this model over a range of  $\unicode[STIX]{x1D6FC}$ are discussed for several cases, including the zero-pressure-gradient (
$\unicode[STIX]{x1D6FC}$ are discussed for several cases, including the zero-pressure-gradient (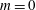 $m=0$) and sink-flow (
$m=0$) and sink-flow (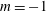 $m=-1$) boundary layers. Trends observed in the model are supported by wall-modelled large-eddy simulation of the zero-pressure-gradient case for
$m=-1$) boundary layers. Trends observed in the model are supported by wall-modelled large-eddy simulation of the zero-pressure-gradient case for 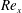 $Re_{x}$ in the range
$Re_{x}$ in the range 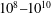 $10^{8}{-}10^{10}$ and for four values of
$10^{8}{-}10^{10}$ and for four values of  $\unicode[STIX]{x1D6FC}$. Linear streamwise growth of the displacement, momentum and nominal boundary-layer thicknesses is confirmed, while, for each
$\unicode[STIX]{x1D6FC}$. Linear streamwise growth of the displacement, momentum and nominal boundary-layer thicknesses is confirmed, while, for each  $\unicode[STIX]{x1D6FC}$, the mean-velocity profiles and streamwise turbulent variances are found to collapse reasonably well onto
$\unicode[STIX]{x1D6FC}$, the mean-velocity profiles and streamwise turbulent variances are found to collapse reasonably well onto 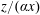 $z/(\unicode[STIX]{x1D6FC}x)$. For given
$z/(\unicode[STIX]{x1D6FC}x)$. For given  $\unicode[STIX]{x1D6FC}$, calculations of
$\unicode[STIX]{x1D6FC}$, calculations of 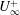 $U_{\infty }^{+}$ obtained from large-eddy simulations are streamwise constant and independent of
$U_{\infty }^{+}$ obtained from large-eddy simulations are streamwise constant and independent of 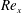 $Re_{x}$ when this is large. The present results suggest that, in the sense that
$Re_{x}$ when this is large. The present results suggest that, in the sense that 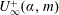 $U_{\infty }^{+}(\unicode[STIX]{x1D6FC},m)$ is constant, these flows can be interpreted as the fully rough limit for boundary layers in the presence of small-scale linear roughness.
$U_{\infty }^{+}(\unicode[STIX]{x1D6FC},m)$ is constant, these flows can be interpreted as the fully rough limit for boundary layers in the presence of small-scale linear roughness.
Present address: Mechanical Engineering, Physical Sciences and Engineering Division, King Abdullah University of Science and Technology, Thuwal, Saudi Arabia, 23955-6900.