Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kim, Hyoungsoo
Belmiloud, Naser
and
Mertens, Paul W.
2016.
Tomographic PIV measurement of internal complex flow of an evaporating droplet with non-uniformly receding contact lines.
Journal of the Korean Society of Visualization,
Vol. 14,
Issue. 2,
p.
31.
Song, Yuting
Lu, Ziyang
Yang, Haijun
Zhang, Suojiang
and
Zhang, Xuehua
2016.
Dissolution of Sessile Microdroplets of Electrolyte and Graphene Oxide Solutions in an Ouzo System.
Langmuir,
Vol. 32,
Issue. 40,
p.
10296.
Laghezza, Gianluca
Dietrich, Erik
Yeomans, Julia M.
Ledesma-Aguilar, Rodrigo
Kooij, E. Stefan
Zandvliet, Harold J. W.
and
Lohse, Detlef
2016.
Collective and convective effects compete in patterns of dissolving surface droplets.
Soft Matter,
Vol. 12,
Issue. 26,
p.
5787.
Maheshwari, Shantanu
van der Hoef, Martin
Zhang, Xuehua
and
Lohse, Detlef
2016.
Stability of Surface Nanobubbles: A Molecular Dynamics Study.
Langmuir,
Vol. 32,
Issue. 43,
p.
11116.
Diddens, Christian
Tan, Huanshu
Lv, Pengyu
Versluis, Michel
Kuerten, J. G. M.
Zhang, Xuehua
and
Lohse, Detlef
2017.
Evaporating pure, binary and ternary droplets: thermal effects and axial symmetry breaking.
Journal of Fluid Mechanics,
Vol. 823,
Issue. ,
p.
470.
Dietrich, Erik
Rump, Maaike
Lv, Pengyu
Kooij, E. Stefan
Zandvliet, Harold J. W.
and
Lohse, Detlef
2017.
Segregation in dissolving binary-component sessile droplets.
Journal of Fluid Mechanics,
Vol. 812,
Issue. ,
p.
349.
Duplat, Jerome
Grandemange, Mathieu
and
Poulain, Cedric
2017.
Convective mass transfer around a dissolving bubble.
Physical Review Fluids,
Vol. 2,
Issue. 11,
Peñas-López, Pablo
Moreno Soto, Álvaro
Parrales, Miguel A.
van der Meer, Devaraj
Lohse, Detlef
and
Rodríguez-Rodríguez, Javier
2017.
The history effect on bubble growth and dissolution. Part 2. Experiments and simulations of a spherical bubble attached to a horizontal flat plate.
Journal of Fluid Mechanics,
Vol. 820,
Issue. ,
p.
479.
Dollet, Benjamin
and
Boulogne, François
2017.
Natural convection above circular disks of evaporating liquids.
Physical Review Fluids,
Vol. 2,
Issue. 5,
Moreno Soto, Álvaro
Prosperetti, Andrea
Lohse, Detlef
and
van der Meer, Devaraj
2017.
Gas depletion through single gas bubble diffusive growth and its effect on subsequent bubbles.
Journal of Fluid Mechanics,
Vol. 831,
Issue. ,
p.
474.
Misyura, S. Y.
2017.
Evaporation of a sessile water drop and a drop of aqueous salt solution.
Scientific Reports,
Vol. 7,
Issue. 1,
Jativa, Fernando
and
Zhang, Xuehua
2017.
Transparent Silk Fibroin Microspheres from Controlled Droplet Dissolution in a Binary Solution.
Langmuir,
Vol. 33,
Issue. 31,
p.
7780.
Maheshwari, Shantanu
van der Hoef, Martin
Prosperetti, Andrea
and
Lohse, Detlef
2017.
Molecular dynamics study of multicomponent droplet dissolution in a sparingly miscible liquid.
Journal of Fluid Mechanics,
Vol. 833,
Issue. ,
p.
54.
Lu, Ziyang
Rezk, Amgad
Jativa, Fernando
Yeo, Leslie
and
Zhang, Xuehua
2017.
Dissolution dynamics of a suspension droplet in a binary solution for controlled nanoparticle assembly.
Nanoscale,
Vol. 9,
Issue. 36,
p.
13441.
Schweigler, K.M.
Ben Said, M.
Seifritz, S.
Selzer, M.
and
Nestler, B.
2017.
Experimental and numerical investigation of drop evaporation depending on the shape of the liquid/gas interface.
International Journal of Heat and Mass Transfer,
Vol. 105,
Issue. ,
p.
655.
Boulogne, François
and
Dollet, Benjamin
2018.
Convective evaporation of vertical films.
Soft Matter,
Vol. 14,
Issue. 9,
p.
1665.
Li, Yaxing
Lv, Pengyu
Diddens, Christian
Tan, Huanshu
Wijshoff, Herman
Versluis, Michel
and
Lohse, Detlef
2018.
Evaporation-Triggered Segregation of Sessile Binary Droplets.
Physical Review Letters,
Vol. 120,
Issue. 22,
Bao, Lei
Spandan, Vamsi
Yang, Yantao
Dyett, Brendan
Verzicco, Roberto
Lohse, Detlef
and
Zhang, Xuehua
2018.
Flow-induced dissolution of femtoliter surface droplet arrays.
Lab on a Chip,
Vol. 18,
Issue. 7,
p.
1066.
Maheshwari, Shantanu
van der Hoef, Martin
Rodrı́guez Rodrı́guez, Javier
and
Lohse, Detlef
2018.
Leakiness of Pinned Neighboring Surface Nanobubbles Induced by Strong Gas–Surface Interaction.
ACS Nano,
Vol. 12,
Issue. 3,
p.
2603.
Tan, Huanshu
Diddens, Christian
Mohammed, Ali Akash
Li, Junyi
Versluis, Michel
Zhang, Xuehua
and
Lohse, Detlef
2019.
Microdroplet nucleation by dissolution of a multicomponent drop in a host liquid.
Journal of Fluid Mechanics,
Vol. 870,
Issue. ,
p.
217.
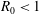 $R_{0}<1$ mm) long-chain alcohol (of various types) sessile droplets in water is studied, disentangling diffusive and convective contributions. The latter can arise for high solubilities of the alcohol, as the density of the alcohol–water mixture is then considerably less than that of pure water, giving rise to buoyancy-driven convection. The convective flow around the droplets is measured, using micro-particle image velocimetry (
$R_{0}<1$ mm) long-chain alcohol (of various types) sessile droplets in water is studied, disentangling diffusive and convective contributions. The latter can arise for high solubilities of the alcohol, as the density of the alcohol–water mixture is then considerably less than that of pure water, giving rise to buoyancy-driven convection. The convective flow around the droplets is measured, using micro-particle image velocimetry (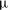 ${\rm\mu}$PIV) and the schlieren technique. When non-dimensionalizing the system, we find a universal
${\rm\mu}$PIV) and the schlieren technique. When non-dimensionalizing the system, we find a universal  $Sh\sim Ra^{1/4}$ scaling relation for all alcohols (of different solubilities) and all droplets in the convective regime. Here
$Sh\sim Ra^{1/4}$ scaling relation for all alcohols (of different solubilities) and all droplets in the convective regime. Here 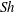 $Sh$ is the Sherwood number (dimensionless mass flux) and
$Sh$ is the Sherwood number (dimensionless mass flux) and 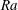 $Ra$ is the Rayleigh number (dimensionless density difference between clean and alcohol-saturated water). This scaling implies the scaling relation
$Ra$ is the Rayleigh number (dimensionless density difference between clean and alcohol-saturated water). This scaling implies the scaling relation 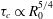 ${\it\tau}_{c}\propto R_{0}^{5/4}$ of the convective dissolution time
${\it\tau}_{c}\propto R_{0}^{5/4}$ of the convective dissolution time 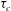 ${\it\tau}_{c}$, which is found to agree with experimental data. We show that in the convective regime the plume Reynolds number (the dimensionless velocity) of the detaching alcohol-saturated plume follows
${\it\tau}_{c}$, which is found to agree with experimental data. We show that in the convective regime the plume Reynolds number (the dimensionless velocity) of the detaching alcohol-saturated plume follows 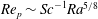 $Re_{p}\sim Sc^{-1}Ra^{5/8}$, which is confirmed by the
$Re_{p}\sim Sc^{-1}Ra^{5/8}$, which is confirmed by the 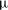 ${\rm\mu}$PIV data. Here,
${\rm\mu}$PIV data. Here, 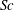 $Sc$ is the Schmidt number. The convective regime exists when
$Sc$ is the Schmidt number. The convective regime exists when 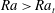 $Ra>Ra_{t}$, where
$Ra>Ra_{t}$, where  $Ra_{t}=12$ is the transition
$Ra_{t}=12$ is the transition 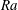 $Ra$ number as extracted from the data. For
$Ra$ number as extracted from the data. For 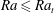 $Ra\leqslant Ra_{t}$ and smaller, convective transport is progressively overtaken by diffusion and the above scaling relations break down.
$Ra\leqslant Ra_{t}$ and smaller, convective transport is progressively overtaken by diffusion and the above scaling relations break down.