Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T15:17:26.011Z Has data issue: false hasContentIssue false
  • English
  • Français

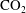Rock dissolution patterns and geochemical shutdown of $\text{CO}_{2}$–brine–carbonate reactions during convective mixing in porous media

Published online by Cambridge University Press:  05 January 2015

X. Fu ,
L. Cueto-Felgueroso ,
D. Bolster  and
R. Juanes
X. Fu
Affiliation:
Department of Civil & Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
L. Cueto-Felgueroso
Affiliation:
Department of Civil & Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA Civil Engineering School, Technical University of Madrid, Madrid, Spain
D. Bolster
Affiliation:
Department of Civil and Environmental Engineering and Earth Sciences, University of Notre Dame, Notre Dame, IN 46556, USA
R. Juanes*
Affiliation:
Department of Civil & Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

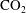Motivated by the process of $\text{CO}_{2}$ convective mixing in porous media, here we study the formation of rock-dissolution patterns that arise from geochemical reactions during Rayleigh–Bénard–Darcy convection. Under the assumption of instantaneous chemical equilibrium, we adopt a formulation of the local reaction rate as a function of scalar dissipation rate, a measure that depends solely on flow and transport, and chemical speciation, which is a measure that depends only on the equilibrium thermodynamics of the chemical system. We use high-resolution simulations to examine the interplay between the density-driven hydrodynamic instability and the rock dissolution reactions, and analyse the impact of geochemical reactions on the macroscopic mass exchange rate. We find that dissolution of carbonate rock initiates in regions of locally high mixing, but that the geochemical reaction shuts down significantly earlier than shutdown of convective mixing. This early shutdown feature reflects the important role that chemical speciation plays in this hydrodynamics–reaction coupled process. Finally, we extend our analysis to three dimensions and explore the morphology of dissolution patterns in three dimensions.

JFM classification

Low-Reynolds-number flows: Porous media
Type
Papers
Information
Journal of Fluid Mechanics , Volume 764 , 10 February 2015 , pp. 296 - 315
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andre, B. J. & Rajaram, H. 2005 Dissolution of limestone fractures by cooling waters: early development of hypogene karst systems. Water Resour. Res. 41 (1), W01015.Google Scholar
Backhaus, S., Turitsyn, K. & Ecke, R. E. 2011 Convective instability and mass transport of diffusion layers in a Hele-Shaw geometry. Phys. Rev. Lett. 106 (10), 104501.Google Scholar
Bolster, D. 2014 The fluid mechanics of dissolution trapping in geologic storage of $\text{CO}_{2}$ . J. Fluid Mech. 740, 1–4.Google Scholar
Carroll, S., Hao, Y., Smith, M. & Sholokhova, Y. 2013 Development of scaling parameters to describe $\text{CO}_{2}$ –rock interactions within Weyburn–Midale carbonate flow units. Intl J. Greenh. Gas Control 16, S185–S193.Google Scholar
De Simoni, M., Carrera, J., Sánchez-Vila, X. & Guadagnini, A. 2005 A procedure for the solution of multicomponent reactive transport problems. Water Resour. Res. 41 (11), W11410.Google Scholar
De Simoni, M., Sánchez-Vila, X., Carrera, J. & Saaltink, M. W. 2007 A mixing ratios-based formulation for multicomponent reactive transport. Water Resour. Res. 43 (7), W07419.CrossRefGoogle Scholar
Detwiler, R. L. & Rajaram, H. 2007 Predicting dissolution patterns in variable aperture fractures: evaluation of an enhanced depth-averaged computational model. Water Resour. Res. 43 (4), W04403.Google Scholar
Elkhoury, J. E., Ameli, P. & Detwiler, R. L. 2013 Dissolution and deformation in fractured carbonates caused by flow of $\text{CO}_{2}$ -rich brine under reservoir conditions. Intl J. Greenh. Gas Control 16, S203–S215.Google Scholar
Ennis-King, J. & Paterson, L. 2005 Role of convective mixing in the long-term storage of carbon dioxide in deep saline formations. Soc. Petrol. Engng J. 10 (3), 349–356.Google Scholar
Fu, X., Cueto-Felgueroso, L. & Juanes, R. 2013 Pattern formation and coarsening dynamics in three-dimensional convective mixing in porous media. Phil. Trans. R. Soc. A 371, 20120355.Google Scholar
Guadagnini, A., Sanchez-Vila, X., Saaltink, M. W., Bussini, M. & Berkowitz, B. 2009 Application of a mixing-ratios based formulation to model mixing-driven dissolution experiments. Adv. Water Resour. 32 (5), 756–766.CrossRefGoogle Scholar
Hammond, G. E., Lichtner, P. C., Lu, C. & Mills, R. T. 2012 PFLOTRAN: reactive flow and transport code for use on laptops to leadership-class supercomputers. In Groundwater Reactive Transport Models (ed. Zhang, F., Yeh, G. T. & Parker, J. C.), pp. 141–159. Bentham Science Publishers.Google Scholar
Hassanzadeh, H., Pooladi-Darvish, M. & Keith, D. W. 2007 Scaling behavior of convective mixing, with application to geological storage of $\text{CO}_{2}$ . AIChE J. 53 (5), 1121–1131.Google Scholar
Helgerson, H. C. & Kirkham, D. H. 1974 Theoretical prediction of the thermodynamic behaviour of aqueous electrolytes at high pressure and temperature: II Debye–Hückel parameters for activity coefficients and relative partial molol properties. Am. J. Sci. 274, 1199–1261.Google Scholar
Hewitt, D. R., Neufeld, J. A. & Lister, J. R. 2013 Convective shutdown in a porous medium at high Rayleigh number. J. Fluid Mech. 719, 551–586.CrossRefGoogle Scholar
Hidalgo, J. J. & Carrera, J. 2009 Effect of dispersion on the onset of convection during $\text{CO}_{2}$ sequestration. J. Fluid Mech. 640, 441–452.Google Scholar
Hidalgo, J. J., Fe, J., Cueto-Felgueroso, L. & Juanes, R. 2012 Scaling of convective mixing in porous media. Phys. Rev. Lett. 109, 264503.Google Scholar
IPCC 2005 Special Report on Carbon Dioxide Capture and Storage (ed. Metz, B. et al. ), Cambridge University Press.Google Scholar
Kneafsey, T. J. & Pruess, K. 2010 Laboratory flow experiments for visualizing carbon dioxide-induced, density-driven brine convection. Transp. Porous Med. 82, 123–139.CrossRefGoogle Scholar
Lackner, K. S. 2003 A guide to $\text{CO}_{2}$ sequestration. Science 300 (5626), 1677–1678.Google Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.Google Scholar
Lichtner, P. C. 1996 Continuum formulation of multicomponent-multiphase reactive transport. In Reactive Transport in Porous Media (ed. Lichtner, P. C., Steefel, C. I. & Oelkers, E. H.), Reviews in Mineralogy, vol. 34, chap. 1, pp. 1–81. Mineralogical Society of America.Google Scholar
Lindeberg, E. & Wessel-Berg, D. 1997 Vertical convection in an aquifer column under a gas cap of $\text{CO}_{2}$ . Energy Convers. Manage. 38, S229–S234.Google Scholar
MacMinn, C. W. & Juanes, R. 2013 Buoyant currents arrested by convective dissolution. Geophys. Res. Lett. 40, 2017–2022.Google Scholar
MacMinn, C. W., Neufeld, J. A., Hesse, M. A. & Huppert, H. E. 2012 Spreading and convective dissolution of carbon dioxide in vertically confined, horizontal aquifers. Water Resour. Res. 48, W11516.Google Scholar
MacMinn, C. W., Szulczewski, M. L. & Juanes, R. 2011 $\text{CO}_{2}$ migration in saline aquifers. Part 2: capillary and solubility trapping. J. Fluid Mech. 688, 321–351.Google Scholar
Neufeld, J. A., Hesse, M. A., Riaz, A., Hallworth, M. A., Tchelepi, H. A. & Huppert, H. E. 2010 Convective dissolution of carbon dioxide in saline aquifers. Geophys. Res. Lett. 37, L22404.Google Scholar
Nield, D. A. & Bejan, A. 2006 Convection in Porous Media, 3rd edn. Springer.Google Scholar
Olivella, S., Gens, A., Carrera, J. & Alonso, E. E. 1996 Numerical formulation for a simulator (code_bright) for the coupled analysis of saline media. Engng Comput. 13 (7), 87–112.Google Scholar
Orr, F. M. Jr. 2009 Onshore geologic storage of $\text{CO}_{2}$ . Science 325, 1656–1658.Google Scholar
Parkhurst, D. L.1995 User’s guide to PHREEQC: a computer program for speciation, reaction-path, advective-transport, and inverse geochemical calculations, Water Resources Investigations Report. Lakewood, Colorado.Google Scholar
Pau, G. S. H., Bell, J. B., Pruess, K., Almgren, A. S., Lijewski, M. J. & Zhang, K. 2010 High-resolution simulation and characterization of density-driven flow in $\text{CO}_{2}$ storage in saline aquifers. Adv. Water Resour. 33 (4), 443–455.CrossRefGoogle Scholar
Plummer, L. N., Wigley, T. M. L. & Parkhurst, D. L. 1978 The kinetics of calcite dissolution in $\text{CO}_{2}$ –water systems at $5^{\circ }$ to $60\,^{\circ }\text{C}$ and 0.0 to 1.0 atm $\text{CO}_{2}$ . Am. J. Sci. 278, 179–216.CrossRefGoogle Scholar
Rezaei, M., Sanz, E., Raeisi, E., Ayora, C., Vázquez-Suñé, E. & Carrera, J. 2005 Reactive transport modeling of calcite dissolution in the fresh–salt water mixing zone. J. Hydrol. 311, 282–298.Google Scholar
Riaz, A., Hesse, M., Tchelepi, H. A. & Orr, F. M. Jr. 2006 Onset of convection in a gravitationally unstable, diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111.Google Scholar
Riaz, A. & Meiburg, E. 2003 Three-dimensional miscible displacement simulations in homogeneous porous media with gravity override. J. Fluid Mech. 494, 95–117.Google Scholar
Romanov, D. & Dreybrodt, W. 2006 Evolution of porosity in the saltwater–freshwater mixing zone of coastal carbonate aquifers: an alternative modelling approach. J. Hydrol. 329, 661–673.Google Scholar
Ruith, M. & Meiburg, E. 2000 Miscible rectilinear displacements with gravity override. Part 1. Homogeneous porous medium. J. Fluid Mech. 420, 225–257.Google Scholar
Saaltink, M. W., Ayora, C. & Carrera, J. 1998 A mathematical formulation for reactive transport that eliminates mineral concentrations. Water Resour. Res. 34 (7), 1649–1656.Google Scholar
Saaltink, M. W., Batlle, F., Ayora, C., Carrera, J. & Olivella, S. 2004 RETRASO, a code for modeling reactive transport in saturated and unsaturated porous media. Geol. Acta 2 (3), 235–251.Google Scholar
Saaltink, M. W., Vilarrasa, V., De Gaspari, F., Silva, O., Carrera, J. & Rötting, T. S. 2013 A method for incorporating equilibrium chemical reactions into multiphase flow models for $\text{CO}_{2}$ storage. Adv. Water Resour. 62, 431–441.Google Scholar
Sanchez-Vila, X., Dentz, M. & Donado, L. D. 2007 Transport-controlled reaction rates under local non-equilibrium conditions. Geophys. Res. Lett. 34 (10), L10404.Google Scholar
Sanford, W. E. & Konikow, L. F. 1989 Simulation of calcite dissolution and porosity changes in saltwater mixing zones in coastal aquifers. Water Resour. Res. 25 (4), 655–667.CrossRefGoogle Scholar
Slim, A. 2014 Solutal–convection regimes in a two-dimensional porous medium. J. Fluid Mech. 741, 461–491.Google Scholar
Slim, A., Bandi, M. M., Miller, J. C. & Mahadevan, L. 2013 Dissolution-driven convection in a Hele-Shaw cell. Phys. Fluids 25, 024101.Google Scholar
Steefel, C. I. & Lasaga, A. C. 1994 A coupled model for transport of multiple chemical species and kinetic precipitation/dissolution reactions with application to reactive flow in single phase hydrothermal systems. Am. J. Sci. 294 (5), 529–592.CrossRefGoogle Scholar
Steefel, C. I. & MacQuarrie, K. T. B. 1996 Approaches to modeling of reactive transport in porous media. In Reactive Transport in Porous Media (ed. Lichtner, P. C., Steefel, C. I. & Oelkers, E. H.), Reviews in Mineralogy, vol. 34, chap. 2, pp. 83–129. Mineralogical Society of America.Google Scholar
Swarztrauber, P. N. 1977 The methods of cyclic reduction, Fourier analysis, and the FACR algorithm for the discrete solution of Poisson’s equation on a rectangle. SIAM Rev. 19, 490–501.Google Scholar
Szulczewski, M. L., Hesse, M. A. & Juanes, R. 2013 The evolution of miscible gravity currents in horizontal porous layers. J. Fluid Mech. 736, 287–315.CrossRefGoogle Scholar
Szulczewski, M. L., MacMinn, C. W., Herzog, H. J. & Juanes, R. 2012 Lifetime of carbon capture and storage as a climate-change mitigation technology. Proc. Natl Acad. Sci. USA 109 (14), 5185–5189.Google Scholar
Szymczak, P. & Ladd, A. J. C. 2011 The initial stages of cave formation: beyond the one-dimensional paradigm. Earth Planet. Sci. Lett. 301 (3–4), 424–432.Google Scholar
Tan, C. T. & Homsy, G. M. 1988 Simulation of nonlinear viscous fingering in miscible displacement. Phys. Fluids 6, 1330–1338.Google Scholar
Weir, G. J., White, S. P. & Kissling, W. M. 1996 Reservoir storage and containment of greenhouse gases. Transp. Porous Med. 23 (1), 37–60.Google Scholar
Xu, T. F., Apps, J. A. & Pruess, K. 2003 Reactive geochemical transport simulation to study mineral trapping for $\text{CO}_{2}$ disposal in deep arenaceous formations. J. Geophys. Res. 108 (B2), 2071.Google Scholar
Xu, T., Kharaka, Y. K., Doughty, C., Freifeld, B. M. & Daley, T. M. 2010 Reactive transport modeling to study changes in water chemistry induced by $\text{CO}_{2}$ injection at the Frio-I Brine Pilot. Chem. Geol. 271 (3–4), 153–164.Google Scholar
Xu, T., Sonnenthal, E., Spycher, N. & Pruess, K. 2006 TOUGHREACT—a simulation program for non-isothermal multiphase reactive geochemical transport in variably saturated geologic media: applications to geothermal injectivity and $\text{CO}_{2}$ geological sequestration. Comput. Geosci. 32 (2), 145–165.CrossRefGoogle Scholar
Yeh, G. T. & Tripathi, V. S. 1991 A model for simulating transport of reactive multispecies components: model development and demonstration. Water Resour. Res. 27 (12), 3075–3094.Google Scholar