Published online by Cambridge University Press: 13 June 2019
Experiments on Richtmyer–Meshkov instability of quasi-single-mode interfaces are performed. Four quasi-single-mode air/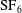 $\text{SF}_{6}$ interfaces with different deviations from the single-mode one are generated by the soap film technique to evaluate the effects of high-order modes on amplitude growth in the linear and weakly nonlinear stages. For each case, two different initial amplitudes are considered to highlight the high-amplitude effect. For the single-mode and saw-tooth interfaces with high initial amplitude, a cavity is observed at the spike head, providing experimental evidence for the previous numerical results for the first time. For the quasi-single-mode interfaces, the fundamental mode is the dominant one such that it determines the amplitude linear growth, and subsequently the impulsive theory gives a reasonable prediction of the experiments by introducing a reduction factor. The discrepancy in linear growth rates between the experiment and the prediction is amplified as the quasi-single-mode interface deviates more severely from the single-mode one. In the weakly nonlinear stage, the nonlinear model valid for a single-mode interface with small amplitude loses efficacy, which indicates that the effects of high-order modes on amplitude growth must be considered. For the saw-tooth interface with small amplitude, the amplitudes of the first three harmonics are extracted from the experiment and compared with the previous theory. The comparison proves that each initial mode develops independently in the linear and weakly nonlinear stages. A nonlinear model proposed by Zhang & Guo (J. Fluid Mech., vol. 786, 2016, pp. 47–61) is then modified by considering the effects of high-order modes. The modified model is proved to be valid in the weakly nonlinear stage even for the cases with high initial amplitude. More high-order modes are needed to match the experiment for the interfaces with a more severe deviation from the single-mode one.
$\text{SF}_{6}$ interfaces with different deviations from the single-mode one are generated by the soap film technique to evaluate the effects of high-order modes on amplitude growth in the linear and weakly nonlinear stages. For each case, two different initial amplitudes are considered to highlight the high-amplitude effect. For the single-mode and saw-tooth interfaces with high initial amplitude, a cavity is observed at the spike head, providing experimental evidence for the previous numerical results for the first time. For the quasi-single-mode interfaces, the fundamental mode is the dominant one such that it determines the amplitude linear growth, and subsequently the impulsive theory gives a reasonable prediction of the experiments by introducing a reduction factor. The discrepancy in linear growth rates between the experiment and the prediction is amplified as the quasi-single-mode interface deviates more severely from the single-mode one. In the weakly nonlinear stage, the nonlinear model valid for a single-mode interface with small amplitude loses efficacy, which indicates that the effects of high-order modes on amplitude growth must be considered. For the saw-tooth interface with small amplitude, the amplitudes of the first three harmonics are extracted from the experiment and compared with the previous theory. The comparison proves that each initial mode develops independently in the linear and weakly nonlinear stages. A nonlinear model proposed by Zhang & Guo (J. Fluid Mech., vol. 786, 2016, pp. 47–61) is then modified by considering the effects of high-order modes. The modified model is proved to be valid in the weakly nonlinear stage even for the cases with high initial amplitude. More high-order modes are needed to match the experiment for the interfaces with a more severe deviation from the single-mode one.