Article contents
Reynolds number scaling of burning rates in spherical turbulent premixed flames
Published online by Cambridge University Press: 05 November 2020
Abstract
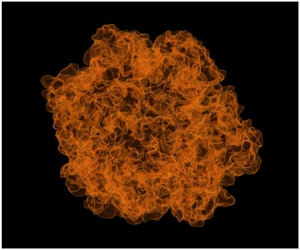
In the flamelet regime of turbulent premixed combustion the enhancement in the burning rates originates primarily from surface wrinkling. In this work we investigate the Reynolds number dependence of burning rates of spherical turbulent premixed methane/air flames in decaying isotropic turbulence with direct numerical simulations. Several simulations are performed by varying the Reynolds number, while keeping the Karlovitz number the same, and the temporal evolution of the flame surface is compared across cases by combining the probability density function of the radial distance of the flame surface from the origin with the surface density function formalism. Because the mean area of the wrinkled flame surface normalized by the area of a sphere with radius equal to the mean flame radius is proportional to the product of the turbulent flame brush thickness and peak surface density within the brush, the temporal evolution of the brush and peak surface density are investigated separately. The brush thickness is shown to scale with the integral scale of the flow, evolving due to decaying velocity fluctuations and stretch. When normalized by the integral scale, the wrinkling scale defined as the inverse of the peak surface density is shown to scale with Reynolds number across simulations and as turbulence decays. As a result, the area ratio and the burning rate are found to increase as  ${Re}_{\lambda }^{1.13}$, in agreement with recent experiments on spherical turbulent premixed flames. We observe that the area ratio does not vary with turbulent intensity when holding the Reynolds number constant.
${Re}_{\lambda }^{1.13}$, in agreement with recent experiments on spherical turbulent premixed flames. We observe that the area ratio does not vary with turbulent intensity when holding the Reynolds number constant.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
REFERENCES
Kulkarni et al. supplementary movie 1
Volume rendering of the outwardly propagating flame front for the simulation R1 (blue colour), along with a planar cut showing the normalized velocity magnitude │V│/SL (white - yellow - red colours).
- 16
- Cited by



