Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T13:36:47.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Reynolds number effect on the velocity derivative flatness factor

Published online by Cambridge University Press:  04 October 2018

M. Meldi Open the ORCID record for M. Meldi [Opens in a new window] ,
L. Djenidi Open the ORCID record for L. Djenidi [Opens in a new window]  and
R. Antonia
M. Meldi*
Affiliation:
Institut PPRIME, Department of Fluid Flow, Heat Transfer and Combustion, CNRS - ENSMA - Université de Poitiers, UPR 3346, SP2MI - Téléport, 211 Bd. Marie et Pierre Curie, B.P. 30179 F86962 Futuroscope Chasseneuil CEDEX, France Aix-Marseille Univ., CNRS, Centrale Marseille, M2P2 Marseille, France
L. Djenidi
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
R. Antonia
Affiliation:
Discipline of Mechanical Engineering, School of Engineering, University of Newcastle, Newcastle, 2308 NSW, Australia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper investigates the effect of a finite Reynolds number (FRN) on the flatness factor (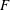$F$) of the velocity derivative in decaying homogeneous isotropic turbulence by applying the eddy damped quasi-normal Markovian (EDQNM) method to calculate all terms in an analytic expression for 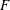$F$ (Djenidi et al., Phys. Fluids, vol. 29 (5), 2017b, 051702). These terms and hence 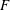$F$ become constant when the Taylor microscale Reynolds number, 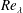$Re_{\unicode[STIX]{x1D706}}$ exceeds approximately 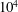$10^{4}$. For smaller values of 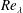$Re_{\unicode[STIX]{x1D706}}$, 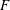$F$, like the skewness 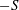$-S$, increases with 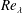$Re_{\unicode[STIX]{x1D706}}$; this behaviour is in quantitative agreement with experimental and direct numerical simulation data. These results indicate that one must first ensure that 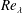$Re_{\unicode[STIX]{x1D706}}$ is large enough for the FRN effect to be negligibly small before the hypotheses of Kolmogorov (Dokl. Akad. Nauk SSSR, vol. 30, 1941a, pp. 301–305; Dokl. Akad. Nauk SSSR, vol. 32, 1941b, pp. 16–18; J. Fluid Mech., vol. 13, 1962, pp. 82–85) can be assessed unambiguously. An obvious implication is that results from experiments and direct numerical simulations for which 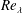$Re_{\unicode[STIX]{x1D706}}$ is well below 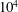$10^{4}$ may not be immune from the FRN effect. Another implication is that a power-law increase of 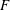$F$ with respect to 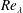$Re_{\unicode[STIX]{x1D706}}$, as suggested by the Kolmogorov 1962 theory, is not tenable when 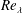$Re_{\unicode[STIX]{x1D706}}$ is large enough.

JFM classification

Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 856 , 10 December 2018 , pp. 426 - 443
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. & Burattini, P. 2006 Approach to the 4/5 law in homogeneous isotropic turbulence. J. Fluid Mech. 550, 175–184.Google Scholar
Antonia, R., Djenidi, L., Danaila, L. & Tang, S. 2017 Small scale turbulence and the finite Reynolds number effect. Phys. Fluids 29 (2), 020715.Google Scholar
Antonia, R., Tang, S. L., Djenidi, L. & Danaila, L. 2015 Boundedness of the velocity derivative skewness in various turbulent flows. J. Fluid Mech. 781, 727–744.Google Scholar
Batchelor, G. K. 1948 Energy decay and self-preserving correlation functions in isotropic turbulence. Q. Appl. Maths 6, 97–116.Google Scholar
Bos, W. J. T., Shao, L. & Bertoglio, J. P. 2007 Spectral imbalance and the normalized dissipation rate of turbulence. Phys. Fluids 19 (4), 045101.Google Scholar
Comte-Bellot, G. & Corrsin, S. 1966 The use of a contraction to improve the isotropy of grid-generated turbulence. J. Fluid Mech. 25, 657–682.Google Scholar
Danaila, L., Anselmet, F., Zhou, T. & Antonia, R. A. 1999 A generalization of Yaglom’s equation which accounts for the large-scale forcing in heated decaying turbulence. J. Fluid Mech. 391, 359–372.Google Scholar
Djenidi, L., Antonia, R. A., Talluru, M. K. & Abe, H. 2017a Skewness and flatness factors of the longitudinal velocity derivative in wall-bounded flows. Phys. Rev. Fluids 2 (6), 064608.Google Scholar
Djenidi, L., Danaila, L., Antonia, R. & Tang, S. 2017b A note on the velocity derivative flatness factor in decaying HIT. Phys. Fluids 29 (5), 051702.Google Scholar
Djenidi, L., Kamruzzaman, M. & Antonia, R. 2015 Power-law exponent in the transition period of decay in grid turbulence. J. Fluid Mech. 779, 544–555.Google Scholar
Djenidi, L., Lefeuvre, N., Kamruzzaman, M. & Antonia, R. 2017c On the normalized dissipation parameter C 𝜖 in decaying turbulence. J. Fluid Mech. 817, 61–79.Google Scholar
Grossmann, S. & Lohse, D. 1994 Scale resolved intermittency in turbulence. Phys. Fluids 6 (2), 611–617.Google Scholar
Hill, R. J. 2001 Equations relating structure functions of all orders. J. Fluid Mech. 434, 379–388.Google Scholar
Ishihara, T., Kaneda, Y., Yokokawa, M., Itakura, K. & Uno, A. 2007 Small-scale statistics in high-resolution direct numerical simulation of turbulence: Reynolds number dependence of one-point velocity gradient statistics. J. Fluid Mech. 592, 335–366.Google Scholar
Kolmogorov, A. N. 1941a The local structure of turbulence in incompressible viscous fluid for very large Reynolds number. Dokl. Akad. Nauk SSSR 30, 301–305; (see also Proc. R. Soc. Lond. A, 1991, 434, 9–13).Google Scholar
Kolmogorov, A. N. 1941b Dissipation of energy in the locally isotropic turbulence. Dokl. Akad. Nauk SSSR 32, 16–18; (see also Proc. R. Soc. Lond. A, 1991, 434, 15–17).Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.Google Scholar
Kraichnan, R. H. 1974 On Kolmogorov’s inertial-range theories. J. Fluid Mech. 62 (2), 305–330.Google Scholar
Kuo, A. & Corrsin, S. 1971 Experiments on internal intermittency and fine-structure distribution functions in fully turbulent fluid. J. Fluid Mech. 50 (2), 285–319.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Fluid mechanics: Vol. 6 of Course of Theoretical Physics, 2nd edn. Pergamon Press.Google Scholar
Lefeuvre, N., Djenidi, L. & Antonia, R. A. 2015 Decay of mean energy dissipation rate on the axis of a turbulent round jet. In Proceedings of the Ninth Symposium on Turbulence and Shear Flow Phenomena (TSFP-9), 30 June–3 July, Melbourne, http://www.tsfp-conference.org/proceedings/tsfp9-contents-of-volume-3.html.Google Scholar
Lesieur, M. 1997 Turbulence in Fluids, 3rd edn. Kluwer.Google Scholar
Lindborg, E. 1999 Correction to the four-fifths law due to variations of the dissipation. Phys. Fluids 11 (3), 510–512.Google Scholar
Lundgren, T. S. 2002 Kolmogorov two-thirds law by matched asymptotic expansion. Phys. Fluids 14 (2), 638–642.Google Scholar
McComb, W. D. 2014 Homogeneous, Isotropic Turbulence, Phenomenology, Renormalization and Statistical Closures. Oxford University Press.Google Scholar
Meldi, M. 2016 The signature of initial production mechanisms in isotropic turbulence decay. Phys. Fluids 28, 035105.Google Scholar
Meldi, M. & Sagaut, P. 2012 On non-self-similar regimes in homogeneous isotropic turbulence decay. J. Fluid Mech. 711, 364–393.Google Scholar
Meldi, M. & Sagaut, P. 2013a Further insights into self-similarity and self-preservation in freely decaying isotropic turbulence. J. Turbul. 14, 24–53.Google Scholar
Meldi, M. & Sagaut, P. 2013b Pressure statistics in self-similar freely decaying isotropic turbulence. J. Fluid Mech. 717, R2.Google Scholar
Meldi, M. & Sagaut, P. 2014 An adaptive numerical method for solving EDQNM equations for the analysis of long-time decay of isotropic turbulence. J. Comput. Phys. 262, 72–85.Google Scholar
Meldi, M. & Sagaut, P. 2017 Turbulence in a box: Quantification of large-scale resolution effects in isotropic turbulence free decay. J. Fluid Mech. 818, 697–715.Google Scholar
Meyers, J. & Meneveau, C. 2008 A functional form for the energy spectrum parametrizing bottleneck and intermittency effects. Phys. Fluids 20 (6), 065109.Google Scholar
Mydlarski, L. & Warhaft, Z. 1996 On the onset of high- Reynolds-number grid-generated wind tunnel turbulence. J. Fluid Mech. 320, 331–368.Google Scholar
Oboukhov, A. 1962 Some specific features of atmospheric turbulence. J. Fluid Mech. 13 (1), 77–81.Google Scholar
Orszag, S. A. 1970 Analytical theories of turbulence. J. Fluid Mech. 41, 363–386.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Qian, J. 1982 Variational approach to the closure problem of turbulence theory. Phys. Fluids 26 (8), 2098–2104.Google Scholar
Qian, J. 1986 A closure theory of intermittency of turbulence. Phys. Fluids 29 (7), 2165–2171.Google Scholar
Qian, J. 1994 Skewness factor of turbulent velocity derivative. Acta Mechanica Sin. 10, 12–15.Google Scholar
Qian, J. 1997 Inertial range and the finite Reynolds number effect of turbulence. Phys. Rev. E 55 (1), 337.Google Scholar
Qian, J. 1999 Slow decay of the finite Reynolds number effect of turbulence. Phys. Rev. E 60 (3), 3409.Google Scholar
Qian, J. 2000 Closure approach to high-order structure functions of turbulence. Phys. Rev. Lett. 84 (4), 646.Google Scholar
Saffman, P. J. 1967 The large-scale structure of homogeneous turbulence. J. Fluid Mech. 27, 581–593.Google Scholar
Sagaut, P. & Cambon, C. 2018 Homogenous Turbulence Dynamics. Springer.Google Scholar
Sreenivasan, K. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Tang, S., Antonia, R., Djenidi, L., Abe, H., Zhou, T., Danaila, L. & Zhou, Y. 2015a Transport equation for the mean turbulent energy dissipation rate on the centreline of a fully developed channel flow. J. Fluid Mech. 777, 151–177.Google Scholar
Tang, S., Antonia, R., Djenidi, L., Danaila, L. & Zhou, Y. 2017 Finite Reynolds number effect on the scaling range behaviour of turbulent longitudinal velocity structure functions. J. Fluid Mech. 820, 341–369.Google Scholar
Tang, S., Antonia, R., Djenidi, L., Danaila, L. & Zhou, Y. 2018 Reappraisal of the velocity derivative flatness factor in various turbulent flows. J. Fluid Mech. 847, 244–265.Google Scholar
Tang, S., Antonia, R., Djenidi, L. & Zhou, Y. 2015b Transport equation for the isotropic turbulent energy dissipation rate in the far-wake of a circular cylinder. J. Fluid Mech. 784, 109–129.Google Scholar
Tchoufag, J., Sagaut, P. & Cambon, C. 2012 Spectral approach to finite Reynolds number effects on Kolmogorovs 4/5 law in isotropic turbulence. Phys. Fluids 24 (1), 015107.Google Scholar
Valente, P. C. & Vassilicos, J. C. 2012 Dependence of decaying homogeneous isotropic turbulence on inflow conditions. Phys. Lett. A 376, 510–514.Google Scholar
Zhou, T., Antonia, R., Danaila, L. & Anselmet, F. 2000 Approach to the four-fifths ‘law’ for grid turbulence. J. Turbul. 1, N5.Google Scholar
Zhou, T., Antonia, R. A. & Chua, L. P. 2005 Flow and Reynolds number dependencies of one-dimensional vorticity fluctuations. J. Turbul. 6, 1–17.Google Scholar