Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-27T14:02:06.620Z Has data issue: false hasContentIssue false
  • English
  • Français

A revisit of the equilibrium assumption for predicting near-wall turbulence

Published online by Cambridge University Press:  07 November 2014

Farid Karimpour  and
Subhas K. Venayagamoorthy
Farid Karimpour
Affiliation:
Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, CO 80523-1372, USA
Subhas K. Venayagamoorthy*
Affiliation:
Department of Civil and Environmental Engineering, Colorado State University, Fort Collins, CO 80523-1372, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this study, we revisit the consequence of assuming equilibrium between the rates of production (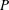$P$) and dissipation 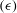$({\it\epsilon})$ of the turbulent kinetic energy 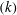$(k)$ in the highly anisotropic and inhomogeneous near-wall region. Analytical and dimensional arguments are made to determine the relevant scales inherent in the turbulent viscosity (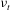${\it\nu}_{t}$) formulation of the standard 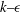$k{-}{\it\epsilon}$ model, which is one of the most widely used turbulence closure schemes. This turbulent viscosity formulation is developed by assuming equilibrium and use of the turbulent kinetic energy 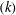$(k)$ to infer the relevant velocity scale. We show that such turbulent viscosity formulations are not suitable for modelling near-wall turbulence. Furthermore, we use the turbulent viscosity 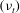$({\it\nu}_{t})$ formulation suggested by Durbin (Theor. Comput. Fluid Dyn., vol. 3, 1991, pp. 1–13) to highlight the appropriate scales that correctly capture the characteristic scales and behaviour of 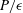$P/{\it\epsilon}$ in the near-wall region. We also show that the anisotropic Reynolds stress (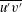$\overline{u^{\prime }v^{\prime }}$) is correlated with the wall-normal, isotropic Reynolds stress (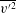$\overline{v^{\prime 2}}$) as 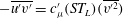$-\overline{u^{\prime }v^{\prime }}=c_{{\it\mu}}^{\prime }(ST_{L})(\overline{v^{\prime 2}})$, where 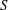$S$ is the mean shear rate, 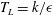$T_{L}=k/{\it\epsilon}$ is the turbulence (decay) time scale and 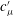$c_{{\it\mu}}^{\prime }$ is a universal constant. ‘A priori’ tests are performed to assess the validity of the propositions using the direct numerical simulation (DNS) data of unstratified channel flow of Hoyas & Jiménez (Phys. Fluids, vol. 18, 2006, 011702). The comparisons with the data are excellent and confirm our findings.

JFM classification

Turbulent Flows: Turbulence modelling Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 760 , 10 December 2014 , pp. 304 - 312
Check for updates
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Corrsin, S. 1958 Local isotropy in turbulent shear flow. NACA RM 58B11, 1–15.Google Scholar
Durbin, P. A. 1991 Near-wall turbulence closure modeling without damping functions. Theor. Comput. Fluid Dyn. 3, 1–13.Google Scholar
Durbin, P. A. & Pettersson Reif, B. A. 2011 Statistical Theory and Modeling for Turbulent Flows. John Wiley and Sons.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $\mathit{Re}_{{\it\tau}}=2003$ . Phys. Fluids 18, 011702.Google Scholar
Jiménez, J. 2013 How linear is wall-bounded turbulence? Phys. Fluids 25, 110814.Google Scholar
Jones, W. P. & Launder, B. E. 1973 The calculation of low-Reynolds-number phenomena with a two-equation model of turbulence. Intl J. Heat Mass Transfer 16, 1119–1130.Google Scholar
Karimpour, F. & Venayagamoorthy, S. K. 2013 Some insights for the prediction of near-wall turbulence. J. Fluid Mech. 723, 126–139.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177, 133–166.Google Scholar
Kolmogorov, A. N. 1942 Equations of turbulent motion of an incompressible fluid. Izv. Acad. Nauk, SSSR; Ser. Fiz. 6, 56–58.Google Scholar
Lam, C. K. G. & Bremhorst, K. A. 1981 A modified form of the $k{-}{\it\epsilon}$ model for predicting wall turbulence. Trans. ASME I: J. Fluids Engng 103, 456–460.Google Scholar
Launder, B. E. & Sharma, B. I. 1974 Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning disc. Lett. Heat Mass Transfer 1, 131–137.CrossRefGoogle Scholar
Launder, B. E. & Spalding, D. B. 1972 Mathematical Models of Turbulence. Academic Press.Google Scholar
Lumley, J. L. 1978 Computational modeling of turbulent flows. Adv. Appl. Mech. 18, 123–176.Google Scholar
Marusic, I. & Perry, A. E. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 2. Further experimental support. J. Fluid Mech. 298, 389–407.CrossRefGoogle Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to $\mathit{Re}_{{\it\tau}}=590$ . Phys. Fluids 11, 943–945.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Rodi, W. & Mansour, N. N. 1993 Low-Reynolds-number $k{-}{\it\epsilon}$ modelling with the aid of direct numerical simulation data. J. Fluid Mech. 250, 509–529.Google Scholar
Schultz, M. P. & Flack, K. A. 2013 Reynolds-number scaling of turbulent channel flow. Phys. Fluids 25, 025104.Google Scholar