Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-10T06:17:16.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Resonant sloshing in an upright annular tank

Published online by Cambridge University Press:  13 September 2016

Odd M. Faltinsen ,
Ivan A. Lukovsky  and
Alexander N. Timokha
Odd M. Faltinsen*
Affiliation:
Centre for Autonomous Marine Operations and Systems and Department of Marine Technology, Norwegian University of Science and Technology, NO-7491 Trondheim, Norway
Ivan A. Lukovsky
Affiliation:
Institute of Mathematics, National Academy of Sciences of Ukraine, 01601 Kiev, Ukraine
Alexander N. Timokha
Affiliation:
Centre for Autonomous Marine Operations and Systems and Department of Marine Technology, Norwegian University of Science and Technology, NO-7491 Trondheim, Norway Institute of Mathematics, National Academy of Sciences of Ukraine, 01601 Kiev, Ukraine
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

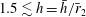Resonant sloshing in an upright annular tank is studied by using a new nonlinear modal theory, which is complete within the framework of the Narimanov–Moiseev asymptotics. The applicability is justified for a fairly deep liquid (the liquid-depth-to-outer-tank-radius ratio $1.5\lesssim h=\bar{h}/\bar{r}_{2}$) and away from the non-dimensional inner radii 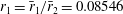$r_{1}=\bar{r}_{1}/\bar{r}_{2}=0.08546$, 0.17618, 0.27826, 0.31323, 0.31855, 0.43444, 0.46015, 0.48434, 0.68655, 0.70118. The theory is used to describe steady-state (stable and unstable) resonant waves due to a harmonic excitation with the forcing frequency close to the lowest natural sloshing frequency. We show that the surge-sway-pitch-roll excitation is always of either longitudinal or elliptic type. Existing experimental results on the horizontally excited steady-state wave regimes in an upright circular tank (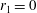$r_{1}=0$) are utilised for validation. Inserting an inner pole with the radii 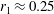$r_{1}\approx 0.25$ and 0.35 (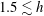$1.5\lesssim h$) causes that no stable swirling and/or irregular waves exist. The response curves for an elliptic-type excitation are examined versus the minor-axis forcing-amplitude component. Stable swirling is then expected being co- and counter-directed to the angular forcing direction. Passage to the rotary (circular) excitation keeps the co-directed swirling stable for all resonant forcing frequencies but the stable counter-directed swirling disappears.

JFM classification

Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 804 , 10 October 2016 , pp. 608 - 645
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramson, H. N.1966 The dynamic behavior of liquids in moving containers with applications to space vehicle technology. NASA Tech. Rep. SP-106. NASA, Washington.Google Scholar
Abramson, H. N., Chu, W.-H. & Kana, D. D.1966a Some studies of nonlinear lateral sloshing in rigid containers. NASA Contractor Rep. NASA CR-375. NASA.Google Scholar
Abramson, H. N., Chu, W. H. & Kana, D. D. 1966b Some studies of nonlinear lateral sloshing in rigid containers. J. Appl. Mech. 33 (4), 66–74.CrossRefGoogle Scholar
Aslam, M., Godden, W. G. & Scalise, D. T.1979 Sloshing of water in annular pressure-suppression pool of boiling water reactors under earthquake ground motions. Tech. Rep. NUREG/CR-1083; LBL-6754, TRN: 80-002028. California University, Berkeley (USA). Lawrence Berkeley Lab.CrossRefGoogle Scholar
Balendra, T., Ang, K. K., Paramasivam, P. & Lee, S. L. 1982 Free vibration analysis of cylindrical liquid storage tanks. Intl J. Mech. Sci. 24 (1), 47–59.Google Scholar
Bertelsen, A., Svardal, A. & Tjotta, S. 1973 Nonlinear streaming effects associated with oscillating cylinders. J. Fluid Mech. 59 (3), 493–511.Google Scholar
Bryant, P. J. 1989 Nonlinear progressive waves in a circular basin. J. Fluid Mech. 205, 453–467.Google Scholar
Chakrabarti, S. K. 1987 Hydrodynamics of Offshore Structures. WIT.Google Scholar
Chaplin, J. R. 1984 Nonlinear forces on a horizontal cylinder beneath waves. J. Fluid Mech. 147, 449–464.Google Scholar
Chu, W.-H. 1968 Subharmonic oscillations in an arbitrary tank resulting from axial excitation. Trans. ASME J. Appl. Mech. 35, 148–154.CrossRefGoogle Scholar
Faller, A. 2001 The constant-v vortex. J. Fluid Mech. 434, 167–180.Google Scholar
Faltinsen, O. M. 1990 Sea Loads on Ships and Offshore Structures. Cambridge University Press.Google Scholar
Faltinsen, O. M., Rognebakke, O. F. & Timokha, A. N. 2003 Resonant three-dimensional nonlinear sloshing in a square base basin. J. Fluid Mech. 487, 1–42.Google Scholar
Faltinsen, O. M., Rognebakke, O. F. & Timokha, A. N. 2006 Transient and steady-state amplitudes of resonant three-dimensional sloshing in a square base tank with a finite fluid depth. Phys. Fluids 18, 012103.Google Scholar
Faltinsen, O. M. & Timokha, A. N. 2009 Sloshing. Cambridge University Press.Google Scholar
Faltinsen, O. M. & Timokha, A. N. 2013 Multimodal analysis of weakly nonlinear sloshing in a spherical tank. J. Fluid Mech. 719, 129–164.Google Scholar
Fredriksson, D. W., Tsukrov, I. & Hudson, P. 2008 Engineering investigation of design procedures for closed containment marine aquaculture systems. Aquat. Engng 39, 91–102.CrossRefGoogle Scholar
Gavrilyuk, I., Lukovsky, I. & Timokha, A.N. 2000 A multimodal approach to nonlinear sloshing in a circular cylindrical tank. Hybrid Meth. Engng 2 (4), 463–483.Google Scholar
Gavrilyuk, I., Lukovsky, I., Trotsenko, Yu. & Timokha, A. 2007 Sloshing in a vertical circular cylindrical tank with an annular baffle. Part 2. Nonlinear resonant waves. J. Engng Maths 57, 57–78.CrossRefGoogle Scholar
Ghaemmaghami, A., Kianoush, R. & Yuan, Xian-Xun 2013 Numerical modeling of dynamic behavior of annular tuned liquid dampers for applications in wind towers. Comput.-Aided Civil Infrastructure Engng 28 (1), 38–51.Google Scholar
Hopfinger, E. J. & Baumbach, V. 2009 Liquid sloshing in cylindrical fuel tanks. Prog. Propul. Phys. 1, 279–292.Google Scholar
Hutton, R. E.1963 An investigation of nonlinear, nonplanar oscillations of fluid in cylindrical container. NASA Tech. Rep. NASA; D-1870.Google Scholar
Hutton, R. E. 1964 Fluid-particle motion during rotary sloshing. Trans. ASME J. Appl. Mech. 31 (1), 145–153.Google Scholar
Ibrahim, R. 2005 Liquid Sloshing Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Ibrahim, R. A. 2015 Recent advances in physics of fluid parametric sloshing and related problems. J. Fluids Engng 137, (ID 090801-1).Google Scholar
Ikeda, T., Harata, Y. & Osasa, T. 2016 Internal resonance of nonlinear sloshing in rectangular liquid tanks subjected to obliquely horizontal excitation. J. Sound Vib. 361, 210–225.Google Scholar
Lukovsky, I. A., Ovchynnykov, D. V. & Timokha, A. N. 2012 Asymptotic nonlinear multimodal method for liquid sloshing in an upright circular cylindrical tank. Part 1. Modal equations. Nonlinear Oscillations 14 (4), 512–525.Google Scholar
Lukovsky, I. A. & Timokha, A. N. 2011 Combining Narimanov–Moiseev’ and Lukovsky–Miles’ schemes for nonlinear liquid sloshing. J. Numer. Appl. Maths 105 (2), 69–82.Google Scholar
Lukovsky, I. & Timokha, A. 2015 Multimodal method in sloshing. Nonlinear Oscillations 18 (3), 295–312.Google Scholar
Lukovsky, I. A. 1990 Introduction to Nonlinear Dynamics of Rigid Bodies with the Cavities Partially Filled by a Fluid. Naukova Dumka.Google Scholar
Lukovsky, I. A. 2015 Nonlinear Dynamics: Mathematical Models for Rigid Bodies with a Liquid. De Gruyter.Google Scholar
Mikishev, G. N. & Rabinovich, B. I. 1968 Dynamics of a Solid Body with Cavities Partially Filled with Liquid. Mashinostroenie (in Russian).Google Scholar
Miles, J. W. 1984a Internally resonant surface waves in circular cylinder. J. Fluid Mech. 149, 1–14.Google Scholar
Miles, J. W. 1984b Resonantly forces surface waves in circular cylinder. J. Fluid Mech. 149, 15–31.Google Scholar
Miles, J. W.1956 On the sloshing of liquid in a cylindrical tank. Tech. Rep. Thompson RAMO Woolridge Inc., Los Angeles, CA.Google Scholar
Miles, J. W. 1967 Surface-wave damping in closed basins. Proc. R. Soc. Lond. A 297, 459–475.Google Scholar
Miles, J. W. & Henderson, D. M. 1998 A note on interior versus boundary-layer damping of surface waves in a circular cylinder. J. Fluid Mech. 364, 319–323.Google Scholar
Moiseev, N. N. 1958 On the theory of nonlinear vibrations of a liquid of finite volume. J. Appl. Math. Mech. 22 (5), 860–872.Google Scholar
Narimanov, G. S. 1957 Movement of a tank partly fllled by a fluid: the taking into account of non-smallness of amplitude. Prikl. Math. Mech. 21, 513–524.Google Scholar
Ostrogradsky, M.-A. 1832 Mémoire sur la propagation des ondes dans un bassin cylindrique. Mémoires a l’Academie Royale des Sciences, De l’Institut de France III, 23–44.Google Scholar
Pirhonen, J. & Forsman, L. 1998 Relationship between Na+,K+-atpase activity and migration behaviour of brown trout and sea trout (Salmo trutta L.) during the smolting period. Aquaculture 168 (1–4), 41–47.Google Scholar
Prandtl, L. 1949 Erzeugung von Zirkulation beim Schütteln von Gefässen. ZAMM 29 (1/2), 8–9.Google Scholar
Royon-Lebeaud, A., Hopfinger, E. J. & Cartellier, A. 2007 Liquid sloshing and wave breaking in circular and square-base cylindrical containers. J. Fluid Mech. 577, 467–494.Google Scholar
Schlichting, H. 1968 Boundary-layer Theory. McGraw-Hill.Google Scholar
Seydel, R. 2010 Practical Bifurcation and Stability Analysis, 3rd edn. Springer.CrossRefGoogle Scholar
Takahara, H. & Kimura, K. 2012 Frequency response of sloshing in an annular cylindrical tank subjected to pitching excitation. J. Sound Vib. 331 (13), 3199–3212.Google Scholar
Tedesco, J. W., Landis, D. W. & Kostem, C. N. 1989 Seismic analysis of cylindrical liquid storage tanks. Comput. Struct. 32 (5), 1165–1174.Google Scholar
Timmons, M. B., Summerfelt, S. T. & Vinci, B. J. 1998 Review of circular tank technology and management. Aquat. Engng 18, 51–69.Google Scholar
Turner, M. R., Bridges, T. J. & Ardakani, H. A. 2015 The pendulum-slosh problem: simulation using a time-dependent conformal mapping. J. Fluids Struct. 59, 202–223.CrossRefGoogle Scholar
Supplementary material: File

Faltinsen supplementary material

Faltinsen supplementary material 1

Download Faltinsen supplementary material(File)
File 87.3 KB