Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-20T06:51:55.811Z Has data issue: false hasContentIssue false
  • English
  • Français

Resonance patterns in spatially forced Rayleigh–Bénard convection

Published online by Cambridge University Press:  01 September 2014

S. Weiss ,
G. Seiden  and
E. Bodenschatz
S. Weiss*
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, D-37073 Göttingen, Germany
G. Seiden
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, D-37073 Göttingen, Germany
E. Bodenschatz
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, D-37073 Göttingen, Germany Department of Physics, Cornell University, Ithaca, NY 14853-2501, USA
*
†Present address: Department of Physics, University of California, Santa Barbara, CA 93106, USA. Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

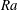We report on the influence of a quasi-one-dimensional periodic forcing on the pattern selection process in Rayleigh–Bénard convection (RBC). The forcing was introduced by a lithographically fabricated periodic texture on the bottom plate. We study the convection patterns as a function of the Rayleigh number ($\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Ra}$) and the dimensionless forcing wavenumber (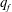$q_f$). For small $\mathit{Ra}$, convection takes the form of straight parallel rolls that are locked to the underlying forcing pattern. With increasing 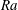$\mathit{Ra}$, these rolls give way to more complex patterns, due to a secondary instability. The forcing wavenumber 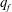$q_f$ was varied in the experiment over the range of 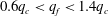$0.6q_c<q_f<1.4q_c$, with 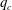$q_c$ being the critical wavenumber of the unforced system. We investigate the stability of straight rolls as a function of 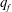$q_f$ and report patterns that arise due to a secondary instability.

JFM classification

Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Nonlinear Dynamical Systems: Pattern formation
Type
Papers
Information
Journal of Fluid Mechanics , Volume 756 , 10 October 2014 , pp. 293 - 308
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Department of Earth and Planetary Sciences, Faculty of Chemistry, Weizemann Institute of Science, Rehovot, Israel.

References

Berry, M. V. & Bodenschatz, E. 1999 Caustics, multiply reconstructed by talbot interference. J. Mod. Opt. 46 (2), 349–365.Google Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.Google Scholar
Boussinesq, J. 1903 Theorie Analytique de la Chaleur, vol. 2. Gauthier-Villars.Google Scholar
Brown, S. N. & Stewartson, K. 1978 On finite amplitude Benard convection in a cylindrical container. Proc. R. Soc. Lond. A 360 (1703), 455–469.Google Scholar
de Bruyn, J. R., Bodenschatz, E., Morris, S. W., Trainoff, S., Hu, Y., Cannell, D. S. & Ahlers, G. 1996 Apparatus for the study of Rayleigh–Bénard convection in gases under pressure. Rev. Sci. Instrum. 67, 2043–2067.Google Scholar
Busse, F. H. 1967 The stability of finite amplitude cellular convection and its relation to an extremum principle. J. Fluid Mech. 30, 625–649.CrossRefGoogle Scholar
Busse, F. H. 1978 Nonlinear properties of convection. Rep. Prog. Phys. 41, 1926–1967.CrossRefGoogle Scholar
Busse, F. H. & Whitehead, J. A. 1971 Instabilities of convection rolls in a high Prandtl number fluid. J. Fluid Mech. 47, 305–320.Google Scholar
Busse, F. H. & Whitehead, J. A. 1974 Oscillatory instabilities in large Prandtl number convection. J. Fluid Mech. 66, 67–79.CrossRefGoogle Scholar
Chen, M. M. & Whitehead, J. A. 1968 Evolution of two-dimensional periodic Rayleigh convection cells of arbitrary wavenumbers. J. Fluid Mech. 31, 1–15.Google Scholar
Cross, M. & Greenside, H. 2009 Pattern Formation and Dynamics in Nonequilibrium Systems. Cambridge University Press.Google Scholar
Cross, M. C. & Hohenberg, P. C. 1993 Pattern formation outside equilibrium. Rev. Mod. Phys. 65 (3), 851.Google Scholar
Freund, G., Pesch, W. & Zimmermann, W. 2011 Rayleigh–Bénard convection in the presence of spatial temperature modulations. J. Fluid Mech. 673, 318–348.Google Scholar
Hoyle, R. 2006 Pattern Formation – An Introduction to Methods. Cambridge University Press.Google Scholar
Kelly, R. E. & Pal, D. 1978 Thermal convection with spatially periodic boundary conditions: resonant wavelength excitation. J. Fluid Mech. 86, 433–456.Google Scholar
Kessler, M. A. & Werner, B. T. 2003 Self-organization of sorted patterned ground. Science 299, 380–383.CrossRefGoogle ScholarPubMed
Klausmeier, C. A. 1999 Regular and irregular patterns in semiarid vegetation. Science 284, 1826–1828.Google Scholar
Kuecken, M. & Newell, A. C. 2005 Fingerprint formation. J. Theor. Biol. 235, 71–83.Google Scholar
Lowe, M. & Gollub, J. P. 1985 Solitons and the commensurate–incommensurate transition in a convecting nematic fluid. Phys. Rev. A 31 (6), 3893–3897.Google Scholar
Lowe, M., Gollub, J. P. & Lubensky, T. C. 1983 Commensurate and incommensurate structures in a non-equilibrium system. Phys. Rev. Lett. 51 (9), 786–789.CrossRefGoogle Scholar
Luther, S., Fenton, F. H., Kornreich, B. G., Squires, A., Bittihn, P., Hornung, D., Zabel, M., Flanders, J., Gladuli, A., Campoy, L., Cherry, E. M., Luther, G., Hasenfuss, G., Krinsky, V. I., Pumir, A., Gilmour, R. F. Jr & Bodenschatz, E. 2011 Low-energy control of electrical turbulence in the heart. Nature 475, 235–239.Google Scholar
Manor, R., Hagberg, A. & Meron, E. 2008 Wavenumber locking in spatially forced pattern-forming systems. Europhys. Lett. 83, 10005 (p. 1–6).Google Scholar
Martin, C. P., Blunt, M. O., Pauliac-Vaujour, E., Stannard, A., Moriarty, P., Vancea, I. & Thiele, U. 2007 Controlling pattern formation in nanoparticle assemblies via directed solvent dewetting. Phys. Rev. Lett. 99 (11), 116103.Google Scholar
Mau, Y., Haim, L., Hagberg, A. & Meron, E. 2013 Competing resonances in spatially forced pattern-forming systems. Phys. Rev. E 88, 032917.Google Scholar
McCoy, J. H.2007 Adventures in pattern formation: spatially periodic forcing and self-organization. PhD thesis, Cornell University.Google Scholar
McCoy, J. H., Brunner, W., Pesch, W. & Bodenschatz, E. 2008 Self-organization of topological defects due to applied constraints. Phys. Rev. Lett. 101 (25), 254102.Google Scholar
Murray, J. D. 1989 Mathematical Biology. Springer.Google Scholar
Oberbeck, A. 1879 Über die Wärmeleitung der Flüssigkeiten bei Berücksichtigung der Strömungen infolge von Temperaturdifferenzen. Ann. Phys. Chem. 7, 271–292.CrossRefGoogle Scholar
Plapp, B. B.1997 Spiral pattern formation in Rayleigh–Bénard convection. PhD thesis, Cornell University.Google Scholar
Porter, J. & Silber, M. 2004 Resonant triad dynamics in weakly damped faraday waves with two-frequency forcing. Physica D 190 (1–2), 93–114.Google Scholar
Rasenat, S., Hartung, G., Winkler, B. L. & Rehberg, I. 1988 The shadowgraph method in convection experiments. Exp. Fluids 7, 412–420.Google Scholar
Rogers, J. L., Schatz, M. F., Brausch, O. & Pesch, W. 2000 Superlattice patterns in vertically oscillated Rayleigh–Bénard convection. Phys. Rev. Lett. 85 (20), 4281–4284.Google Scholar
Seiden, G., Weiss, S., McCoy, J., Pesch, W. & Bodenschatz, E. 2008 Pattern forming system in the presence of different symmetry-breaking mechanisms. Phys. Rev. Lett. 101, 214503.Google Scholar
Spiegel, E. A. & Veronis, G. 1960 On the Boussinesq approximation for a compressible fluid. Astrophys. J. 131, 442–447.Google Scholar
Stork, K. & Müller, U. 1975 Convection in boxes: an experimental investigation in vertical cylinders and annuli. J. Fluid Mech. 71, 231–240.Google Scholar
Taberlet, N., Morris, S. W. & McElwaine, J. N. 2007 Washboard road: the dynamics of granular ripples formed by rolling wheels. Phys. Rev. Lett. 99, 068003.Google Scholar
Tian, W., Parker, D. J. & Kilburn, C. A. D. 2003 Observation and numerical simulation of atmospheric cellular convection over mesoscale topography. Mon. Weath. Rev. 131, 222–235.Google Scholar
Trainoff, S. P. & Cannell, D. S. 2002 Physical optics treatment of the shadowgraph. Phys. Fluids 14, 1340–1363.CrossRefGoogle Scholar
Tschammer, A.1996 Nichtlineare Aspekte der Rayleigh–Bénard Konvektion in isotropen und anisotropen Fluiden. PhD thesis, Universität Bayreuth.Google Scholar
Turing, A. M. 1952 The chemical basis of morphogenesis. Phil. Trans. R. Soc. Lond. B 237 (641), 37–72.Google Scholar
Weiss, S.2009 Pattern formation in spatially forced thermal convection. PhD thesis, Georg-August-Universität Göttingen.Google Scholar
Weiss, S., Seiden, G. & Bodenschatz, E. 2012 Pattern formation in spatially forced thermal convection. New J. Phys. 14, 053010.CrossRefGoogle Scholar