Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-23T12:11:14.489Z Has data issue: false hasContentIssue false
  • English
  • Français

Relaminarization of spanwise-rotating viscoelastic plane Couette flow via a transition sequence from a drag-reduced inertial to a drag-enhanced elasto-inertial turbulent flow

Published online by Cambridge University Press:  01 December 2021

Yabiao Zhu Open the ORCID record for Yabiao Zhu [Opens in a new window] ,
Jiaxing Song Open the ORCID record for Jiaxing Song [Opens in a new window] ,
Fenghui Lin ,
Nansheng Liu Open the ORCID record for Nansheng Liu [Opens in a new window] ,
Xiyun Lu Open the ORCID record for Xiyun Lu [Opens in a new window]  and
Bamin Khomami
Yabiao Zhu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Jiaxing Song
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Fenghui Lin
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Nansheng Liu*
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Xiyun Lu
Affiliation:
Department of Modern Mechanics, University of Science and Technology of China, Hefei, Anhui 230026, PR China
Bamin Khomami*
Affiliation:
Department of Chemical and Biomolecular Engineering, University of Tennessee, Knoxville, TN 37996, USA
*
†Email addresses for correspondence: [email protected], [email protected]
†Email addresses for correspondence: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

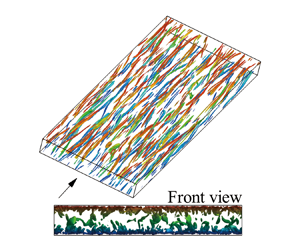
Direct numerical simulation of spanwise-rotation-driven flow transitions in viscoelastic plane Couette flow from a drag-reduced inertial to a drag-enhanced elasto-inertial turbulent flow state followed by full relaminarization is reported for the first time. Specifically, this novel flow transition begins with a drag-reduced inertial turbulent flow state at a low rotation number $0\leqslant Ro \leqslant 0.1$, and then transitions to a rotation/polymer-additive-driven drag-enhanced inertial turbulent regime, $0.1\leqslant Ro \leqslant 0.3$. In turn, the flow transitions to a drag-enhanced elasto-inertial turbulent state, $0.3\leqslant Ro \leqslant 0.9$, and eventually relaminarizes at $Ro=1$. In addition, two novel rotation-dependent drag enhancement mechanisms are proposed and substantiated. (1) The formation of large-scale roll cells results in enhanced convective momentum transport along with significant polymer elongation and stress generated in the extensionally dominated flow between adjacent roll cells at $Ro\leqslant 0.2$. (2) Coriolis-force-generated turbulent vortices cause strong incoherent transport and homogenization of significant polymer stress in the bulk via their vortical circulations at $Ro=0.5 - 0.9$.

JFM classification

Turbulent Flows: Rotating turbulence Non-Newtonian Flows: Viscoelasticity
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 931 , 25 January 2022 , R7
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bech, K.H. & Andersson, H.I. 1996 Secondary flow in weakly rotating turbulent plane Couette flow. J. Fluid Mech. 317, 195–214.CrossRefGoogle Scholar
Bech, K.H. & Andersson, H.I. 1997 Turbulent plane Couette flow subject to strong system rotation. J. Fluid Mech. 347, 289–314.CrossRefGoogle Scholar
Brauckmann, H.J., Salewski, M. & Eckhardt, B. 2016 Momentum transport in Taylor–Couette flow with vanishing curvature. J. Fluid Mech. 790, 419–452.CrossRefGoogle Scholar
Choueiri, G.H., Lopez, J.M. & Hof, B. 2018 Exceeding the asymptotic limit of polymer drag reduction. Phys. Rev. Lett. 120 (12), 124501.CrossRefGoogle ScholarPubMed
De Angelis, E., Casciola, C.M. & Piva, R. 2002 DNS of wall turbulence: dilute polymers and self-sustaining mechanisms. Comput. Fluids 31, 495–507.CrossRefGoogle Scholar
Dubief, Y., Terrapon, V.E. & Soria, J. 2013 On the mechanism of elasto-inertial turbulence. Phys. Fluids 25 (11), 110817.CrossRefGoogle ScholarPubMed
Dubief, Y., Terrapon, V.E., White, C.M., Shaqfeh, E.S., Moin, P. & Lele, S.K. 2005 New answers on the interaction between polymers and vortices in turbulent flows. Flow Turbul. Combust. 74, 311–329.CrossRefGoogle Scholar
Gai, J., Xia, Z., Cai, Q. & Chen, S. 2016 Turbulent statistics and flow structures in spanwise-rotating turbulent plane Couette flows. Phys. Rev. Fluids 1 (5), 054401.CrossRefGoogle Scholar
Kawata, T. & Alfredsson, P.H. 2016 Experiments in rotating plane Couette flow – momentum transport by coherent roll-cell structure and zero-absolute-vorticity state. J. Fluid Mech. 791, 191–213.CrossRefGoogle Scholar
Kim, K., Li, C.-F., Sureshkumar, R., Balachandar, S. & Adrian, R.J. 2007 Effects of polymer stresses on eddy structures in drag-reduced turbulent channel flow. J. Fluid Mech. 584, 281–299.CrossRefGoogle Scholar
Li, C.-F., Sureshkumar, R. & Khomami, B. 2006 Influence of rheological parameters on polymer induced turbulent drag reduction. J. Non-Newtonian Fluid Mech. 140 (1-3), 23–40.CrossRefGoogle Scholar
Li, C.-F., Sureshkumar, R. & Khomami, B. 2015 Simple framework for understanding the universality of the maximum drag reduction asymptote in turbulent flow of polymer solutions. Phys. Rev. E 92, 043014.CrossRefGoogle ScholarPubMed
Liu, N. & Khomami, B. 2013 a Elastically induced turbulence in Taylor–Couette flow: direct numerical simulation and mechanistic insight. J. Fluid Mech. 737, R4.CrossRefGoogle Scholar
Liu, N. & Khomami, B. 2013 b Polymer-induced drag enhancement in turbulent Taylor–Couette flows: direct numerical simulations and mechanistic insight. Phys. Rev. Lett. 111, 114501.CrossRefGoogle ScholarPubMed
Lopez, J.M., Choueiri, G.H. & Hof, B. 2019 Dynamics of viscoelastic pipe flow at low Reynolds numbers in the maximum drag reduction limit. J. Fluid Mech. 874, 699–719.CrossRefGoogle Scholar
Pereira, A.S., Mompean, G., Thais, L. & Soares, E.J. 2017 a Transient aspects of drag reducing plane Couette flows. J. Non-Newtonian Fluid Mech. 241, 60–69.CrossRefGoogle Scholar
Pereira, A.S., Mompean, G., Thais, L., Soares, E.J. & Thompson, R.L. 2017 b Active and hibernating turbulence in drag-reducing plane Couette flows. Phys. Rev. Fluids 2 (8), 084605.CrossRefGoogle Scholar
Salewski, M. & Eckhardt, B. 2015 Turbulent states in plane Couette flow with rotation. Phys. Fluids 27 (4), 045109.CrossRefGoogle Scholar
Samanta, D., Dubief, Y., Holzner, M., Schäfer, C., Morozov, A.N., Wagner, C. & Hof, B. 2013 Elasto-inertial turbulence. Proc. Natl Acad. Sci. USA 110 (26), 10557–10562.CrossRefGoogle ScholarPubMed
Shekar, A., McMullen, R.M., Wang, S.-N., McKeon, B.J. & Graham, M.D. 2019 Critical-layer structures and mechanisms in elastoinertial turbulence. Phys. Rev. Lett. 122 (12), 124503.CrossRefGoogle ScholarPubMed
Song, J., Teng, H., Liu, N., Ding, H., Lu, X. & Khomami, B. 2019 The correspondence between drag enhancement and vortical structures in turbulent Taylor–Couette flows with polymer additives: a study of curvature dependence. J. Fluid Mech. 881, 602–616.CrossRefGoogle Scholar
Teng, H., Liu, N., Lu, X. & Khomami, B. 2018 Turbulent drag reduction in plane Couette flow with polymer additives: a direct numerical simulation study. J. Fluid Mech. 846, 482–507.CrossRefGoogle Scholar
Toms, B.A. 1948 Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. In Proceedings of the International Congress on Rheology (ed. J.M. Burgers), pp. 135–141. North Holland.Google Scholar
Tsukahara, T., Tillmark, N. & Alfredsson, P.H. 2010 Flow regimes in a plane Couette flow with system rotation. J. Fluid Mech. 648, 5–33.CrossRefGoogle Scholar
Virk, P.S. 1975 Drag reduction fundamentals. AIChE J. 21 (4), 625–656.CrossRefGoogle Scholar
White, C.M. & Mungal, M.G. 2008 Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 40, 235–256.CrossRefGoogle Scholar
Xi, L. 2019 Turbulent drag reduction by polymer additives: fundamentals and recent advances. Phys. Fluids 31, 121302.Google Scholar
Xia, Z., Shi, Y., Wan, M., Sun, C., Cai, Q. & Chen, S. 2019 Role of the large-scale structures in spanwise rotating plane Couette flow with multiple states. Phys. Rev. Fluids 4 (10), 104606.CrossRefGoogle Scholar
Zhu, Y., Song, J., Liu, N., Lu, X. & Khomami, B. 2020 Polymer-induced flow relaminarization and drag enhancement in spanwise-rotating plane Couette flow. J. Fluid Mech. 905, A19.CrossRefGoogle Scholar