Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-20T00:50:34.407Z Has data issue: false hasContentIssue false
  • English
  • Français

Regular and complex singularities of the generalized thin film equation in two dimensions

Published online by Cambridge University Press:  23 April 2021

M.C. Dallaston ,
M.A. Fontelos ,
M.A. Herrada Open the ORCID record for M.A. Herrada [Opens in a new window] ,
J.M. Lopez-Herrera Open the ORCID record for J.M. Lopez-Herrera [Opens in a new window]  and
J. Eggers Open the ORCID record for J. Eggers [Opens in a new window]
M.C. Dallaston
Affiliation:
School of Mathematical Sciences, Queensland University of Technology, Brisbane, QLD4001, Australia
M.A. Fontelos
Affiliation:
Instituto de Ciencias Matemáticas, (ICMAT, CSIC-UAM-UCM-UC3M), Campus de Cantoblanco, 28049Madrid, Spain
M.A. Herrada
Affiliation:
E.S.I., Universidad de Sevilla, Camino de los Descubrimientos s/n, 41092, Spain
J.M. Lopez-Herrera
Affiliation:
E.S.I., Universidad de Sevilla, Camino de los Descubrimientos s/n, 41092, Spain
J. Eggers*
Affiliation:
School of Mathematics, University of Bristol, Fry Building, Woodland Road, BristolBS8 1UG, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

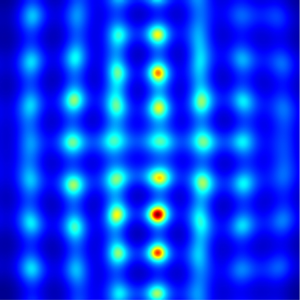
We use a generalized version of the equation of motion for a thin film of liquid on a solid, horizontal substrate as a model system to study the formation of singularities in space dimensions greater than one. Varying both the exponent controlling long-ranged forces, as well as the exponent of the nonlinear mobility, we predict the structure of the singularity as the film thickness goes to zero. The spatial structure of rupture may be either ‘pointlike’ (approaching axisymmetry) or ‘quasi-one-dimensional’, in which case a one-dimensional singularity is unfolded into two or higher space dimensions. The scaling of the profile with time may be either strictly self-similar (the ‘regular’ case) or discretely self-similar and perhaps chaotic (the ‘irregular’ case). We calculate the phase boundaries between these regimes, and confirm our results by detailed comparisons with time-dependent simulations of the nonlinear thin film equation in two space dimensions.

JFM classification

Interfacial Flows (free surface): Thin films Nonlinear Dynamical Systems: Pattern formation
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 917 , 25 June 2021 , A20
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Angenent, S.B., Aronson, D.G., Betelu, S.I. & Lowengrub, J.S. 2001 Focusing of an elongated hole in porous medium flow. Physica D 151, 228–252.CrossRefGoogle Scholar
Arnold, V.I. 1984 Catastrophe Theory. Springer.CrossRefGoogle Scholar
Aronson, D.G. 2016 The focusing problem for the porous medium equation: experiment, simulation and analysis. Nonlinear Anal. 137, 135–147.CrossRefGoogle Scholar
Becker, J. & Grün, G. 2005 The thin-film equation: recent advances and some new perspectives. J. Phys.: Condens. Matter 17, S291–S307.Google Scholar
Becker, J., Grün, G., Seemann, R., Mantz, H., Jacobs, K., Mecke, K.R. & Blossey, R. 2003 Complex dewetting scenarios captured by thin-film models. Nat. Mater. 2, 59–63.CrossRefGoogle ScholarPubMed
Benzaquen, M., Fowler, P., Jubin, L., Salez, T., Dalnoki-Veress, K. & Raphael, E. 2014 Approach to universal self-similar attractor for the levelling of thin liquid films. Soft Matt. 10, 8608–8614.CrossRefGoogle ScholarPubMed
Bernoff, A.J., Bertozzi, A.L. & Witelski, T.P. 1998 Axisymmetric surface diffusion: dynamics and stability of self-similar pinch-off. J. Stat. Phys. 93, 725–776.CrossRefGoogle Scholar
Bertozzi, A.L. & Pugh, M.C. 1994 The lubrication approximation for thin viscous films: the moving contact line with a ‘porous media’ cut off of van der Waals interactions. Nonlinearity 7, 1535–1564.CrossRefGoogle Scholar
Blossey, R. 2012 Thin Liquid Films. Springer.Google Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81, 739–805.Google Scholar
Chen, Y.-J. & Steen, P.H. 1997 Dynamics of inviscid capillary breakup: collapse and pinchoff of a film bridge. J. Fluid Mech. 341, 245–267.CrossRefGoogle Scholar
Choptuik, M.W. 1993 Universality and scaling in gravitational collapse of a massless scalar field. Phys. Rev. Lett. 70, 9–12.CrossRefGoogle ScholarPubMed
Cohen, I., Brenner, M.P., Eggers, J. & Nagel, S.R. 1999 Two fluid drop snap-off problem: experiment and theory. Phys. Rev. Lett. 83, 1147–1150.CrossRefGoogle Scholar
Constantin, P., Dupont, T.F., Goldstein, R.E., Kadanoff, L.P., Shelley, M.J. & Zhou, S.-M. 1993 Droplet breakup in a model of the Hele-Shaw cell. Phys. Rev. E 47, 4169–4181.CrossRefGoogle Scholar
Craster, R.V. & Matar, O.K. 2009 Dynamics and stability of thin liquid films. Rev. Mod. Phys. 81, 1131–1198.CrossRefGoogle Scholar
Dallaston, M.C, Tseluiko, D. & Kalliadasis, S. 2016 Dynamics of a thin film flowing down a heated wall with finite thermal diffusivity. Phys. Rev. Fluids 1, 073903.CrossRefGoogle Scholar
Dallaston, M.C., Fontelos, M.A., Tseluiko, D. & Kalliadasis, S. 2018 Discrete self-similarity in interfacial hydrodynamics and the formation of iterated structures. Phys. Rev. Lett. 120, 034505.CrossRefGoogle ScholarPubMed
Dallaston, M.C., Tseluiko, D., Zheng, Z., Fontelos, M.A. & Kalliadasis, S. 2017 Self-similar finite- time singularity formation in degenerate parabolic equations arising in thin-film flows. Nonlinearity 30, 2647–2666.CrossRefGoogle Scholar
Day, R.F., Hinch, E.J. & Lister, J.R. 1998 Self-similar capillary pinchoff of an inviscid fluid. Phys. Rev. Lett. 80, 704–707.CrossRefGoogle Scholar
de Gennes, P.-G. 1985 Wetting: statics and dynamics. Rev. Mod. Phys. 57, 827–863.CrossRefGoogle Scholar
Drazin, P.G. 1992 Nonlinear Systems. Cambridge University Press.CrossRefGoogle Scholar
Eggers, J. 1993 Universal pinching of 3D axisymmetric free-surface flow. Phys. Rev. Lett. 71, 3458–3460.Google ScholarPubMed
Eggers, J. 2012 Stability of a viscous pinching thread. Phys. Fluids 24, 072103.CrossRefGoogle Scholar
Eggers, J. 2018 The role of singularities in hydrodynamics. Phys. Rev. Fluids 3, 110503.CrossRefGoogle Scholar
Eggers, J. 2020 Self-similar structure of optical caustics, unpublished.Google Scholar
Eggers, J. & Fontelos, M.A. 2009 The role of self-similarity in singularities of partial differential equations. Nonlinearity 22, R1–R44.CrossRefGoogle Scholar
Eggers, J. & Fontelos, M.A. 2015 Singularities: Formation, Structure, and Propagation. Cambridge University Press.CrossRefGoogle Scholar
Eggers, J., Grava, T., Herrada, M.A. & Pitton, G. 2017 Spatial structure of shock formation. J. Fluid Mech. 820, 208–231.Google Scholar
Eggers, J., Herrada, M.A. & Snoeijer, J.H. 2020 Self-similar breakup of polymeric threads as described by the oldroyd-b model. J. Fluid Mech. 887, A19.CrossRefGoogle Scholar
Eggers, J., Hoppe, J., Hynek, M. & Suramlishvili, N. 2015 Singularities of relativistic membranes. Geom. Flows 1, 17–33.Google Scholar
Fontelos, M.A. & Wang, Q. 2021 Discrete selfsimilarity in the formation of satellites for viscous cavity break-up. Phys. Rev. Fluids 6, 013201.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence. Cambridge University Press.CrossRefGoogle Scholar
Giga, Y. & Kohn, R.V. 1985 Asymptotically self-similar blow-up of seminlinear heat-equations. Commun. Pure Appl. Maths 38, 297–319.CrossRefGoogle Scholar
Grauer, R. & Sideris, T.C. 1991 Numerical computation of 3d incompressible ideal fluids with swirl. Phys. Rev. Lett. 67, 3511–3514.CrossRefGoogle ScholarPubMed
Grava, T., Eggers, J. & Klein, C. 2016 Shock formation in the dispersionless Kadomtsev–Petviashvili equation. Nonlinearity 29, 1384–1416.CrossRefGoogle Scholar
Halsey, T.C., Jensen, M.H., Kadanoff, L.P., Procaccia, I. & Shraiman, B.I. 1986 Fractal measures and their singularities: the characterization of strange sets. Phys. Rev. E 33, 1141–1151.CrossRefGoogle ScholarPubMed
Herrada, M.A. & Montanero, J.M. 2016 A numerical method to study the dynamics of capillary fluid systems. J. Comput. Phys. 306, 137–147.CrossRefGoogle Scholar
Kuznetsov, Y.A. 2013 Elements of Applied Bifurcation Theory, vol. 112. Springer Science & Business Media.Google Scholar
Lin, T.-S., Rogers, S., Tseluiko, D. & Thiele, U. 2016 Bifurcation analysis of the behavior of partially wetting liquids on a rotating cylinder. Phys. Fluids 28, 082102.CrossRefGoogle Scholar
Münch, A., Wagner, B. & Witelski, T.P. 2005 Lubrication models with small slip lengths. J. Engng Maths 53, 359–383.CrossRefGoogle Scholar
Nore, C., Abid, M. & Brachet, M.-E. 1997 Kolmogorov turbulence in low-temperature superflows. Phys. Rev. Lett. 78, 3896–3899.CrossRefGoogle Scholar
Nye, J. 1999 Natural Focusing and Fine Structure of Light: Caustics and Wave Dislocations. Institute of Physics Publishing.Google Scholar
Oron, A. 2000 Nonlinear dynamics of three-dimensional long-wave Marangoni instability in thin liquid films. Phys. Fluids 12, 1633–1645.CrossRefGoogle Scholar
Oron, A., Davis, S.H. & Bankoff, S.G. 1997 Long-scale evolution of thin liquid films. Rev. Mod. Phys. 69, 931–980.CrossRefGoogle Scholar
Pomeau, Y., Le Berre, M., Guyenne, P. & Grilli, S. 2008 Wave-breaking and generic singularities of nonlinear hyperbolic equations. Nonlinearity 21, T61–T79.CrossRefGoogle Scholar
Popinet, S. 2015 Basilisk c libraries. Last accessed on 2020-07-20.Google Scholar
Pumir, A., Shraiman, B.I. & Siggia, E.D. 1992 Vortex morphology and Kelvin's theorem. Phys. Rev. A 45, R5351–R5354.CrossRefGoogle ScholarPubMed
Sharma, A., Kishore, C.S., Salaniwal, S. & Ruckenstein, E. 1995 Nonlinear stability and rupture of ultrathin free films. Phys. Fluids 7, 1832–1840.CrossRefGoogle Scholar
Sharma, A. & Verma, R. 2004 Pattern formation and dewetting in thin films of liquids showing complete macroscale wetting: from ‘pancakes’ to “swiss cheese”. Langmuir 20, 10337–10345.Google Scholar
Thiele, U. & Knobloch, E. 2003 Front and back instability of a liquid film on a slightly inclined plate. Phys. Fluids 15, 892–907.CrossRefGoogle Scholar
Thiele, U. & Knobloch, E. 2004 Thin liquid films on a slightly inclined heated plate. Physica D 190, 213–248.CrossRefGoogle Scholar
Tseluiko, D., Alesemi, M., Lin, T.-S. & Thiele, U. 2020 Effect of driving on coarsening dynamics in phase-separating systems. Nonlinearity 33, 4449–4483.CrossRefGoogle Scholar
Tseluiko, D., Baxter, J. & Thiele, U. 2013 A homotopy continuation approach for analysing finite-time singularities in thin liquid films. IMA J. Appl. Maths 78, 762–776.CrossRefGoogle Scholar
Williams, M.B. & Davis, S.H. 1982 Nonlinear theory of film rupture. J. Colloid Interfacs Sci. 90, 220–228.CrossRefGoogle Scholar
Witelski, T.P. & Bernoff, A.J. 1999 Stability of self-similar solutions for van der Waals driven thin film rupture. Phys. Fluids 11, 2443–2445.CrossRefGoogle Scholar
Witelski, T.P. & Bernoff, A.J. 2000 Dynamics of three-dimensional thin film rupture. Physica D 147, 155–176.CrossRefGoogle Scholar
Witelski, T.P. & Bowen, M. 2003 ADI schemes for higher-order nonlinear diffusion equations. Appl. Numer. Maths 45, 331–351.Google Scholar
Zhang, W.W. & Lister, J.R. 1999 a Similarity solutions for capillary pinch-off in fluids of differing viscosity. Phys. Rev. Lett. 83, 1151–1154.CrossRefGoogle Scholar
Zhang, W.W. & Lister, J.R. 1999 b Similarity solutions for van der Waals rupture of thin film on a solid substrate. Phys. Fluids 11, 2454–2462.CrossRefGoogle Scholar

Dallaston et al. supplementary movie

Time evolution of the inverse thickness as in Fig.12

Download Dallaston et al. supplementary movie(Video)
Video 1 MB