Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-20T00:13:44.271Z Has data issue: false hasContentIssue false
  • English
  • Français

Regime transitions and energetics of sustained stratified shear flows

Published online by Cambridge University Press:  22 July 2019

Adrien Lefauve Open the ORCID record for Adrien Lefauve [Opens in a new window] ,
J. L. Partridge  and
P. F. Linden
Adrien Lefauve*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
J. L. Partridge
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
P. F. Linden
Affiliation:
Department of Applied Mathematics and Theoretical Physics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe the long-term dynamics of sustained stratified shear flows in the laboratory. The stratified inclined duct (SID) experiment sets up a two-layer exchange flow in an inclined duct connecting two reservoirs containing salt solutions of different densities. This flow is primarily characterised by two non-dimensional parameters: the tilt angle of the duct with respect to the horizontal, 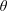$\unicode[STIX]{x1D703}$ (a few degrees at most), and the Reynolds number 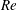$Re$, an input parameter based on the density difference driving the flow. The flow can be sustained with constant forcing over arbitrarily long times and exhibits a wealth of dynamical behaviours representative of geophysically relevant sustained stratified shear flows. Varying 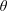$\unicode[STIX]{x1D703}$ and 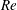$Re$ leads to four qualitatively different regimes: laminar flow; mostly laminar flow with finite-amplitude, travelling Holmboe waves; spatio-temporally intermittent turbulence with substantial interfacial mixing; and sustained, vigorous interfacial turbulence (Meyer & Linden, J. Fluid Mech., vol. 753, 2014, pp. 242–253). We seek to explain the scaling of the transitions between flow regimes in the two-dimensional plane of input parameters $(\unicode[STIX]{x1D703},Re)$. We improve upon previous studies of this problem by providing a firm physical basis and non-dimensional scaling laws that are mutually consistent and in good agreement with the empirical transition curves we inferred from 360 experiments spanning 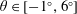$\unicode[STIX]{x1D703}\in [-1^{\circ },6^{\circ }]$ and 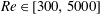$Re\in [300,5000]$. To do so, we employ state-of-the-art simultaneous volumetric measurements of the density field and the three-component velocity field, and analyse these experimental data using time- and volume-averaged potential and kinetic energy budgets. We show that regime transitions are caused by an increase in the non-dimensional time- and volume-averaged kinetic energy dissipation within the duct, which scales with 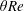$\unicode[STIX]{x1D703}Re$ at high enough angles. As the power input scaling with 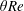$\unicode[STIX]{x1D703}Re$ is increased above zero, the two-dimensional, parallel-flow dissipation (power output) increases to close the budget through an increase in the magnitude of the exchange flow, incidentally triggering Holmboe waves above a certain threshold in interfacial shear. However, once the hydraulic limit of two-layer exchange flows is reached, two-dimensional dissipation plateaus and three-dimensional dissipation at small scales (turbulence) takes over, at first intermittently, and then steadily, in order to close the budget and follow the 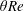$\unicode[STIX]{x1D703}Re$ scaling. This general understanding of regime transitions and energetics in the SID experiment may serve as a basis for the study of more complex sustained stratified shear flows found in the natural environment.

JFM classification

Geophysical and Geological Flows: Stratified flows Turbulent Flows: Stratified turbulence Turbulent Flows: Turbulent transition
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 875 , 25 September 2019 , pp. 657 - 698
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Armi, L. 1986 The hydraulics of two flowing layers with different densities. J. Fluid Mech. 163, 27–58.Google Scholar
Armi, L. & Farmer, D. M. 1988 The flow of Mediterranean water through the Strait of Gibraltar. Prog. Oceanogr. 21, 1–105.Google Scholar
Bartello, P. & Tobias, S. M. 2013 Sensitivity of stratified turbulence to the buoyancy Reynolds number. J. Fluid Mech. 725, 1–22.Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Caulfield, C. P. & Peltier, W. R. 2000 The anatomy of the mixing transition in homogeneous and stratified free shear layers. J. Fluid Mech. 413, 1–47.Google Scholar
Farmer, D. & Armi, L. 1999 Stratified flow over topography: the role of small-scale entrainment and mixing. Proc. R. Soc. Math., Phys. Engng Sci. 455, 3221–3258.Google Scholar
Fernando, H. J. S. 1991 Turbulent mixing in stratified fluids. Annu. Rev. Fluid Mech. 23 (1), 455–493.Google Scholar
Geyer, W. R., Lavery, A. C., Scully, M. E. & Trowbridge, J. H. 2010 Mixing by shear instability at high Reynolds number. Geophys. Res. Lett. 37 (22), L22607.Google Scholar
Gibson, C. H. 1980 Fossil temperature, salinity, and vorticity turbulence in the ocean. In Marine Turbulence (ed. Nihoul, J.), pp. 221–257. Elsevier.Google Scholar
Gregg, M. C., D’Asaro, E. A., Riley, J. J. & Kunze, E. 2018 Mixing efficiency in the ocean. Annu. Rev. Mar. Sci. (10), 443–473.Google Scholar
Gregg, M. C., Peters, H., Wesson, J. C., Oakey, N. S. & Shaw, T. J. 1985 Intensive measurements of turbulence and shear in the equatorial undercurrent. Nature 318, 140–144.Google Scholar
Gu, L.2001 Frictional exchange flow through a wide channel with application to the Burlington ship canal. PhD thesis, The University of British Columbia.Google Scholar
Gu, L. & Lawrence, G. A. 2005 Analytical solution for maximal frictional two-layer exchange flow. J. Fluid Mech. 543, 1–17.Google Scholar
van Haren, H., Gostiaux, L., Morozov, E. & Tarakanov, R. 2014 Extremely long Kelvin–Helmholtz billow trains in the Romanche Fracture Zone. Geophys. Res. Lett. 41 (23), 8445–8451.Google Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40 (1), 169–184.Google Scholar
Kiel, D. E.1991 Buoyancy driven counterflow and interfacial mixing. PhD thesis, University of Cambridge.Google Scholar
Lawrence, G. A. 1990 On the hydraulics of Boussinesq and non-Boussinesq two-layer flows. J. Fluid Mech. 215, 457–480.Google Scholar
Lefauve, A.2018 Waves and turbulence in sustained stratified shear flows. PhD thesis, University of Cambridge. doi:10.17863/CAM.24648.Google Scholar
Lefauve, A., Partridge, J. L., Zhou, Q., Caulfield, C. P., Dalziel, S. B. & Linden, P. F. 2018 The structure and origin of confined Holmboe waves. J. Fluid Mech. 848, 508–544.Google Scholar
Linden, P. F. 1979 Mixing in stratified fluids. Geophys. Astrophys. Fluid Dyn. 13 (1), 3–23.Google Scholar
Macagno, E. O. & Rouse, H. 1961 Interfacial mixing in stratified flow. J. Engng Mech. ASCE 87 (EM5), 55–81.Google Scholar
Mahrt, L. 2014 Stably stratified atmospheric boundary layers. Annu. Rev. Fluid Mech. 46 (1), 23–45.Google Scholar
Mashayek, A., Caulfield, C. P. & Peltier, W. R. 2013 Time-dependent, non-monotonic mixing in stratified turbulent shear flows: implications for oceanographic estimates of buoyancy flux. J. Fluid Mech. 736, 570–593.Google Scholar
Mashayek, A. & Peltier, W. R. 2012a The ‘zoo’ of secondary instabilities precursory to stratified shear flow transition. Part 1. Shear aligned convection, pairing, and braid instabilities. J. Fluid Mech. 708, 5–44.Google Scholar
Mashayek, A. & Peltier, W. R. 2012b The ‘zoo’ of secondary instabilities precursory to stratified shear flow transition. Part 2. The influence of stratification. J. Fluid Mech. 708, 45–70.Google Scholar
Meyer, C. R. & Linden, P. F. 2014 Stratified shear flow: experiments in an inclined duct. J. Fluid Mech. 753, 242–253.Google Scholar
Partridge, J. L., Lefauve, A. & Dalziel, S. B. 2019 A versatile scanning method for volumetric measurements of velocity and density fields. Meas. Sci. Technol. 30, 055203.Google Scholar
Peltier, W. R. & Caulfield, C. P. 2003 Mixing efficiency in stratified shear flows. Annu. Rev. Fluid Mech. 35 (1), 135–167.Google Scholar
Salehipour, H., Peltier, W. R. & Mashayek, A. 2015 Turbulent diapycnal mixing in stratified shear flows: the influence of Prandtl number on mixing efficiency and transition at high Reynolds number. J. Fluid Mech. 773, 178–223.Google Scholar
Schijf, J. B. & Schönfled, J. C. 1953 Theoretical considerations on the motion of salt and fresh water. In Proceedings of the Minnesota International Hydraulic Convention. IAHR.Google Scholar
de Silva, C. M., Philip, J. & Marusic, I. 2013 Minimization of divergence error in volumetric velocity measurements and implications for turbulence statistics. Exp. Fluids 54, 1557.Google Scholar
Smyth, W. D. & Moum, J. N. 2000 Length scales of turbulence in stably stratified mixing layers. Phys. Fluids 12 (6), 1327–1342.Google Scholar
Smyth, W. D. & Moum, J. N. 2013 Marginal instability and deep cycle turbulence in the eastern equatorial Pacific Ocean. Geophys. Res. Lett. 40 (23), 6181–6185.Google Scholar
Thorpe, S. A. & Liu, Z. 2009 Marginal instability? J. Phys. Oceanogr. 39 (9), 2373–2381.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Wang, C., Gao, Q., Wei, R., Li, T. & Wang, J. 2017 Weighted divergence correction scheme and its fast implementation. Exp. Fluids 58, 44.Google Scholar
Wilkinson, D. L. 1986 Buoyancy driven exchange flow in a horizontal pipe. J. Engng Mech. 112 (5), 485–497.Google Scholar
Winters, K. B., Lombard, P. N., Riley, J. J. & D’Asaro, E. A. 1995 Available potential energy and mixing in density-stratified fluids. J. Fluid Mech. 289, 115–128.Google Scholar